三、搜索与图论

news2024/11/19 0:32:39

DFS

排列数字

在这里插入图片描述

#include<iostream>
using namespace std;
const int N = 10;
int a[N], b[N];
int n;

void dfs(int u){
    if(u > n){
        for(int i = 1; i <= n; i++)
            cout<<a[i]<<" ";
        cout<<endl;
        return;
    }
    for(int i = 1; i <= n; i++){
        if(!b[i]){
            b[i] = 1;
            a[u] = i;
            dfs(u + 1);
            b[i] = 0;
        }
    }
}

int main(){
    cin>>n;
    dfs(1);
    return 0;
}

n-皇后问题

在这里插入图片描述

#include<iostream>
using namespace std;
const int N = 20;
char g[N][N];
int a[N], b[N], c[N];
int n;

void dfs(int u){
    if(u > n){
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= n; j++)
                cout<<g[i][j];
            cout<<endl;
        }
        cout<<endl;
        return;
    }
    for(int i = 1; i <= n; i++){
        if(!a[i] && !b[u + i] && !c[-u + i + n]){
            a[i] = b[u + i] = c[-u + i + n] = 1;
            g[u][i] = 'Q';
            dfs(u + 1);
            g[u][i] = '.';
            a[i] = b[u + i] = c[-u + i + n] = 0;
        }
    }
}

int main(){
    cin>>n;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            g[i][j] = '.';
    dfs(1);
    return 0;
}

BFS

走迷宫

在这里插入图片描述

#include<iostream>
#include<cstring>
using namespace std;
const int N = 110;
int g[N][N], d[N][N];
pair<int, int> q[N * N];
int hh, tt = - 1;
int n, m;

int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};

void bfs(int x, int y){
    memset(d, -1, sizeof(d));
    q[++tt] = make_pair(x, y);
    d[x][y] = 0;
    while(hh <= tt){
        auto t = q[hh++];
        for(int i = 0; i < 4; i++){
            int a = dx[i] + t.first, b = dy[i] + t.second;
            if(a < 1 || a > n || b < 1 || b > m) continue;
            if(d[a][b] != -1) continue;
            if(g[a][b] != 0) continue;
            d[a][b] = d[t.first][t.second] + 1;
            q[++tt] = make_pair(a, b);
        }
    }
    cout<<d[n][m];
}

int main(){
    cin>>n>>m;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            cin>>g[i][j];
    bfs(1, 1);
    return 0;
}

八数码

在这里插入图片描述
在这里插入图片描述

#include<iostream>
#include<unordered_map>
using namespace std;
const int N = 1e6; //一共有9!种情况
unordered_map<string, int> d;
string q[N];
int hh, tt = -1;
int n = 9;

int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};

int bfs(string s){
    q[++tt] = s;
    d[s] = 0;
    //记录终点
    string end = "12345678x";
    while(hh <= tt){
        string t = q[hh++];
        //存储当前位置到起点的距离
        int dis = d[t];
        //如果到终点了，那就返回距起点距离
        if(t == end) return dis;
        //查找x的下标
        int k = t.find('x');
        //x在矩阵中的位置
        int x = k / 3, y = k % 3;
        for(int i = 0; i < 4; i++){
            int a = x + dx[i], b = y + dy[i];
            if(a < 0 || a > 2 || b < 0 || b > 2) continue;
            //转移x
            swap(t[k], t[3 * a + b]);
            //如果没有遍历过，那就存储到队列中
            if(!d.count(t)){
                d[t] = dis + 1;
                q[++tt] = t;
            }
            //还原
            swap(t[k], t[3 * a + b]);
        }
    }
    return -1;
}

int main(){
    char c;
    string s = "";
    for(int i = 0; i < n; i++){
        cin>>c;
        s += c;
    }
    cout<<bfs(s);
    return 0;
}

树和图的存储

树是一种特殊的图
存储可以用链式向前星或者vector

//链式向前星
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[N], ne[N], idx;
int st[N];

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
}

void dfs(int u){
    st[u] = 1;
    for(int i = u; i != -1; i = ne[i]){
        int j = e[i];
        if(!st[j]) dfs(j);
    }
}

int main(){
    memset(h, -1, sizeof(h));
    return 0;
}

//vector存储
#include<iostream>
#include<vector>
using namespace std;
const int N = 1e5 + 10;
vector<int> v[N];
int st[N];

void add(int a, int b){
    v[a].push_back(b);
    v[b].push_back(a);
}

void dfs(int u){
    st[u] = 1;
    for(int i = 0; i < v[u].size(); i++){
        int j = v[u][i];
        if(!st[j]) dfs(j);
    }
}

int main(){
    return 0;
}

树与图的深度优先遍历

树的重心

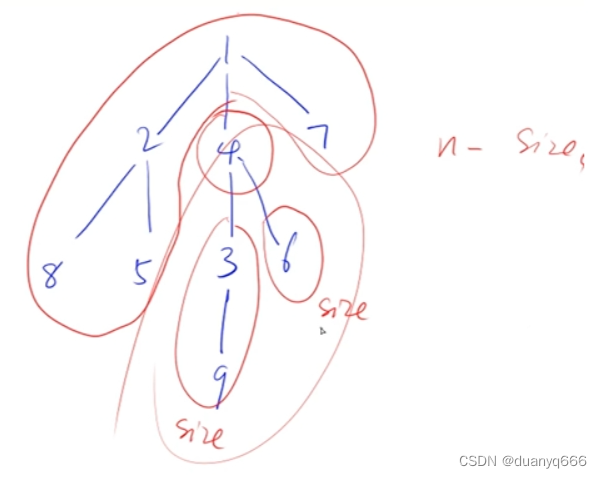
在这里插入图片描述
在这里插入图片描述

#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], idx;
int st[N];
int n, ans = 1e9;

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
}

int dfs(int u){
    st[u] = 1;
    //cnt存储以u为根的节点数（包括u），res是删除掉某个节点后的最大连通子图节点数
    int cnt = 1, res = 0; 
    for(int i = h[u]; i != -1; i = ne[i]){
        int j = e[i];
        if(!st[j]){
            //以u为节点的单棵子树的节点数
            int t = dfs(j);
            //计算以j为根的树的节点数
            cnt += t;
            //记录最大连通子图节点数
            res = max(res, t);
        }
    }
    //以u为重心，最大的连通子图节点数
    res = max(res, n - cnt);
    ans = min(ans, res);
    return cnt;
}

int main(){
    memset(h, -1, sizeof(h));
    cin>>n;
    int a, b;
    for(int i = 0; i < n - 1; i++){
        cin>>a>>b;
        add(a, b);
        add(b, a);
    }
    dfs(1);
    cout<<ans;
    return 0;
}

树与图的宽度优先遍历

图中点的层次

在这里插入图片描述

#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], idx;
int q[N], d[N], hh, tt = -1;
int n, m;

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
}

void bfs(int u){
    memset(d, -1, sizeof(d));
    q[++tt] = u;
    d[u] = 0;
    while(hh <= tt){
        //使用队头，弹出队头
        int t = q[hh++];
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            if(d[j] == -1){
                //更新距离
                d[j] = d[t] + 1;
                //入队
                q[++tt] = j;
            }
        }
    }
    cout<<d[n];
}

int main(){
    memset(h, -1, sizeof(h));
    cin>>n>>m;
    int x, y;
    while(m--){
        cin>>x>>y;
        add(x, y);
    }
    bfs(1);
    return 0;
}

拓扑排序

有向无环图也是拓扑图
入度：有多少条边指向自己
出度：有多少条边出去

有向图的拓扑序列

在这里插入图片描述
入度为0就是起点，出度为0就是终点

#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int q[N], hh, tt = -1;
int n, m;
int r[N]; //存储入度

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
}

void bfs(){
    //判断哪些点入度为0
    for(int i = 1; i <= n; i++)
        if(!r[i]) q[++tt] = i;
    while(hh <= tt){
        int t = q[hh++];
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            r[j]--;
            if(!r[j]) q[++tt] = j;
        }
    }
    if(tt == n - 1){
        for(int i = 0; i <= tt; i++) cout<<q[i]<<" ";
    }else cout<<-1;
}

int main(){
    memset(h, -1, sizeof(h));
    cin>>n>>m;
    int x, y;
    while(m--){
        cin>>x>>y;
        add(x, y);
        r[y]++;
    }
    bfs();
    return 0;
}

最短路

帮助理解
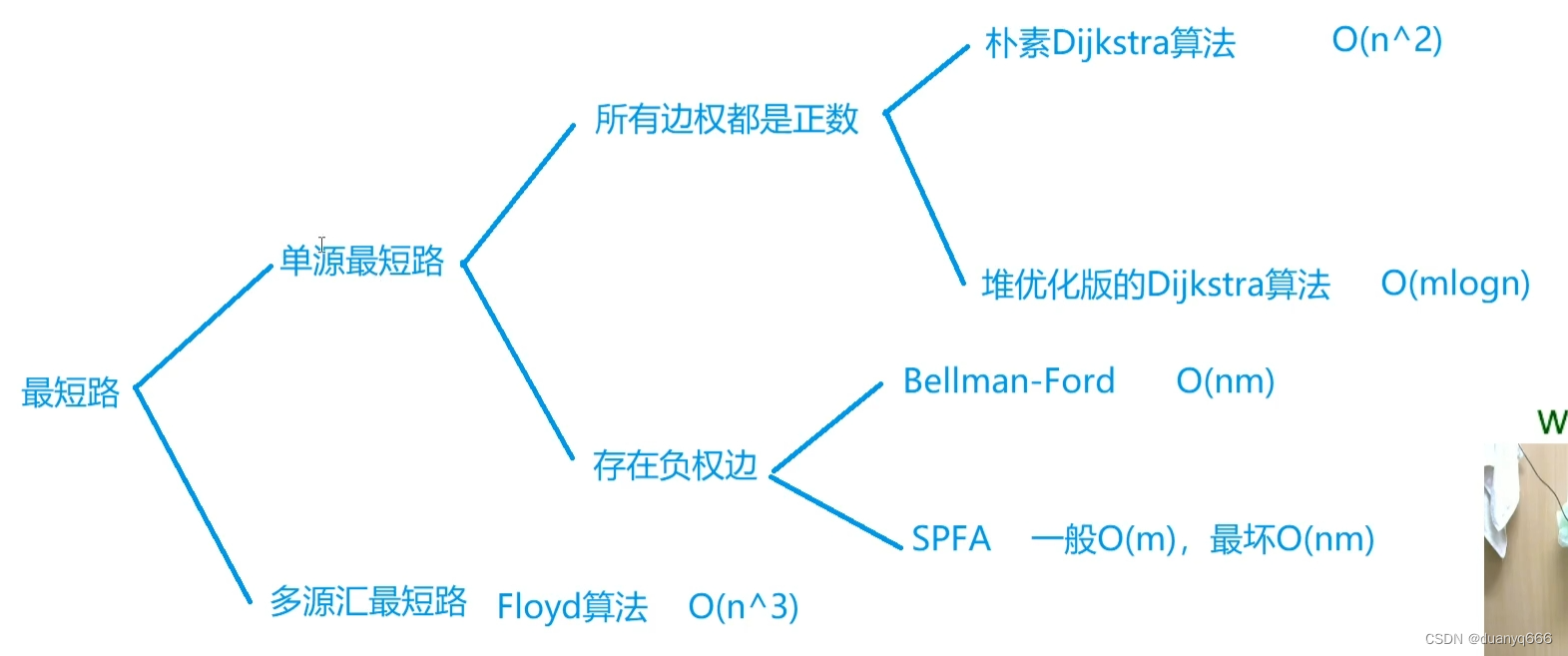
在这里插入图片描述

Dijkstra

Dijkstra求最短路 I

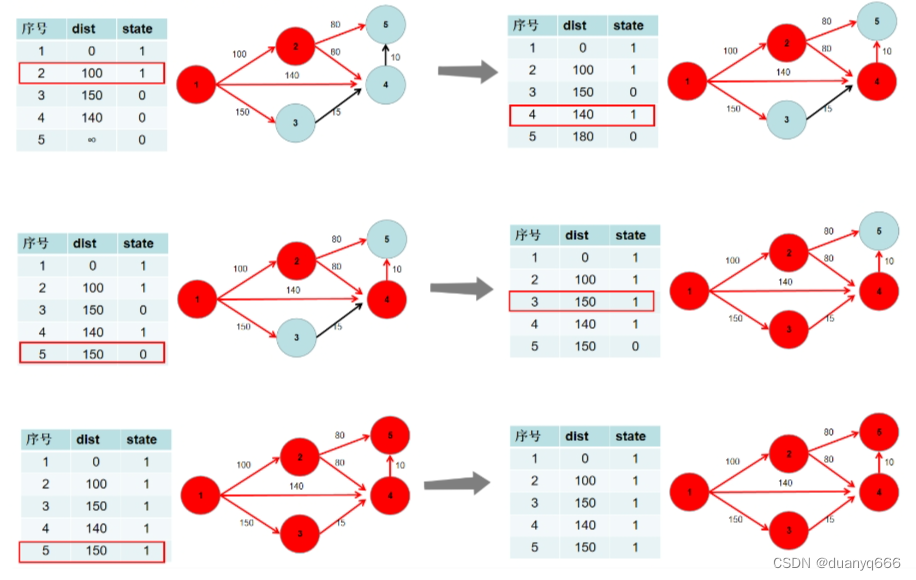
在这里插入图片描述

#include<iostream>
#include<cstring>
using namespace std;
const int N = 510;
int g[N][N], d[N], b[N];
int n, m;

void dijkstra(int u){
    memset(d, 0x3f, sizeof(d));
    d[u] = 0;
    for(int i = 0; i < n; i++){
        int t = -1;
        for(int j = 1; j <= n; j++)
            if(!b[j] && (t == -1 || d[t] > d[j])) t = j;
        b[t] = 1;
        for(int j = 1; j <= n; j++)
            d[j] = min(d[j], d[t] + g[t][j]);
    }
    cout<<((d[n] == 0x3f3f3f3f) ? -1 : d[n]);
}

int main(){
    memset(g, 0x3f, sizeof(g));
    cin>>n>>m;
    int x, y, z;
    while(m--){
        cin>>x>>y>>z;
        g[x][y] = min(g[x][y], z);
    }
    dijkstra(1);
    return 0;
}

Dijkstra求最短路 II

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 2e5;
int h[N], e[N], ne[N], w[N], idx; //w[i]存储上个点到i的距离
int d[N], b[N];
int n, m;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q; //小根堆，第一个元素存储距离，第二个元素存储下标

void add(int x, int y, int z){
    e[idx] = y;
    w[idx] = z;
    ne[idx] = h[x];
    h[x] = idx;
    idx++;
}

void dijkstra(int u){
    memset(d, 0x3f, sizeof(d));
    d[u] = 0;
    q.push(make_pair(0, 1));
    while(q.size()){
        auto t = q.top();
        q.pop();
        int x = t.first, y = t.second;
        if(b[y]) continue; //如果遍历过就退出
        b[y] = 1;
        for(int i = h[y]; i != -1; i = ne[i]){
            int j = e[i];
            if(d[j] > x + w[i]){
                d[j] = x + w[i];
                q.push(make_pair(d[j], j));
            }
        }
    }
    cout<<(d[n] == 0x3f3f3f3f ? -1 : d[n]);
}

int main(){
    memset(h, -1, sizeof(h));
    cin>>n>>m;
    int x, y, z;
    while(m--){
        cin>>x>>y>>z;
        add(x, y, z);
    }
    dijkstra(1);
    return 0;
}

增加点权，求有多少条最短路

题目链接

#include<iostream>
#include<cstring>
using namespace std;
int g[505][505], dis[505], st[505];
int a[505], paths[505], teams[505];
int n, m, c1, c2;

void dj(int u){
    teams[u] = a[u];
    paths[u] = 1;
    dis[u] = 0;
    for(int j = 0; j < n; j++){
        int t = -1;
        for(int i = 0; i < n; i++){
            if(!st[i] && (t == -1 || dis[t] > dis[i])){
                t = i;
            }
        }
        st[t] = 1;
        for(int i = 0; i < n; i++){
            if(dis[i] > dis[t] + g[t][i]){
                dis[i] = dis[t] + g[t][i]; 
                paths[i] = paths[t]; //继承路径条数
                teams[i] = teams[t] + a[i]; //更新救援队人数
            }else if(dis[i] == dis[t] + g[t][i]){
                if(teams[i] < teams[t] + a[i]){
                    teams[i] = teams[t] + a[i]; //选救援队人数更多的
                } 
                paths[i] += paths[t]; //累加路径条数
            }
        }
    }
}

int main(){
    memset(g, 0x3f, sizeof(g));
    cin>>n>>m>>c1>>c2;
    for(int i = 0; i < n; i++) cin>>a[i];
    while(m--){
        int x, y, z;
        cin>>x>>y>>z;
        g[x][y] = g[y][x] = min(g[x][y], z);
    }
    memset(dis, 0x3f, sizeof(dis));
    dj(c1);
    cout<<paths[c2]<<" "<<teams[c2];
    return 0;
}

增加边权，求花费最少

题目链接

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
int g[505][505], dis[505], st[505];
int cost[505][505], c[505], pre[505];
vector<int> path;
int n, m, s, d;

void dj(int u){
    dis[u] = 0;
    c[u] = 0;
    for(int i = 0; i < n; i++){
        int t = -1;
        for(int j = 0; j < n; j++){
            if(!st[j] && (t == -1 || dis[t] > dis[j])){
                t = j;
            }
        }
        st[t] = 1;
        for(int j = 0; j < n; j++){
            if(dis[j] > dis[t] + g[t][j]){
            	pre[j] = t;
                dis[j] = dis[t] + g[t][j];
                c[j] = c[t] + cost[t][j];
            }else if(dis[j] == dis[t] + g[t][j] && c[j] > c[t] + cost[t][j]){
            	pre[j] = t;
                c[j] = c[t] + cost[t][j];
            }
        }
    }
}

int main(){
    memset(g, 0x3f, sizeof(g));
    memset(dis, 0x3f, sizeof(dis));
    memset(c, 0x3f, sizeof(c));
    memset(cost, 0x3f, sizeof(cost));
    cin>>n>>m>>s>>d;
    while(m--){
        int x, y, z, h;
        cin>>x>>y>>z>>h;
        g[x][y] = g[y][x] = min(g[x][y], z);
        cost[x][y] = cost[y][x] = min(cost[x][y], h);
    }
    for(int i = 0; i < n; i++) pre[i] = i;
    dj(s);
    int q = d;
    while(q != s){
    	path.push_back(q);
    	q = pre[q];
	}
	path.push_back(s);
	int p = path.size();
	for(int i = p - 1; i >= 0; i--) cout<<path[i]<<" ";
	cout<<dis[d]<<" "<<c[d];
    return 0;
}

bellman-ford

有边数限制的最短路

如果负环在1到n的路径上，那就不存在最短路

#include<iostream>
#include<cstring>
using namespace std;
const int N = 510, M = 1e4 + 10;
int d[N], b[N]; //b数组备份
int n, m, k;
struct E{
    int x, y, z;
}e[M];

void bellman_ford(int u){
    memset(d, 0x3f, sizeof(d));
    d[u] = 0;
    //最多k条边
    for(int i = 0; i < k; i++){
        //每次只更新一条串联路径，防止更新了多条串联路径
        memcpy(b, d, sizeof(d));
        for(int j = 0; j < m; j++){
            int x = e[j].x, y = e[j].y, z = e[j].z;
            d[y] = min(d[y], b[x] + z);
        }
    }
    if(d[n] > 0x3f3f3f3f / 2) cout<<"impossible";
    else cout<<d[n];
}

int main(){
    cin>>n>>m>>k;
    int x, y, z;
    for(int i = 0; i < m; i++){
        cin>>x>>y>>z;
        e[i] = {x, y, z};
    }
    bellman_ford(1);
    return 0;
}

spfa

spfa求最短路

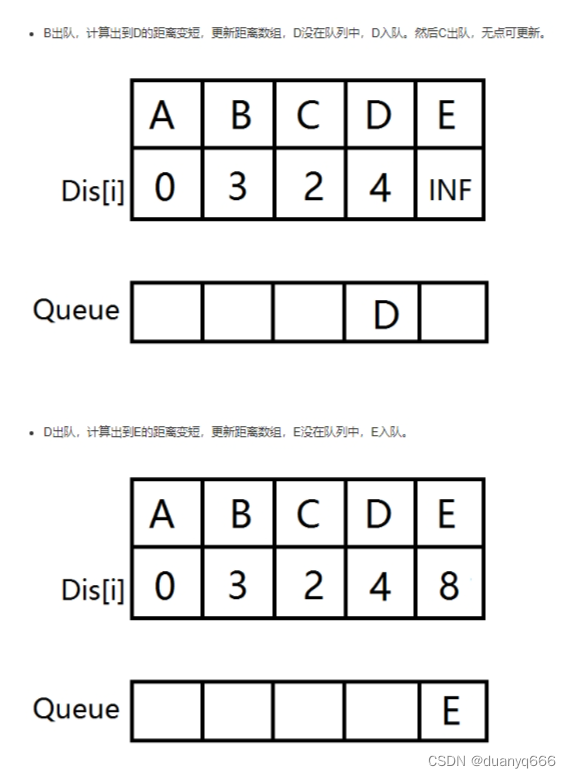
在这里插入图片描述
在这里插入图片描述

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], w[N], idx;
int dis[N], st[N];
int q[N], hh, tt = -1;
int n, m;

void add(int x, int y, int z){
    e[idx] = y;
    w[idx] = z;
    ne[idx] = h[x];
    h[x] = idx;
    idx++;
}

void spfa(int u){
    memset(dis, 0x3f, sizeof(dis));
    dis[u] = 0;
    q[++tt] = u;
    st[u] = 1;
    while(hh <= tt){
        int t = q[hh++];
        //有环，所以可能一个点会遍历两次
        st[t] = 0;
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            if(dis[j] > dis[t] + w[i]){
                dis[j] = dis[t] + w[i];
                if(!st[j]){
                    q[++tt] = j;
                    st[j] = 1;
                }
            }
        }
    }
    if(dis[n] == 0x3f3f3f3f) cout<<"impossible";
    else cout<<dis[n];
}

int main(){
    memset(h, -1, sizeof(h));
    cin>>n>>m;
    int x, y, z;
    for(int i = 0; i < m; i++){
        cin>>x>>y>>z;
        add(x, y, z);
    }
    spfa(1);
    return 0;
}

spfa判断负环

#include<iostream>
#include<cstring>
using namespace std;
const int N = 2e3 + 10, M = 1e4 + 10;;
int h[N], e[M], ne[M], w[M], idx;
int dis[N], st[N], cnt[N];
int q[N * N], hh, tt = -1; //有环的时候，一个元素可能会一直插入队列，所以要开N * N
int n, m;

void add(int x, int y, int z){
    e[idx] = y;
    w[idx] = z;
    ne[idx] = h[x];
    h[x] = idx;
    idx++;
}

void spfa(){
    //存在的负权回路，不一定从1开始
    for(int i = 1; i <= n; i++){
        q[++tt] = i;
        st[i] = 1;
    }
    while(hh <= tt){
        int t = q[hh++];
        //有环，所以可能一个点会遍历两次
        st[t] = 0;
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            if(dis[j] > dis[t] + w[i]){
                dis[j] = dis[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if(cnt[j] >= n){
                    cout<<"Yes";
                    return;
                }
                if(!st[j]){
                    q[++tt] = j;
                    st[j] = 1;
                }
            }
        }
    }
    cout<<"No";
}

int main(){
    memset(h, -1, sizeof(h));
    cin>>n>>m;
    int x, y, z;
    for(int i = 0; i < m; i++){
        cin>>x>>y>>z;
        add(x, y, z);
    }
    spfa();
    return 0;
}

Floyd

Floyd求最短路

f(k, i, j) = f(k - 1, i, k) + f(k - 1, k, j);

#include<iostream>
using namespace std;
const int N = 210;
int f[N][N];
int n, m, k;

void floyd(){
    for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
}

int main(){
    cin>>n>>m>>k;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            if(i == j) f[i][j] = 0;
            else f[i][j] = 0x3f3f3f3f;
    int x, y, z;
    for(int i = 1; i <= m; i++){
        cin>>x>>y>>z;
        f[x][y] = min(f[x][y], z);
    }
    floyd();
    for(int i = 1; i <= k; i++){
        cin>>x>>y;
        //可能存在负权边
        if(f[x][y] > 0x3f3f3f3f / 2) cout<<"impossible"<<endl;
        else cout<<f[x][y]<<endl;
    }
    return 0;
}

最小生成树

在这里插入图片描述

Prim

Kruskal

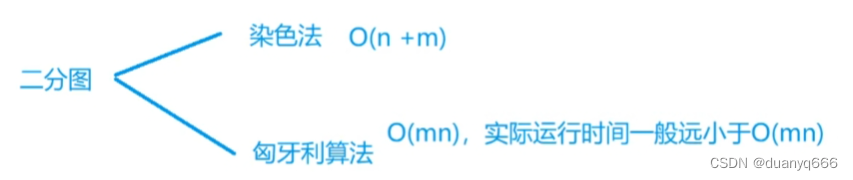
二分图

在这里插入图片描述

染色法判定二分图

匈牙利算法

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1443040.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ubuntu篇---ubuntu安装python3.9

ubuntu篇---ubuntu安装python3.9

ubuntu篇—ubuntu安装python3.9 在ubuntu上安装Python有两种方法:在线安装和源码编译安装。 方法1&#xff1a;使用apt在线安装 1.更新软件包列表并安装必备组件&#xff1a; $ sudo apt update $ sudo apt install software-properties-common2.将Deadsnakes PPA添加到系统…
阅读更多...
LLM之LangChain（七）| 使用LangChain，LangSmith实现Prompt工程ToT

LLM之LangChain（七）| 使用LangChain，LangSmith实现Prompt工程ToT

如下图所示&#xff0c;LLM仍然是自治代理的backbone&#xff0c;可以通过给LLM增加以下模块来增强LLM功能: Prompter AgentChecker ModuleMemory moduleToT controller 当解决具体问题时&#xff0c;这些模块与LLM进行多轮对话。这是基于LLM的自治代理的典型情况&#xff0c;…
阅读更多...
AutoSAR（基础入门篇）7.1-汽车电子开发软件DaVinci Developer界面简介

AutoSAR（基础入门篇）7.1-汽车电子开发软件DaVinci Developer界面简介

目录 一、Dev界面简介 二、Dev使用流程简介 一、Dev界面简介 经典的是更老的版本，博主这里用的是较新一点的版本，不过大家不必担心版本问题，因为操作几乎都一样。我们先简单浏览一遍这个界面，大致从 上往下看可以分为这么几部分： 1. 导航栏：File那一排 2. 工具栏&…
阅读更多...
门诊单据打印用什么软件，线下处方单生成系统教程

门诊单据打印用什么软件，线下处方单生成系统教程

门诊单据打印用什么软件&#xff0c;线下处方单生成系统教程 一、前言 以下软件教程以 佳易王诊所电子处方管理系统软件V17.3为例说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 如上图&#xff0c;电子处方或病历记录开单生成保存后&#xff0c;可…
阅读更多...
每日五道java面试题之java基础篇（三）

每日五道java面试题之java基础篇（三）

第一题. switch 是否能作⽤在 byte/long/String 上&#xff1f; Java5 以前 switch(expr)中&#xff0c;expr 只能是 byte、short、char、int。从 Java 5 开始&#xff0c;Java 中引⼊了枚举类型&#xff0c; expr 也可以是 enum 类型。从 Java 7 开始&#xff0c;expr 还可以…
阅读更多...
序列流和反序列流

序列流和反序列流

先看看它们在io体系中的位置&#xff1a;--------------------------------------------------------------------------------- 序列化流&#xff1a; 可以将java中的对象写到本地文件中&#xff0c;如这样的数据写到文件后变成这样----->目的就是防止别人看得懂&#xff…
阅读更多...
解决“使用Edge浏览器每次鼠标点击会出现一个黑色边框”的问题

解决“使用Edge浏览器每次鼠标点击会出现一个黑色边框”的问题

目录 一 问题描述 二 解决方案 三 方案来源 四 参考资料 & AI工具 一 问题描述 为了方便进行收藏夹同步&#xff0c;开始从Chrome浏览器切换到Edge浏览器。在使用Edge浏览器过程中发现“每次鼠标点击会出现一个黑色边框”&#xff08;效果如下图所示&#xff09;&#…
阅读更多...
tkinter-TinUI-xml实战（10）展示画廊

tkinter-TinUI-xml实战（10）展示画廊

tkinter-TinUI-xml实战&#xff08;10&#xff09;展示画廊 引言声明文件结构核心代码主界面统一展示控件控件展示界面单一展示已有展示多类展示 最终效果在这里插入图片描述 ![](https://img-blog.csdnimg.cn/direct/286fcaa2fa5648a992a0ac79b4efad82.png) ………… 结语 引言…
阅读更多...
【Larry】英语学习笔记语法篇——换一种方式理解词性

【Larry】英语学习笔记语法篇——换一种方式理解词性

目录 一、换一种方式理解词性 1、名词、形容词、副词&#xff0c;这就是一切 2、词性之间的修饰关系 3、介词其实很简单 形容词属性的介词短语 副词属性的介词短语 ①修饰动词 ②修饰形容词 ③修饰其他副词 一、换一种方式理解词性 1、名词、形容词、副词&#xff0c…
阅读更多...
服务器内存使用率多少会影响正常访问？

服务器内存使用率多少会影响正常访问？

在探讨服务器内存使用率多少会影响正常访问这个问题时&#xff0c;我们首先要明白&#xff0c;服务器的性能和稳定性与内存使用状况息息相关。当服务器的内存使用率过高时&#xff0c;可能会导致系统运行缓慢、程序崩溃或者出现其他一些异常情况&#xff0c;从而影响到正常的网…
阅读更多...
Mysql-数据库优化-客户端连接参数

Mysql-数据库优化-客户端连接参数

客户端参数 原文地址 # 连接池配置 # 初始化连接数 spring.datasource.druid.initial-size1 # 最小空闲连接数&#xff0c;一般设置和initial-size一致 spring.datasource.druid.min-idle1 # 最大活动连接数&#xff0c;一个数据库能够支撑最大的连接数是多少呢&#xff1f; …
阅读更多...
【开源】JAVA+Vue.js实现衣物搭配系统

【开源】JAVA+Vue.js实现衣物搭配系统

目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 衣物档案模块2.2 衣物搭配模块2.3 衣物收藏模块 三、系统设计3.1 用例设计3.2 E-R图设计3.3 数据库设计3.3.1 衣物档案表3.3.2 衣物搭配表3.3.3 衣物收藏表 四、系统实现4.1 登录页4.2 衣物档案模块4.3 衣物搭配模块4.4…
阅读更多...
干掉Xshell，这款开源的终端工具逼格真高！

干掉Xshell，这款开源的终端工具逼格真高！

GitHub 上已经有 53.7k 的 star 了&#xff0c;这说明 Tabby 非常的受欢迎&#xff1a; https://github.com/eugeny/tabby Tabby 是一个高度可定制化的 跨平台的终端工具&#xff0c;支持 Windows、macOS 和 Linux&#xff0c;自带 SFTP 功能&#xff0c;能与 Linux 服务器轻…
阅读更多...
《CSS 简易速速上手小册》第4章：视觉美学（2024 最新版）

《CSS 简易速速上手小册》第4章：视觉美学（2024 最新版）

文章目录 4.1 颜色理论在 CSS 设计中的应用&#xff1a;网页的调色盘4.1.1 基础知识4.1.2 重点案例&#xff1a;创建一个具有情感设计的登录页面4.1.3 拓展案例 1&#xff1a;使用颜色增强信息的可视化表示4.1.4 拓展案例 2&#xff1a;利用颜色创建网站的品牌身份 4.2 字体与文…
阅读更多...
VMWare虚拟机安装

VMWare虚拟机安装

VMWare虚拟机安装 0.Linux运行平台介绍1. VMWare 虚拟软件安装检查虚拟网卡是否安装 创建VMWare虚拟机对创建虚拟机的内容进行设置挂在要安装的CentOS的ISO文件 0.Linux运行平台介绍 Linux的运行平台一共有两种,其中包括物理机平台和虚拟机平台,在学习阶段当中建议使用虚拟机 …
阅读更多...
用的到的linux-查找find-Day4

用的到的linux-查找find-Day4

前言&#xff1a; 在上一节&#xff0c;我们了解到rm删除命令&#xff0c;一共拥有三种模式&#xff0c;即-i默认只能删除文件且会提示确认&#xff0c;其次是-r 遍历删除&#xff0c;用于删除目录及目录下的文件&#xff0c;同样需确认后才会删除&#xff0c;最后为-f为强制删…
阅读更多...
高级FPGA开发之基础协议PCIe(二)

高级FPGA开发之基础协议PCIe(二)

高级FPGA开发之基础协议之PCIe&#xff08;二&#xff09; 一、TLP报文类型 在PCIe总线中&#xff0c;存储器读写、I/O读写和配置读写请求TLP主要由以下几类报文组成&#xff1a; 1.1 存储器读请求TLP和读完成TLP 当PCIe主设备&#xff08;RC或者EP&#xff09;访问目标设备…
阅读更多...
【前端高频面试题--TypeScript篇】

【前端高频面试题--TypeScript篇】

&#x1f680; 作者 &#xff1a;“码上有前” &#x1f680; 文章简介 &#xff1a;前端高频面试题 &#x1f680; 欢迎小伙伴们 点赞&#x1f44d;、收藏⭐、留言&#x1f4ac; 高频前端面试题--Vue3.0篇 什么是TypeScript&#xff1f;TypeScript数据类型TypeScript中命名空…
阅读更多...
「daily updating」k3s + openfaas serverless bench 踩坑指南持续更新中

「daily updating」k3s + openfaas serverless bench 踩坑指南持续更新中

OpenFaas从入门到实战 – 踩坑指南 &#xff5c; k3dOpenFaas | deploy your first python function https://blog.alexellis.io/first-faas-python-function/ https://docs.openfaas.com/deployment/kubernetes/ 搭建环境&#xff1a;第一种方法失败&#xff0c;第二种方法…
阅读更多...
CSP-202112-2-序列查询新解

CSP-202112-2-序列查询新解

CSP-202112-2-序列查询新解 【70分思路】 【暴力枚举】按照题目思路遍历一遍f(x)和g(x)&#xff0c;计算error(A)&#xff0c;时间复杂度为O(N)&#xff0c;时间超限。 #include <iostream> using namespace std; int main() {long long n, N, sum 0;cin >> n …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023