1、MT1217矩阵乘法

输入3X4整型矩阵A和4X3的整型矩阵B，计算A*B，放到矩阵C里面，输出矩阵C。

格式

输入格式：

分两行输入两个矩阵，空格分隔。

输出格式：

按矩阵形式输出，整型，每个数字占3列，空格分隔。

样例 1

输入：

3 0 0 7 0 0 0 -1 0 2 0 0    
4 1 0 0 1 -1 0 2 1 0 2 1 

输出：

 12  17   7
  0  -2  -1
  0   2  -2

分析过程

本题的要点在于矩阵乘法如何计算，这就考验线性代数学的咋样了。

对于3X4整型矩阵A和4X3的整型矩阵B的乘积，以样例1为例，说明计算过程：

        3X4整型矩阵A：

3 0 0 7

0 0 0 -1

0 2 0 0

        4X3的整型矩阵B：

4 1 0

0 1 -1

0 2 1

0 2 1

这两个矩阵相乘，最终得到的结果是3*3的矩阵，计算过程如下：

首先结果矩阵C的第一个值为矩阵A的第一行乘以矩阵B的第二行，依次相乘然后相加。

 *    

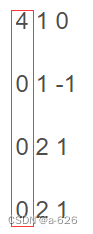
在此样例中，就是3*4+0*0+0*0+7*0=12，即矩阵C的第一个元素为12。

矩阵C的第一行第二个值为矩阵A的第一行乘以矩阵B的第二列，

  *    

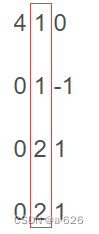
即3*1+0*1+0*2+7*2=17，依次向下即可。

按照这个解决思路，写下代码：

实现代码

#include<bits/stdc++.h> 

using namespace std;

int main( )
{
    int A[3][4]={0},B[4][3]={0},C[3][3]={0};
    for(int i=0;i<3;i++){
        for(int j=0;j<4;j++){
            cin >> A[i][j];
        }
    }
    for(int i=0;i<4;i++){
        for(int j=0;j<3;j++) 
        cin >> B[i][j];
    }
/*这里就是矩阵的乘法的代码，这里用到了三重循环，因为矩阵C是３＊３矩阵，而A是３＊４矩阵，B是４＊３矩阵，所以循环条件有三个，３，３，４，按照这个写下如下代码*/
    for(int i=0;i<3;i++){
        for(int j=0;j<3;j++){
            for(int z=0;z<4;z++){
                C[i][j]+=A[i][z]*B[z][j];
            }
        }
    } 
    for(int i=0;i<3;i++){
        for(int j=0;j<3;j++) 
            printf("%3d ",C[i][j]) ;
        cout << "\n";
    }
    
    return 0;
}

下面这个是参考别人的代码， 这个代码没有将相乘得到的值存入矩阵C中，而是直接输出，所以，在输出的时候需要设置一个计数器，当计数到３的倍数的时候，换行。其余的与上面的思想是一样的。

#include<bits/stdc++.h> 

using namespace std;

int main( )
{
    int A[100][100],B[100][100],cnt,ans;
    for(int i=1;i<=3;i++){
        for(int j=1;j<=4;j++){
            cin >> A[i][j];
        }
    }
    for(int i=1;i<=4;i++){
        for(int j=1;j<=3;j++) 
            cin >> B[i][j];
    }
    cnt=1;
    for(int i=1;i<=3;i++){
        for(int k=1;k<=3;k++){
            ans=0;
            for(int j=1;j<=4;j++) ans+=A[i][j] * B[j][k];
            printf("%3d ",ans);
            if(cnt%3==0) printf("\n");
            cnt++;
        }
    }
    return 0;
}

２、MT1219斐波那契数列II

判断数字N（N<2929）是否为斐波那契数列中出现的数，输出YES或者NO。

格式

输入格式：

输入整型

输出格式：

输出YES或者NO

样例 1

输入：

5

输出：

YES

相关知识点

斐波那契数列指的是这样的一个数列：1、1、2、3、5、8、13、21、34、……，这个数列从第 3 项开始，每一项都等于前面两项之和。

实现代码

#include<bits/stdc++.h> 

using namespace std;

int judge(int n){//此函数用于计算斐波那契数列的值
    int f1 = 1;
    int f2 = 1;
    int fn;
    if(n==0){
        return 0;
    }else{
        for(int i=1;i<=n;i++){
            fn=f1+f2;
            f1=f2;
            f2=fn;
        }
        return f1;
    }
}
int main( )
{
    int n;
    cin >> n;
    for(int i=1;i<=n;i++){
        if(n==judge(i)){
            cout << "YES";
            return 0;
        }
    }
    cout << "NO";
    return 0;
}

 

明天继续吧。