目录

---

一、前言

二、正文

Ⅰ.基于过采样算法

Ⅱ.基于欠采样算法

Ⅲ..基于过采样和欠采样的综合算法

三、结语

---

一、前言

大多数情况下，使用的数据集是不完美的，会出现各种各样的问题，尤其针对分类问题的时候，会出现类别不平衡的问题。例如：在垃圾邮件分类时，垃圾邮件数据会有较少的样本量，从而导致两种类型的邮件数据量差别很大；在欺诈监测数据集中，往往包含的欺诈样本并没有那么多。处理这类数据集的分类的时候，需要对数据集的类不平衡问题进行处理。 

二、正文

  

Ⅰ.基于过采样算法

from imblearn.datasets import make_imbalance
from imblearn.over_sampling import KMeansSMOTE,SMOTE,SVMSMOTE
from imblearn.under_sampling import AllKNN,CondensedNearestNeighbour,NearMiss
from imblearn.combine import SMOTEENN,SMOTETomek
im_x,im_y=make_imbalance(pca_wine_x,wine_y,sampling_strategy={0:30,1:70,2:20},randim_state=12)
print(np.unique(im_y,return_counts=True))
#输出结果
(array([0, 1, 2]), array([30, 70, 20], dtype=int64))

首先准备不配合的数据将其读取，这些都是前面用过的。imblearn则是专门处理数据不平衡问题的库。

kmeans=KMeansSMOTE(random_state=123,k_neighbors=3)
kmeans_x,kmeans_y=kmeans.fit_resample(im_x,im_y)
print("KMeansSMOTE：",np.unique(kmeans_y,return_counts=True))
smote=SMOTE(random_state=123,k_neighbors=3)
smote_x,smote_y=smote.fit_resample(im_x,im_y)
print("SMOTE：",np.unique(smote_y,return_counts=True))
svm=SVMSMOTE(random_state=123,k_neighbors=3)
svm_x,svm_y=svm.fit_resample(im_x,im_y)
print("SvmSMOTE：",np.unique(svm_y,return_counts=True))

SVMSMOTE
#输出结果
KMeansSMOTE： (array([0, 1, 2]), array([71, 70, 70], dtype=int64))
   SMOTE：    (array([0, 1, 2]), array([70, 70, 70], dtype=int64))
  SvmSMOTE：  (array([0, 1, 2]), array([70, 70, 53], dtype=int64))

针对数据平衡方法---过采样，可使用以上方法。

接下来我们通过可视化，把类别数据量展现：

colors=['red','blue','green']
shape=['o','s','*']
fig=plt.figure(figsize=(10,6))
plt.subplot(2,2,1)
plt.title('Ori')
for ii,y in enumerate(im_y):
      plt.scatter(im_x[ii,0],im_x[ii,1],s=40,c=colors[y],marker=shape[y])

plt.subplot(2,2,2)
plt.title('Kmeans')
for ii,y in enumerate(kmeans_y):
      plt.scatter(kmeans_x[ii,0],kmeans_x[ii,1],s=40,c=colors[y],marker=shape[y])

plt.subplot(2,2,3)
plt.title('smote')
for ii,y in enumerate(smote_y):
      plt.scatter(smote_x[ii,0],smote_x[ii,1],s=40,c=colors[y],marker=shape[y])

plt.subplot(2,2,4)
plt.title('svms')
for ii,y in enumerate(svm_y):
      plt.scatter(svm_x[ii,0],svm_x[ii,1],s=40,c=colors[y],marker=shape[y])

plt.show()

 让三种数据的类别比例接近 1:1:1，用四个图来对比更加直观。

 

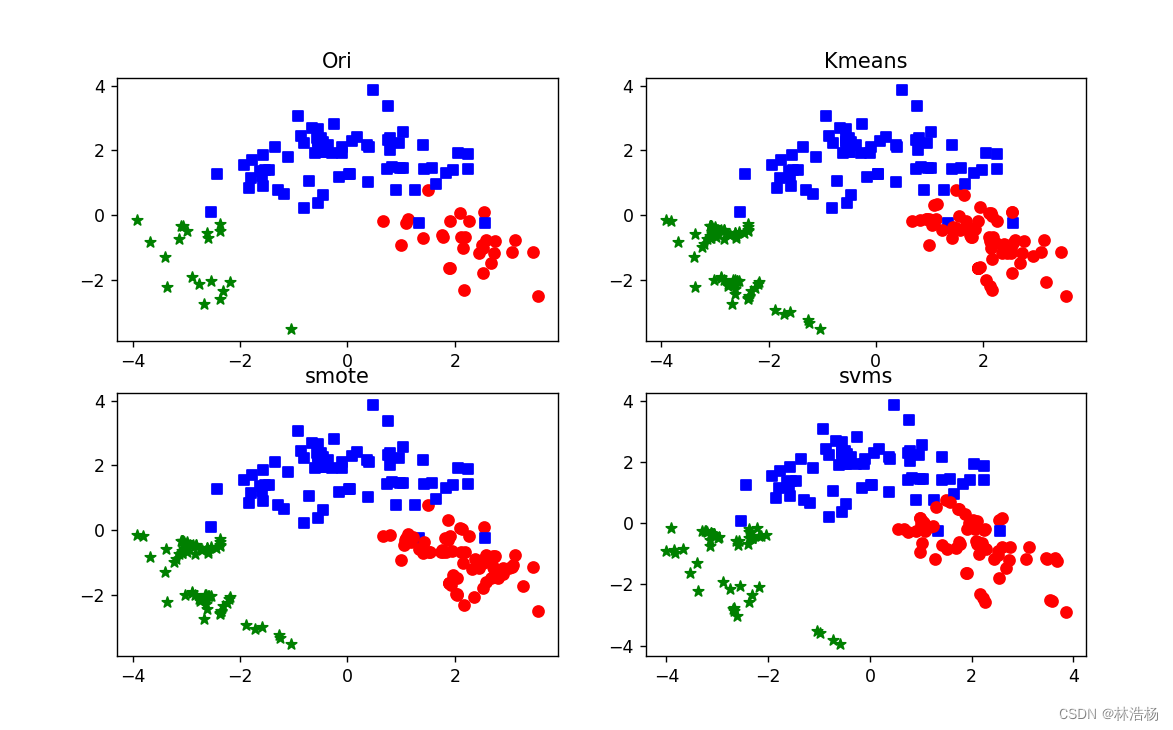
不同算法生成的位置是有所差异的，在少样本的数据类周围生成新的样本数量。 

Ⅱ.基于欠采样算法

cnn=CondensedNearestNeighbour(random_state=123,n_neighbors=7,n_seeds_S=20)
cnn_x,cnn_y=cnn.fit_resample(im_x,im_y)
print("CondensedNearestNeighbour:",np.unique(cnn_y,return_counts=True))

allknn=AllKNN(n_neighbors=10)
allknn_x,allknn_y=allknn.fit_resample(im_x,im_y)
print("AllKNN:",np.unique(allknn_y,return_counts=True))


nmiss=NearMiss(n_neighbors=3)
nmiss_x,nmiss_y=nmiss.fit_resample(im_x,im_y)
print("NearMiss:",np.unique(nmiss_y,return_counts=True))

#输出结果
CondensedNearestNeighbour: (array([0, 1, 2]), array([20, 22, 20], dtype=int64))
AllKNN: (array([0, 1, 2]), array([22, 56, 20], dtype=int64))
NearMiss: (array([0, 1, 2]), array([20, 20, 20], dtype=int64))

针对数据平衡的方法一一欠采样，如上介绍的方法都是使用特定的方法减少样本数量较多类别的样本量，从而使三种数据的样本接近1:1:1。通过可视化有如下效果：

from imblearn.under_sampling import AllKNN,CondensedNearestNeighbour,NearMiss
colors=['red','blue','green']
shape=['o','s','*']
fig=plt.figure(figsize=(14,10))
plt.subplot(2,2,1)
plt.title('Ori')
for ii,y in enumerate(im_y):
      plt.scatter(im_x[ii,0],im_x[ii,1],s=40,c=colors[y],marker=shape[y])

plt.subplot(2,2,2)
plt.title('CondensedNearestNeighbour')
for ii,y in enumerate(cnn_y):
      plt.scatter(cnn_x[ii,0],cnn_x[ii,1],s=40,c=colors[y],marker=shape[y])

plt.subplot(2,2,3)
plt.title('AllKNN')
for ii,y in enumerate(allknn_y):
      plt.scatter(allknn_x[ii,0],allknn_x[ii,1],s=40,c=colors[y],marker=shape[y])

plt.subplot(2,2,4)
plt.title('svms')
for ii,y in enumerate(nmiss_y):
      plt.scatter(nmiss_x[ii,0],nmiss_x[ii,1],s=40,c=colors[y],marker=shape[y])

plt.show()

没有什么特别的变化，只是改变了要展现的变量名，然后通过迭代散点绘制而成。 

从中可以看出三种欠采样算法都是减少样本量较多的数据样本，但是不同的算法减去的样本位置和数量有所差异。 

Ⅲ..基于过采样和欠采样的综合算法

from imblearn.combine import SMOTEENN,SMOTETomek
smoteenn=SMOTEENN(random_state=123)
smoteenn_x,smoteenn_y=smoteenn.fit_resample(im_x,im_y)
print("SMOTEENN:",np.unique(smoteenn_y,return_counts=True))
#输出结果
SMOTEENN： (array([0, 1, 2]), array([67, 64, 69], dtype=int64))

smoteet=SMOTETomek(random_state=123)
smoteet_x,smoteet_y=smoteet.fit_resample(im_x,im_y)
print("SMOTETomek：",np.unique(smoteet_y,return_counts=True))
#输出结果
SMOTETomek： (array([0, 1, 2]), array([69, 69, 70], dtype=int64))

根据上面三种也是能够看出类别比例接近1:1:1,但是只有后者的方法更加接近这个规律，那我们通过可视化观察一番：

colors=['red','blue','green']
shape=['o','s','*']
fig=plt.figure(figsize=(14,10))
plt.subplot(1,2,1)
plt.title('Smoteenn')
for ii,y in enumerate(smoteenn_y):
      plt.scatter(smoteenn_x[ii,0],smoteenn_x[ii,1],s=40,c=colors[y],marker=shape[y])

plt.subplot(1,2,2)
plt.title('Smoteet')
for ii,y in enumerate(smoteet_y):
      plt.scatter(smoteet_x[ii,0],smoteet_x[ii,1],s=40,c=colors[y],marker=shape[y])


plt.show()

 方法也是没有多大的改变，照葫芦画瓢。

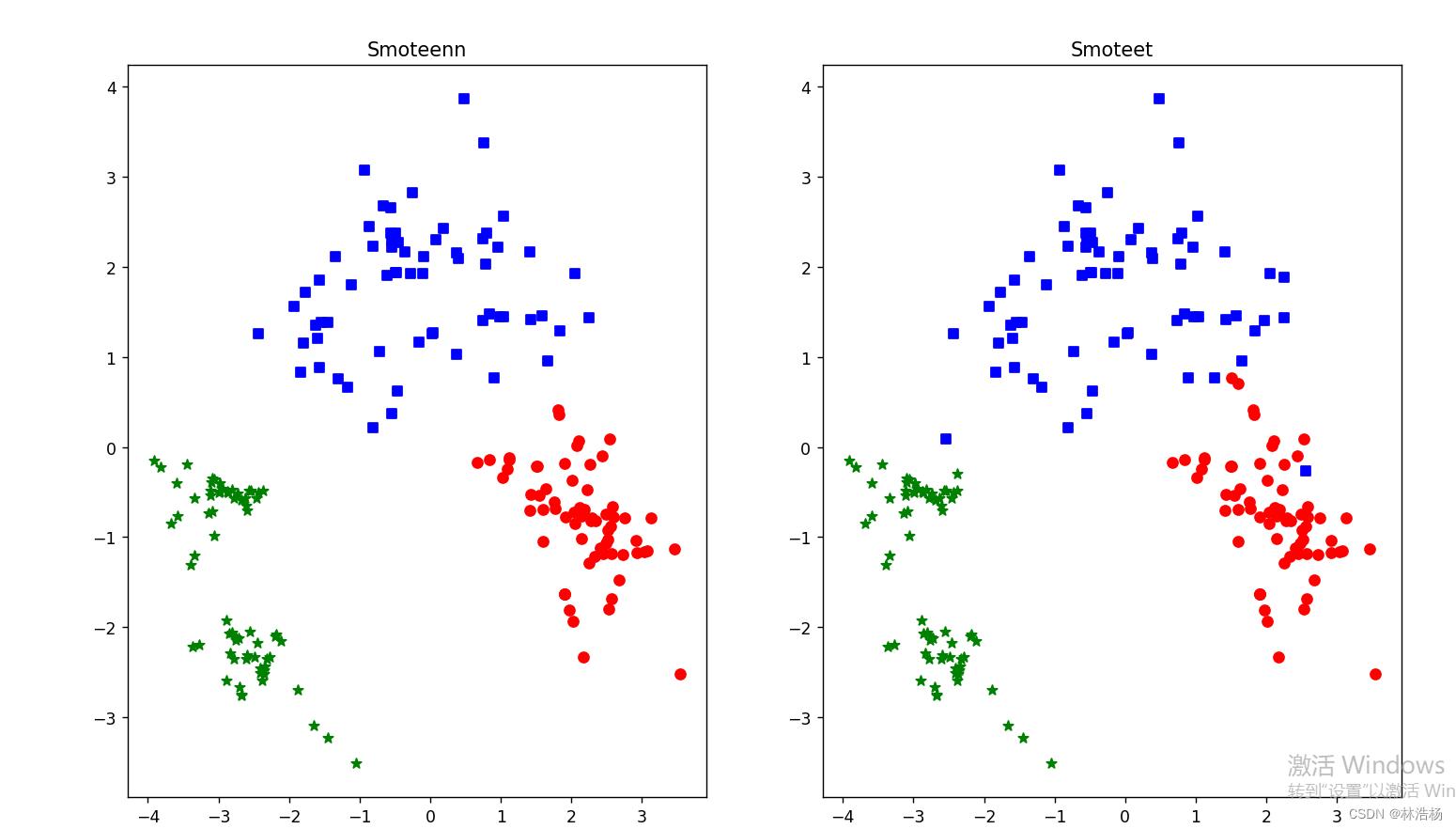
与其他采样的结果一样，可以看到样本位置上的差异。

三、结语

数据分析的整个过程的介绍就结束了，那接下来就是关于模型的选择与评估问题，只不过对数据分析着实重要，在之后的几篇当中，我们需要对数据分析有着更加细致的了解或者案例切入。