paper链接：https://ieeexplore.ieee.org/abstract/document/7090642/

import math
import numpy as np
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置中文字体为黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号'-'显示为方块的问题

class CPG(object):
    def __init__(self, gait=0):

        self.gait_num = 3
        self.gait_names = ["Walk","Trot", "Pace", "Bound"]
        self.labels = ['FL', 'FR', 'HL', 'HR']

        # CPG构建基本参数
        self._alpha = 100
        self.leg_num = 4
        self.gait = gait
        self.mu_ = -1
        self._a = 50
        self.u1 = 0
        self.u2 = 0

        # 负载系数对相关参数影响
        self.BEAT_ = [0.75, 0.5, 0.5, 0.5]
        self.period_ = [0.6, 0.5, 0.5, 0.4]
        self._beta = self.BEAT_[0]
        self._t = self.period_[0]

        # 时间
        self.t_step = 0.001

        self.point_x = np.zeros(self.leg_num)
        self.point_y = np.zeros(self.leg_num)

        self.PHASE = [
            [0 * 2 * np.pi, 0.5 * 2 * np.pi, 0.25 * 2 * np.pi, 0.75 * 2 * np.pi],
            [0 * 2 * np.pi, 0.5 * 2 * np.pi, 0.5 * 2 * np.pi, 0 * 2 * np.pi],
            [0 * 2 * np.pi, 0.5 * 2 * np.pi, 0 * 2 * np.pi, 0.5 * 2 * np.pi],
            [0 * 2 * np.pi, 0 * 2 * np.pi, 0.5 * 2 * np.pi, 0.5 * 2 * np.pi],
        ]
        
        # 相对相位矩阵
        self.R_cell = np.zeros(shape=(self.leg_num, self.leg_num, 2, 2))

        self.Phi = None

        # 初始值，非0即可
        self.leg_x = None
        self.leg_y = None

        self.reset()
        
        # 计数，什么时候完成相位同步
        self.count_ = 0
        # 计数，什么时候结束步态转换
        self.t_count_ = 0

        self.init_phase()

    def init_phase(self):
        for _ in range(700):
            self.step()
    
    def reset(self):
        self._beta = self.BEAT_[self.gait]
        self._t = self.period_[self.gait]
        self.Phi = self.PHASE[self.gait]

        self.leg_x = np.ones(self.leg_num) * 0.0001
        self.leg_y = np.ones(self.leg_num) * 0.0001

        self.update_rotation_matrix()

    def next_gait(self):
        self.gait = (self.gait + 1) % self.gait_num
        self.reset()
        
    def update_rotation_matrix(self):        
        for i in np.arange(0, self.leg_num):
            for j in np.arange(0, self.leg_num):
                self.R_cell[j, i] = np.array([
                    [np.cos(self.Phi[i] - self.Phi[j]), - np.sin(self.Phi[i] - self.Phi[j])],
                    [np.sin(self.Phi[i] - self.Phi[j]), np.cos(self.Phi[i] - self.Phi[j])]
                ])
    
    def transit_gait(self, tau=0):
        self.t_count_ = self.t_count_ + 1
        # 步态在一个周期内完成转换
        if tau == 0:
            # walk to trot
            # beta/φ2从0.75变换到0.5
            # walk步态周期为0.6，假设在1s内完成转换，共200步，每步变换1/800=0.00125
            transit_step = 0.00125
            self.Phi[0] = 0
            # self.Phi[1] = 0.5
            phi2_ = 0.75 - transit_step * self.t_count_
            self.Phi[2] = phi2_ * 2 * np.pi
            self.Phi[3] = (phi2_ - 0.5) * 2 * np.pi
            # 更新占空比参数和周期参数
            self._beta = phi2_            
        else:
            # trot to gallop
            # φ1从0.5到0，0.5/200=1/400=0.0025
            transit_step = 0.0025
            phi1_ = 0.5 - transit_step * self.t_count_
            self.Phi[1] = phi1_ * 2 * np.pi
            self.Phi[3] = (0.5 - phi1_) * 2 * np.pi
        
        if self.t_count_ >= 200:
            self.t_count_ = 0
            if tau == 0:
                self._t = 0.5
            else:
                self._t = 0.4


        self.update_rotation_matrix()
    

    def step(self):
        if self.count_ > 400:
            self.mu_ = 1
            
        self.count_  = self.count_ + 1

        if self.count_ > 1200 and self.count_ <= 1400:
            self.transit_gait(tau=0)
        
        if self.count_ > 1800 and self.count_ <= 2000:
            self.transit_gait(tau=1)
        
        for _ in range(5):
            for i in np.arange(0, self.leg_num):
                r_pow = (self.leg_x[i] - self.u1) ** 2 + (self.leg_y[i] - self.u2) ** 2
                W = math.pi / (self._beta*self._t*(math.exp(-self._a*self.leg_y[i]) + 1)) + math.pi / ((1-self._beta)*self._t*(math.exp(self._a*self.leg_y[i]) + 1))
                V = np.matmul(np.array([[self._alpha * (self.mu_ - r_pow), - W], [W, self._alpha * (self.mu_ - r_pow)]]),
                            np.array([[self.leg_x[i] - self.u1], [self.leg_y[i] - self.u2]])) + \
                    np.matmul(self.R_cell[0, i], np.array([[self.leg_x[0] - self.u1], [self.leg_y[0] - self.u1]])) + \
                    np.matmul(self.R_cell[1, i], np.array([[self.leg_x[1] - self.u2], [self.leg_y[1] - self.u2]])) + \
                    np.matmul(self.R_cell[2, i], np.array([[self.leg_x[2] - self.u1], [self.leg_y[2] - self.u2]])) + \
                    np.matmul(self.R_cell[3, i], np.array([[self.leg_x[3] - self.u1], [self.leg_y[3] - self.u2]]))
                
                self.leg_x[i] = self.leg_x[i] + V[0, 0] * self.t_step
                self.leg_y[i] = self.leg_y[i] + V[1, 0] * self.t_step

        for i in range(0, self.leg_num):
            self.point_x[i] = self.leg_x[i]
            
            self.point_y[i] = self.leg_y[i]
        
            if self.leg_y[i] > 0:
                self.point_y[i] = 0
            else:
                self.point_y[i] = -self.leg_y[i]
            

        return np.concatenate([[h, k] for h, k in zip(self.point_x, self.point_y)])


if __name__ == '__main__':
    cpg = CPG(0)
    step_num = 1800
    
    plt.rcParams.update({'font.size': 20})

    fig1 = plt.figure(figsize=(9, 6))
    plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=None, hspace=0.5)

    phases = np.stack(np.array([cpg.step() for _ in range(step_num)]), axis=1)
    
    ax = plt.subplot(4, 1, 1)
    leg_labels = ['FL', 'FR', 'HL', 'HR']
    for i in range(4):
        ax.plot(np.arange(0, step_num) * 0.005, phases[2 * i, :], linewidth=2, label=leg_labels[i])
    
    ax.set_xlim(0,step_num * 0.005)
    ax.legend(prop={'size': 14}, loc= 'lower right')
    
    plt.show()

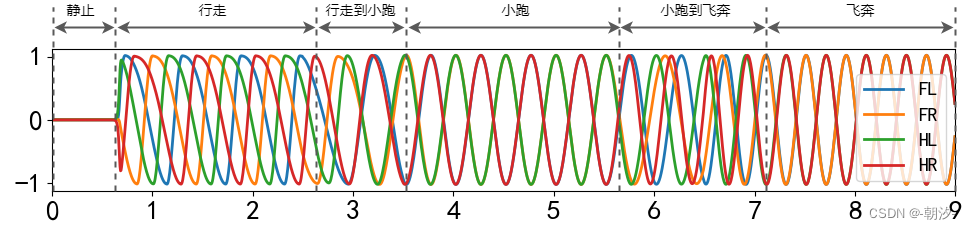
代码实现了从静止到行走（walk）到小跑（trot）再到飞奔（gallop）步态的转换。具体实现细节和解释有时间再写👌。

 相关文章：raisimGymTorch的使用-CSDN博客