Ural 大学有 N
名职员，编号为 1∼N
。

他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。

每个职员有一个快乐指数，用整数 Hi
给出，其中 1≤i≤N
。

现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。

在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

输入格式
第一行一个整数 N
。

接下来 N
行，第 i
行表示 i
号职员的快乐指数 Hi
。

接下来 N−1
行，每行输入一对整数 L,K
，表示 K
是 L
的直接上司。（注意一下，后一个数是前一个数的父节点，不要搞反）。

输出格式
输出最大的快乐指数。

数据范围
1≤N≤6000
,
−128≤Hi≤127
输入样例：
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
输出样例：
5

DFS 遍历树，求解每个节点的状态。
dfs 函数的参数 u 表示当前处理的节点。
遍历节点 u 的所有儿子节点，对每个儿子节点执行 DFS。
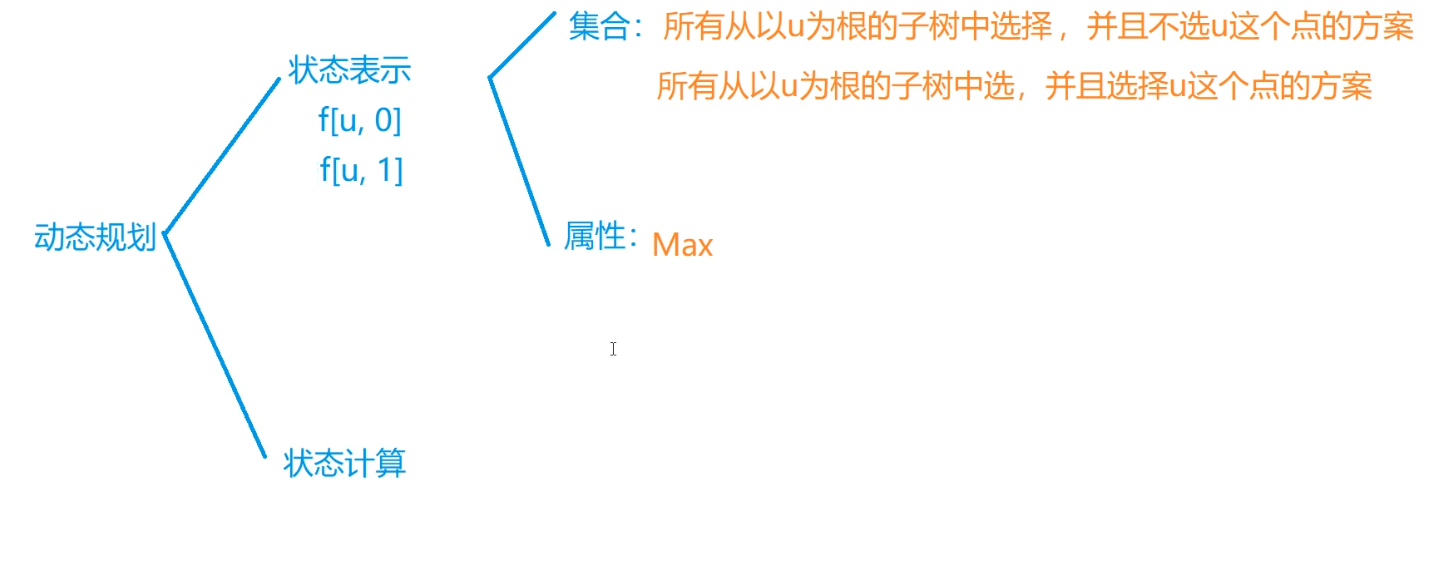
在递归过程中，更新状态 f[u][0] 和 f[u][1]：
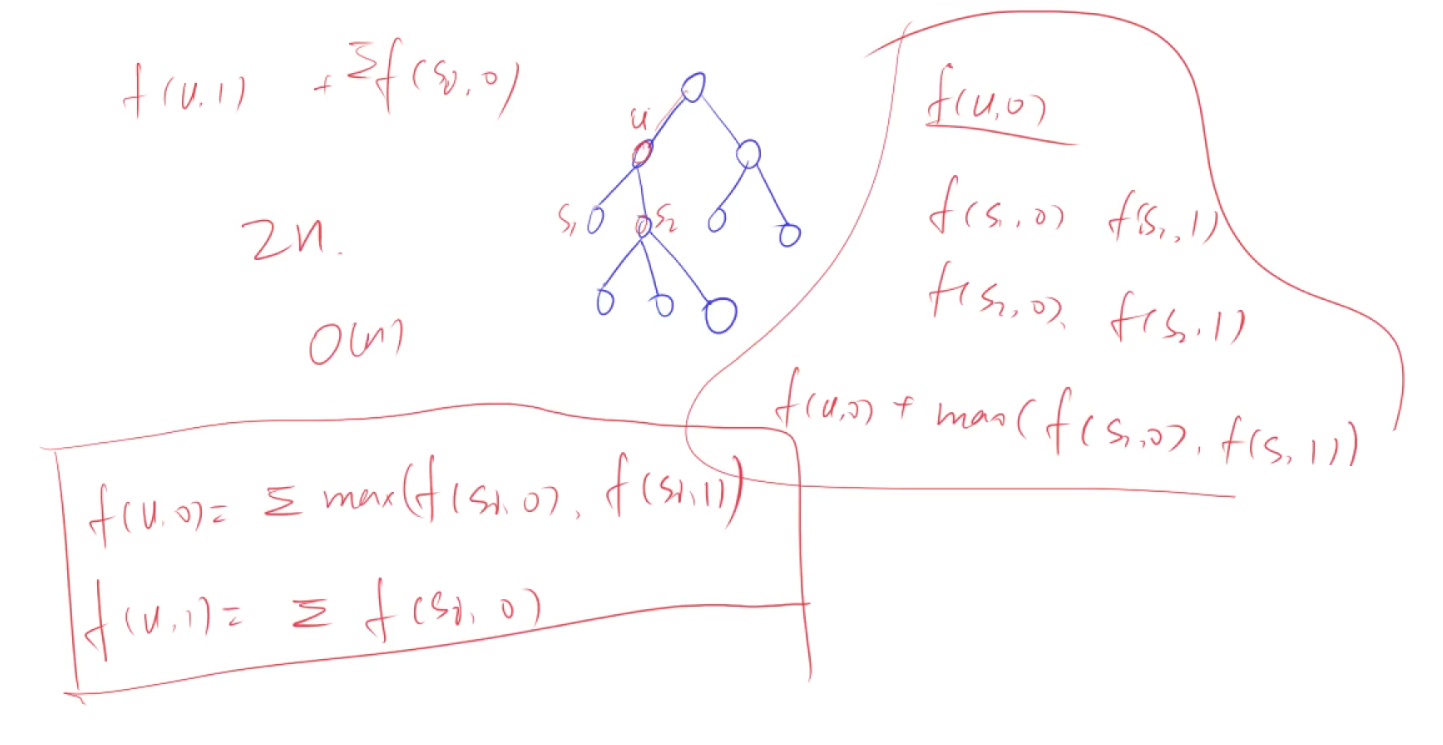
如果节点 u 不参加舞会，其最大快乐值为其所有儿子节点参加舞会和不参加舞会情况下的最大值之和。
如果节点 u 参加舞会，其最大快乐值为其所有儿子节点不参加舞会情况下的最大值之和，加上节点 u 的快乐值。
递归的边界条件是叶子节点，即没有儿子节点的节点。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 6010;
int n;
int happy[N];
int h[N], e[N], ne[N], idx; // 邻接表来存图
int f[N][2]; // 状态
bool has_father[N]; // 标记根节点

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void dfs(int u) // 递归求每一个状态
{
    f[u][1] = happy[u]; // f[u][1] 表示选择u这个点，就先把它加上
    
    for(int i = h[u]; i != -1; i = ne[i]) // 枚举u的所有儿子
    {
        int j = e[i]; // j表示u的每个儿子
        dfs(j); // 递归的算一下
        
        f[u][0] += max(f[j][0], f[j][1]); // 状态计算
        f[u][1] += f[j][0];
    }
}

int main ()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++ ) scanf("%d", &happy[i]);
    
    memset(h, -1, sizeof h);
    for(int i = 0; i < n - 1; i ++ )  // 读入每一条边
    {
        int a, b;
        scanf("%d%d", &a, &b);
        has_father[a] = true;
        add(b, a);
    }
    
    int root = 1;   // 枚举寻找根节点
    while(has_father[root]) root ++ ;
    
    dfs(root);
    
    cout << max(f[root][0], f[root][1]) << endl; // 只有两种情况，取根节点和不取，去一个max就是最终的答案
    
    return 0;
}