在建模问题或项目中,通常情况下,可接受模型的函数形式会以某种方式受到约束。这可能是由于业务考虑,或者由于正在研究的科学问题的类型。在某些情况下,如果对真实关系有非常强烈的先验信念,可以使用约束来提高模型的预测性能。
在这种情况下的一种常见约束类型是,某些特征与预测响应呈单调关系:
f ( x 1 , x 2 , … , x , … , x n − 1 , x n ) ≤ f ( x 1 , x 2 , … , x ′ , … , x n − 1 , x n ) f(x_1, x_2, \ldots, x, \ldots, x_{n-1}, x_n) \leq f(x_1, x_2, \ldots, x', \ldots, x_{n-1}, x_n) f(x1,x2,…,x,…,xn−1,xn)≤f(x1,x2,…,x′,…,xn−1,xn)
无论何时 x ≤ x ′ x \leq x' x≤x′是一个增加约束;或者
f ( x 1 , x 2 , … , x , … , x n − 1 , x n ) ≥ f ( x 1 , x 2 , … , x ′ , … , x n − 1 , x n ) f(x_1, x_2, \ldots, x, \ldots, x_{n-1}, x_n) \geq f(x_1, x_2, \ldots, x', \ldots, x_{n-1}, x_n) f(x1,x2,…,x,…,xn−1,xn)≥f(x1,x2,…,x′,…,xn−1,xn)
无论何时 x ≤ x ′ x \leq x' x≤x′是一个递减约束;
XGBoost具有对增强模型中使用的任何特征执行单调性约束的能力。
简单示例
为了说明,创建一些模拟数据,其中包含两个特征和一个响应,符合以下方案
y = 5 x 1 + sin ( 10 π x 1 ) − 5 x 2 − cos ( 10 π x 2 ) + N ( 0 , 0.01 ) x 1 , x 2 ∈ [ 0 , 1 ] y = 5 x_1 + \sin(10 \pi x_1) - 5 x_2 - \cos(10 \pi x_2) + N(0, 0.01) x_1, x_2 \in [0, 1] y=5x1+sin(10πx1)−5x2−cos(10πx2)+N(0,0.01)x1,x2∈[0,1]
响应通常随着 x 1 x_1 x1特征的增加而增加,但叠加了正弦变化,导致真实效果是非单调的。对于 x 2 x_2 x2特征,变化是减小的,具有正弦变化。
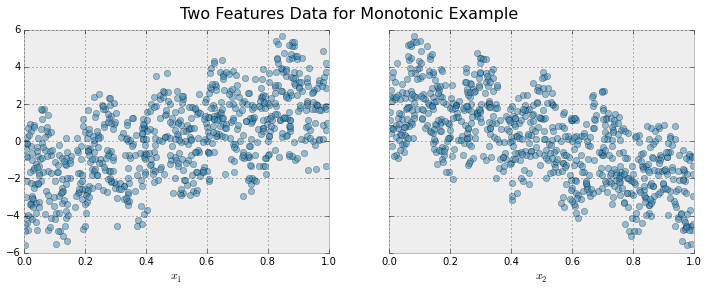
现在对这些数据进行拟合,而不施加任何单调性约束:
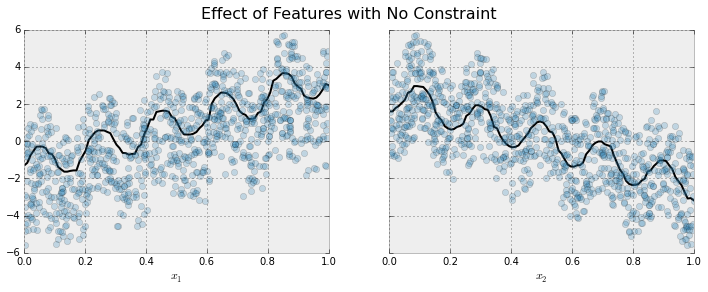
黑色曲线显示了从模型中推断出的每个特征的趋势。为了制作这些图,将突出显示的特征 x 1 x_1 x1传递给模型,其值在一维网格上变化,而所有其他特征(在这种情况下只有一个其他特征)被设置为它们的平均值。可以看到该模型很好地捕捉了周期波动的总体趋势。
这是相同的模型,但使用了单调性约束进行拟合:
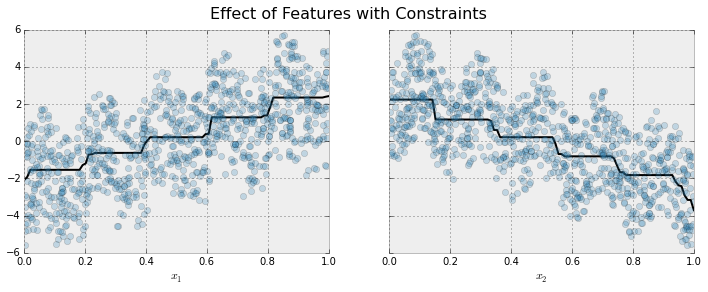
从上图可以看到约束的效果。对于每个变量,趋势的一般方向仍然明显,但振荡行为不再存在,因为这违反了强加的约束。
在 XGBoost 中强制执行单调约束
在XGBoost中强制执行单调性约束非常简单。这里将使用Python进行示例,但相同的一般思想可以推广到其他平台。
假设以下代码在没有单调性约束的情况下拟合模型:
model_no_constraints = xgb.train(params, dtrain,
num_boost_round = 1000, evals = evallist,
early_stopping_rounds = 10)
然后拟合单调性约束只需要添加单个参数
params_constrained = params.copy()
params_constrained['monotone_constraints'] = (1, -1)
model_with_constraints = xgb.train(params_constrained, dtrain,
num_boost_round = 1000, evals = evallist,
early_stopping_rounds = 10)
在这个例子中,训练数据 X 有两列,通过使用参数值 (1,-1),告诉 XGBoost 对第一个预测器施加递增约束,并对第二个预测器施加递减约束。
其他一些例子:
- (1, 0): 对第一个预测器施加递增约束,对第二个预测器没有约束
- (0, -1): 对第一个预测器没有约束,对第二个预测器施加递减约束
注意
‘hist’ tree construction algorithm的注意事项。如果将tree_method设置为hist或approx,启用单调性约束可能会导致树变得不必要地浅。这是因为hist方法减少了在每个分裂处考虑的候选分裂数。单调性约束可能会清除所有可用的分裂候选项,如果发生这种情况,将不会进行分裂。为减少影响,可能需要增加max_bin参数以考虑更多的分裂候选项。
使用特征名称
XGBoost的Python包支持使用特征名称而不是特征索引来指定约束。假设有一个包含列
[
"
f
0
"
,
"
f
1
"
,
"
f
2
"
]
["f0", "f1", "f2"]
["f0","f1","f2"]的数据框,可以将单调性约束指定为
"
f
0
"
:
1
,
"
f
2
"
:
−
1
{"f0": 1, "f2": -1}
"f0":1,"f2":−1,而"f1"将默认为0(无约束)。
import xgboost as xgb
import numpy as np
import matplotlib.pyplot as plt
# Simulated data
np.random.seed(42)
num_samples = 1000
X = np.random.rand(num_samples, 2)
def calculate_y(X):
x1 = X[:, 0]
x2 = X[:, 1]
return 5 * x1 + np.sin(10 * np.pi * x1) - 5 * x2 - np.cos(10 * np.pi * x2) + np.random.normal(0, 0.01, len(X))
y = calculate_y(X)
# Fitting a model without monotonicity constraints
params = {'objective': 'reg:squarederror', 'booster': 'gbtree'}
model = xgb.XGBRegressor(**params)
model.fit(X, y)
y_pred = model.predict(X)
# Fitting a model with monotonicity constraints
params_constrained = {'objective': 'reg:squarederror', 'booster': 'gbtree', 'monotone_constraints': '(1, -1)'}
model_constrained = xgb.XGBRegressor(**params_constrained)
model_constrained.fit(X, y)
y_constrained_pred = model_constrained.predict(X)
fig, axs = plt.subplots(2, 2, figsize=(12, 10))
axs[0, 0].scatter(X[:, 0], y_pred)
axs[0, 0].set_xlabel('X1')
axs[0, 0].set_ylabel('Y')
axs[0, 0].set_title('X1-Y Relationship')
axs[0, 1].scatter(X[:, 1], y_pred)
axs[0, 1].set_xlabel('X2')
axs[0, 1].set_ylabel('Y')
axs[0, 1].set_title('X2-Y Relationship')
axs[1, 0].scatter(X[:, 0], y_constrained_pred)
axs[1, 0].set_xlabel('X1')
axs[1, 0].set_ylabel('Y')
axs[1, 0].set_title('X1-Y constraints Relationship')
axs[1, 1].scatter(X[:, 1], y_constrained_pred)
axs[1, 1].set_xlabel('X2')
axs[1, 1].set_ylabel('Y')
axs[1, 1].set_title('X2-Y constraints Relationship')
plt.tight_layout()
plt.show()
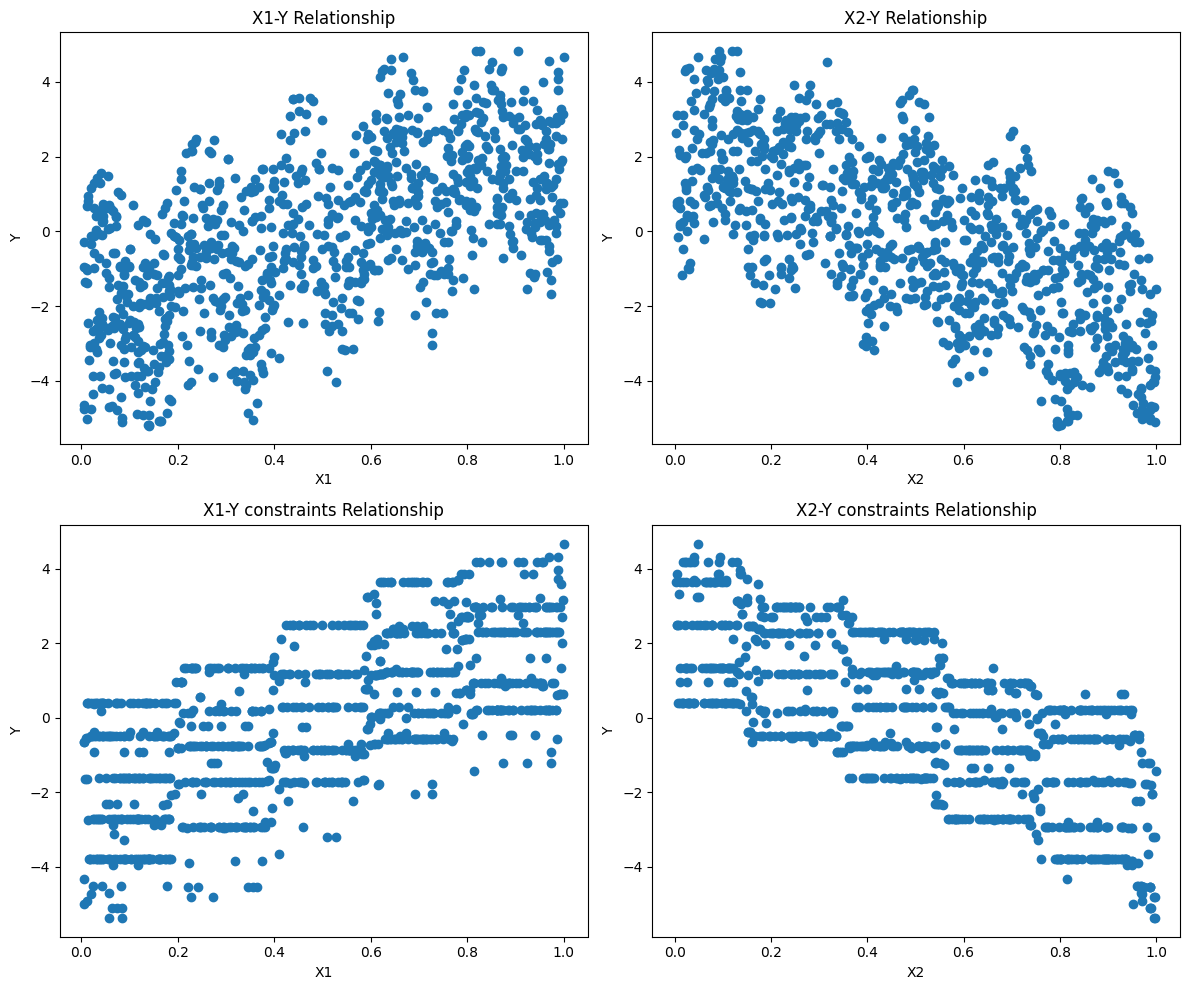
参考
- https://xgboost.readthedocs.io/en/latest/tutorials/monotonic.html