前言：做这个实验的时候很忙，就都是你抄我我抄你了

一、基础知识

1．为什么要进行图像压缩：
图像的数据量巨大，对计算机的处理速度、存储容量要求高。传输信道带宽、通信链路容量一定，需要减少传输数据量，提高通信速度。因此要进行图像压缩，减少数据量。
2．怎么进行图像压缩：
我们使用霍夫曼编码进行压缩。霍夫曼编码原理是利用信息符号概率分布特性的变字长的编码方法。对于出现概率大的信息符号编以短字长的码，对于出现概率小的信息符号编以长字长的码。

二、实验要求

1．读入一幅灰度图像，计算该图像的平均信息量-熵。
（备注：可以读入小一些的图像，例如256256，512512的。）
2．使用霍夫曼编码的方法，对该图像进行压缩。
3. 计算编码后的平均码长及压缩比。

三、实验记录

任务1：

读入一幅灰度图像，计算该图像的平均信息量-熵。
（备注：可以读入小一些的图像，例如256256，512512的。）

%求一幅图像的熵值
clc
clear
close all
I=imread('Acat.png');
I = rgb2gray(I);


G=256; %图像的灰度级
[height,width] = size(I); %获取输入值的高和宽
[count,x] = imhist(I,G);
p = count; %原始灰度直方图
I_size = height*width;
H_x = 0;
for i=1:256  %循环
    p(i) = count(i)/I_size;
    if p(i)~=0; %如果像素点的概率不为零
        H_x=-p(i)*log2(p(i))+H_x; %求熵值的公式
    end
end
H_x  %显示熵值

任务2：

使用霍夫曼编码的方法，对该图像进行压缩。

[M,N] = size(I);%将图像转为二维矩阵
I1 = I(:);%转为一维向量
k = 0:255;
dict = huffmandict(k,p); %根据灰度级k和概率数组P生成Huffman字典
enco = huffmanenco(I1,dict); 
deco = huffmandeco(enco,dict); %哈夫曼解码
Ide = col2im(deco,[M,N],[M,N],'distinct'); %把向量重新转换成图像块；
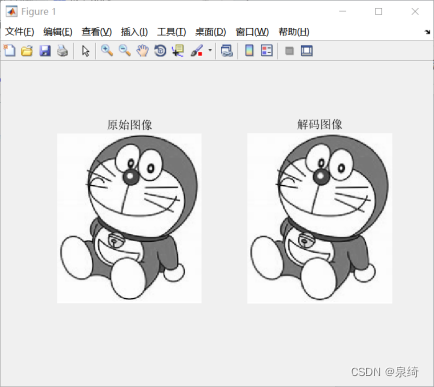
subplot(1,2,1);imshow(I);title('原始图像');
subplot(1,2,2);imshow(uint8(Ide));title('解码图像');

任务3：

计算编码后的平均码长及压缩比。

B=length(enco);
sumcode=length(deco);%编码后比特长度
CR=sumcode/B;%计算压缩率
disp(['原始图像 Bit: ',num2str(B),' bit']);
disp(['压缩图像 Bit: ',num2str(sumcode),' bit']);
disp(['压缩率: ',num2str(CR)]);

四、实验结果

任务1：

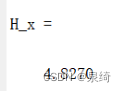
任务2：

任务3：