参考:
多元函数的偏导数、方向导数、梯度以及微分之间的关系思考 - 知乎
关于梯度下降与Momentum通俗易懂的解释_ssswill的博客-CSDN博客_有momentum之后还要梯度剪裁吗
前言:
这里简单了解一下 导数 梯度 微分的概念。
在前面矩阵求导术里面介绍过 梯度与微分的关系,通过该映射关系
可以得到损失函数的梯度.
目录:
1 导数
2 微分
3 梯度
4 影响局部极小值|鞍点的因素
一 导数
1.1 一元函数导数: 标量
定义: 导数描述的是函数在一点处的变化快慢的趋势,是一个变化的速率
例:
其导数为 2x
1.2 多元函数:偏导数(标量)
多元函数降维时候的变化,比如二元函数固定y,只让x单独变化,从而看成是关于x的一元函数的变化来研究。

1.3 方向导数:
本质就是函数在A点无数个切线的斜率的定义.每一个切线都代表一个变化的方向.
二 微分
微分:标量
描述的是函数从一点(移动一个无穷小量)到另一点的变化幅度,是一个变化的量。
全微分:函数从A点到B点变化的量(其实是取一个无穷小的变化的量)

例
全微分:
三 梯度(gradient)
梯度:向量
函数在A点无数个变化方向中变化最快的那个方向.
在深度学习中 梯度更新的常用公式为
Function:
Objective:
update rule:
Derivates:
四 影响局部极小值|鞍点的因素
深度学习中网络深度比较深,loss 常常会陷入到局部极小值或者鞍点中。
4.1 Initialization status
如下图 当初始值分别为 A,B 两个点。 B点搜索更容易陷入局部极小值
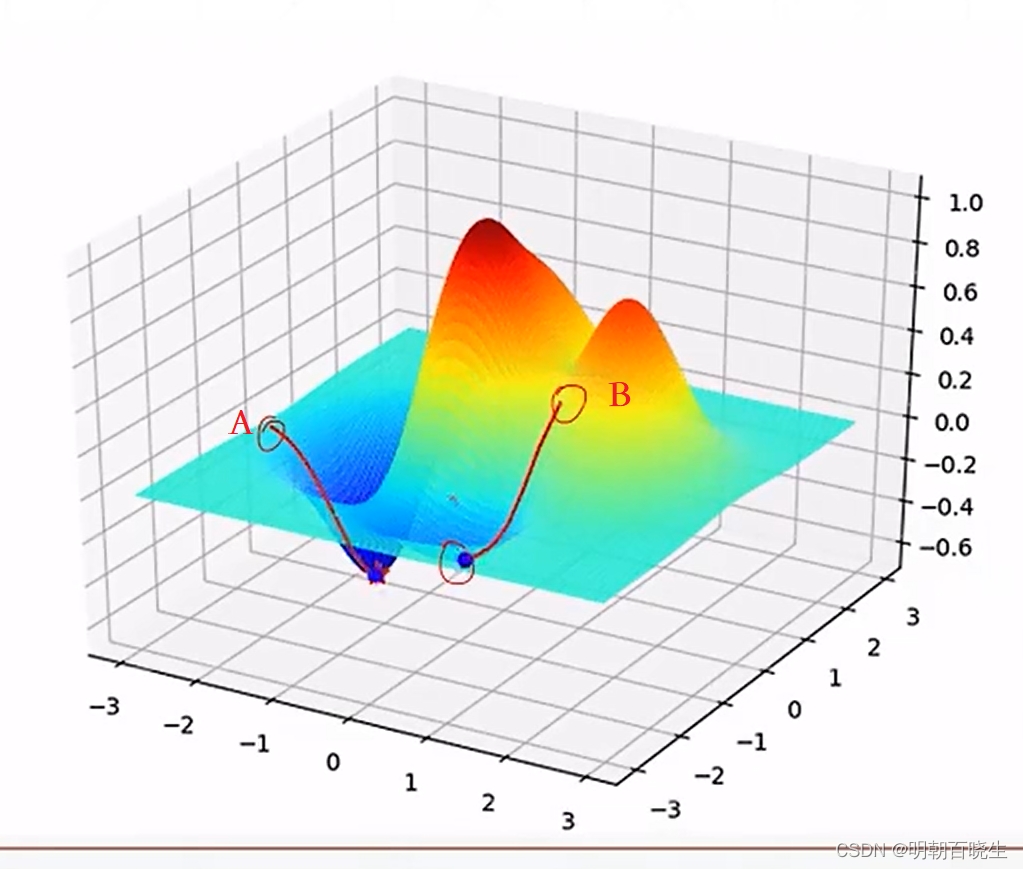
4.2 Learn Rate
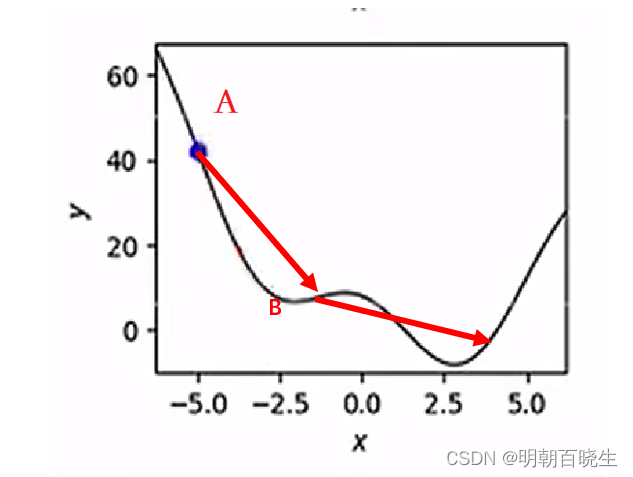
如下图 当学习率过大的时候,很难搜索到全局最小点
过小的时候容易进入局部最小点B, 一般设置为0.01,0.05
4.3 Momentum
SGD 参数更新过程:
问题:
-
学习率较小时,收敛到极值的速度较慢。
-
学习率较大时,容易在搜索过程中发生震荡
解决方案:
动量因子
参数更新过程: