相关推荐
python coding with ChatGPT 打卡第12天| 二叉树：理论基础
python coding with ChatGPT 打卡第13天| 二叉树的深度优先遍历
python coding with ChatGPT 打卡第14天| 二叉树的广度优先遍历
python coding with ChatGPT 打卡第15天| 二叉树：翻转二叉树、对称二叉树
python coding with ChatGPT 打卡第16天| 二叉树：完全二叉树、平衡二叉树、二叉树的所有路径、左叶子之和
python coding with ChatGPT 打卡第17天| 二叉树：找树左下角的值、路径总和

从中序与后序遍历序列构造二叉树

Key Points

1. 以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。
2. 如何使用切割后的后序数组来切合中序数组？利用中序数组大小一定是和后序数组的大小相同这一特点来进行切割。

相关题目

106. 从中序与后序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树

视频讲解

来看看你掉到几次坑

重点分析

def buildTree(inorder, postorder):
    if not postorder:
        return None
    root = TreeNode(postorder[-1])
    in_root_index = inorder.index(root.val)
    in_left = inorder[:in_root_index]
    in_right = inorder[(in_root_index+1):]
    post_left = postorder[:len(in_left)]
    post_right = postorder[len(in_left):-1]

    root.left = buildTree(in_left, post_left)
    root.right = buildTree(in_right, post_right)
    return root

def buildTree(preorder, inorder):
    if not preorder:
        return None
    
    # 创建根节点
    root = TreeNode(preorder[0])
    
    # 在中序遍历中找到根节点的索引，分割中序遍历
    in_root_index = inorder.index(root.val)
    in_left = inorder[:in_root_index]
    in_right = inorder[in_root_index+1:]
    
    # 分割先序遍历
    pre_left = preorder[1:1+len(in_left)]
    pre_right = preorder[1+len(in_left):] 

    # 递归构建左右子树
    root.left = buildTree(pre_left, in_left)
    root.right = buildTree(pre_right, in_right)

    return root

拓展

前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。
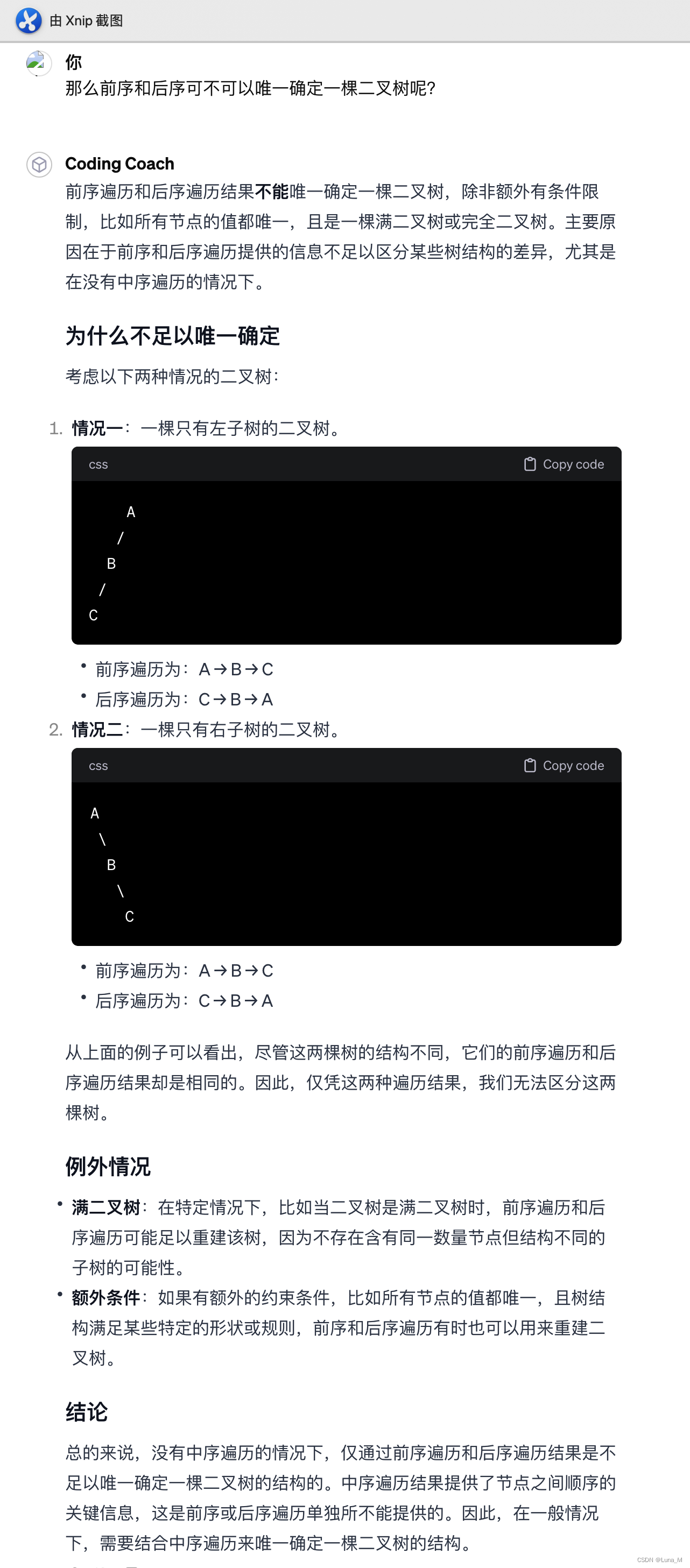
那么前序和后序可不可以唯一确定一棵二叉树呢？

最大二叉树

Key Points

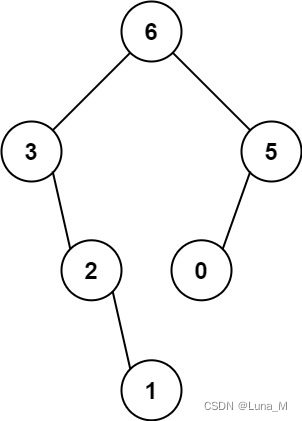递归调用如下所示：

• [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
  • [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
    • 空数组，无子节点。
    • [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
      • 空数组，无子节点。
      • 只有一个元素，所以子节点是一个值为 1 的节点。
  • [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
    • 只有一个元素，所以子节点是一个值为 0 的节点。
    • 空数组，无子节点。

相关题目

654. 最大二叉树

视频讲解

又是构造二叉树

重点分析

def constructMaximumBinaryTree(nums):
    if not nums:
        return None
    root_val = max(nums)
    root = TreeNode(root_val)
    root_index = nums.index(root_val)
    left = nums[:root_index]
    right = nums[root_index+1:]
    root.left = constructMaximumBinaryTree(left)
    root.right = constructMaximumBinaryTree(right)
    return root