力扣刷题之旅:进阶篇(二)
继续我的力扣刷题之旅,我在进阶篇的第一部分中深入探索了BFS(广度优先搜索)算法,并感受到了它在图形搜索中的强大威力。现在,我进入了进阶篇的第二部分,准备迎接更多挑战和机遇。
一、深入图算法
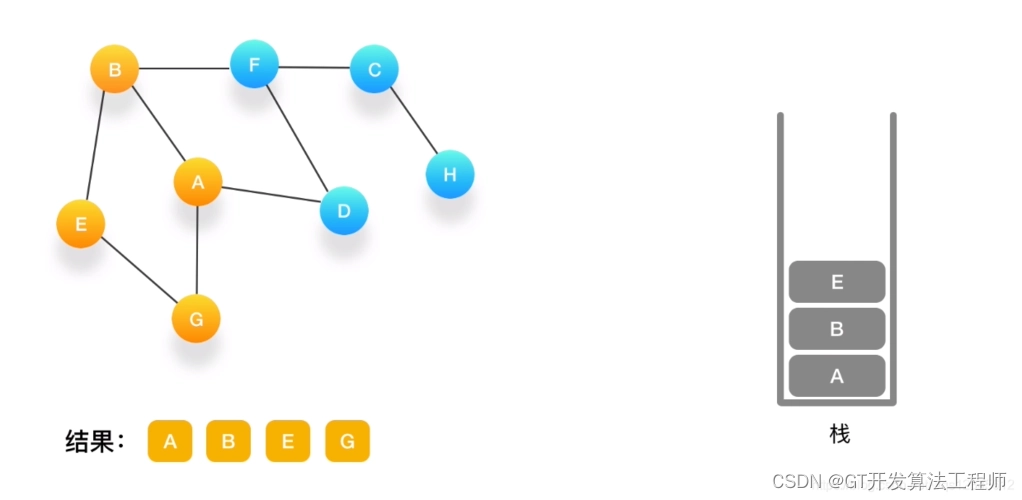
在进阶篇的第二部分,我更加深入地研究了图算法。除了BFS,我还学习了DFS(深度优先搜索)算法,并对比了它与BFS的不同之处。DFS是一种用于遍历或搜索树或图的算法,它沿着树的深度遍历树的节点,直到达到目标节点或遍历完所有节点。
通过对比BFS和DFS,我发现了它们在应用场景上的区别。BFS适用于寻找最短路径、查找最近邻节点等问题,而DFS则更适用于解决需要深入搜索的问题,如寻找图中的环、判断二叉树是否为平衡树等。
此外,我还学习了其他图算法,如拓扑排序、最小生成树等。这些算法在图论中有着广泛的应用,如网络优化、社交网络分析、图像处理等。
二、动态规划的进阶
在进阶篇的第一部分中,我已经初步了解了动态规划的基本概念和应用。在第二部分中,我进一步深入学习了动态规划的高级技巧和优化方法。
我学习了如何运用动态规划解决一些更复杂的问题,如背包问题、最长递增子序列等。在解决这些问题的过程中,我不断尝试优化状态转移方程,减少重复计算,提高算法的效率。
同时,我还学习了动态规划的空间优化技巧,如滚动数组等。这些技巧可以帮助我们减少算法的空间复杂度,提高代码的运行效率。
三、算法设计与分析
在进阶篇的第二部分,我还开始接触算法设计与分析的相关知识。我学习了如何根据问题的特点选择合适的算法,并对算法的性能进行分析和评估。
我学习了算法的时间复杂度和空间复杂度的概念和分析方法,了解了如何通过优化算法来降低时间复杂度和空间复杂度。同时,我还学习了算法的正确性证明和复杂度证明等相关知识。
四、未来的展望
在进阶篇的第二部分中,我取得了很大的进步,但也遇到了很多挑战和困难。我相信,在未来的刷题之旅中,我会继续努力,不断突破自己,掌握更多的算法和数据结构。
同时,我也希望能够与更多的编程爱好者一起交流和分享刷题经验,共同进步。我相信,在力扣这个平台上,我们可以相互学习、相互鼓励,成为更好的编程师。
总的来说,力扣的刷题之旅是一次充满挑战和收获的旅程。通过不断学习和实践,我不仅提升了自己的编程技能,还培养了自己的逻辑思维和解决问题的能力。在未来的日子里,我会继续坚持刷题,探索更多的算法和数据结构,为自己的编程之路不断添砖加瓦。
from collections import deque
def bfs(graph, start):
visited = set()
queue = deque([start])
while queue:
vertex = queue.popleft()
print(vertex, end=" ")
for neighbor in graph[vertex]:
if neighbor not in visited:
visited.add(neighbor)
queue.append(neighbor)
# 示例图的邻接表表示
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E'],
}
bfs(graph, 'A') # 输出: A B C D E F