题目描述
一个如下的 6×66×6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。

上面的布局可以用序列 2 4 6 1 3 52 4 6 1 3 5 来描述,第 i 个数字表示在第 i 行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 61 2 3 4 5 6
列号 2 4 6 1 3 52 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 33 个解。最后一行是解的总个数。
输入格式
一行一个正整数 n,表示棋盘是 n×n 大小的。
输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
输入输出样例
输入
6
输出
2 4 6 1 3 5 3 6 2 5 1 4 4 1 5 2 6 3 4
说明/提示
【数据范围】
对于 100%的数据,6≤n≤13。
解题思路:
从每一行开始,遍历一这行的所有元素,如果这一行的列,正对角,反对角都没有皇后,就在这个位置放入一个皇后,然后继续向下一行进行搜索。
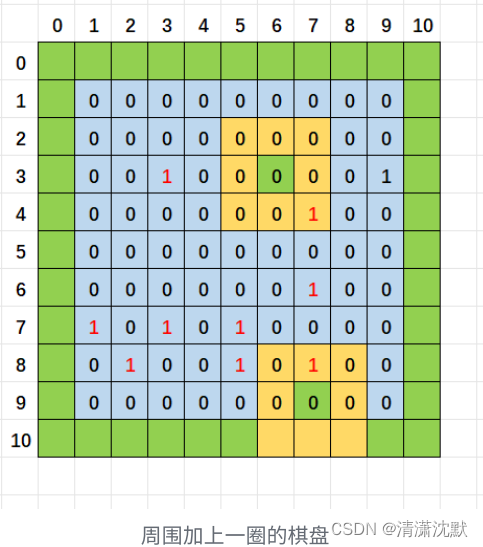
对角坐标如下图:

(蓝色为正对角,绿色为反对角,
故正对角线的坐标为:当前行+当前列,
反对角坐标为:n-当前行+当前列。
代码如下:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 20;
bool y[N], dg[N], udg[N]; //分别用于记录当前元素的这一列,正对角,反对角是否有元素
int n, ans;
int e[N][N];
void dfs(int u) //深度优先遍历
{
if (u == n) //当遍历到最后一行时结束
{
//如果成功搜索到最后一行,就说明已经找到了一个方案,就把这个方案输出
if (ans < 3) //只输出3次结果
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (e[i][j] == 1)
cout << j + 1 << " ";
}
}
cout << endl;
}
ans++; //记录一共几条结果满足条件
}
for (int i = 0; i < n; i++)
{
//遍历这一行当中得元素,如果这一列以及两个对角都没有皇后,就在这个坐标放入一个皇后
if (!y[i] && !dg[u + i] && !udg[n - u + i])
{
e[u][i] = 1;
y[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);//放完后继续向下一行搜索
//搜索完之后回溯要把数据还原
y[i] = dg[u + i] = udg[n - u + i] = false;
e[u][i] = 0;
}
}
}
int main()
{
cin >> n;
dfs(0);
cout << ans << endl;
return 0;
}模板题,可以看看n皇后dfs求解
n皇后问题(DFS)
算法小白的刷题日记。