目录
初识EM算法
马尔可夫链
HMM模型基础
HMM模型使用
初识EM算法
EM算法是一种求解含有隐变量的概率模型参数的迭代算法。该算法通过交替进行两个步骤:E步骤和M步骤,从而不断逼近模型的最优参数值。EM算法也称期望最大化算法,它是一个基础算法,是很多机器学习领域算法的基础,比如隐式马尔可夫算法(HMM)等等。
EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步:
其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法。
EM算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题,其算法基础和收敛有效性等问题,其基本思想是:
1)首先根据已经给出的观测数据,估计出模型参数的值
2)然后再依据上一步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计
3)然后反复迭代,直至最后收敛,迭代结束。
EM算法计算流程如下:

极大似然估计: 极大似然估计是一种常用的统计方法,用于从观测数据中估计概率模型的参数。它的基本思想是寻找在给定观测数据条件下使得概率模型产生观测数据的概率最大的参数值。
假如我们需要调查学校的男生和女生的身高分布,我们抽取100个男生和100个女生,将他们按照性别划分为两组。然后,统计抽样得到100个男生的身高数据和100个女生的身高数据。

我们知道样本所服从的概率分布模型和一些样本,我们需要求解该模型的参数,
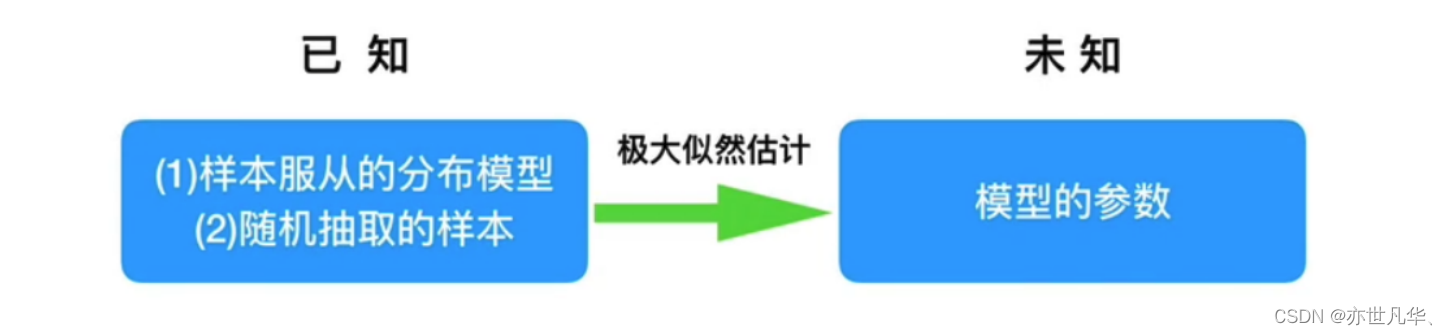
我们已知的条件有两个:
1)样本服从的分布模型 2)随机抽取的样本。
我们需要求解模型的参数,根据已知条件,通过极大似然估计,求出未知参数。
以下是最大似然函数估计值的求解步骤:

马尔可夫链
马尔可夫链(Markov Chain)是一种随机过程,通常用于建模具有“无记忆性”特征的序列数据。在马尔可夫链中,当前状态只取决于前一个状态,而与更早的状态无关。在机器学习算法中,马尔可夫链是个很重要的概念。又称离散时间马尔可夫链,因俄国群学家安德烈·马尔可夫得名。
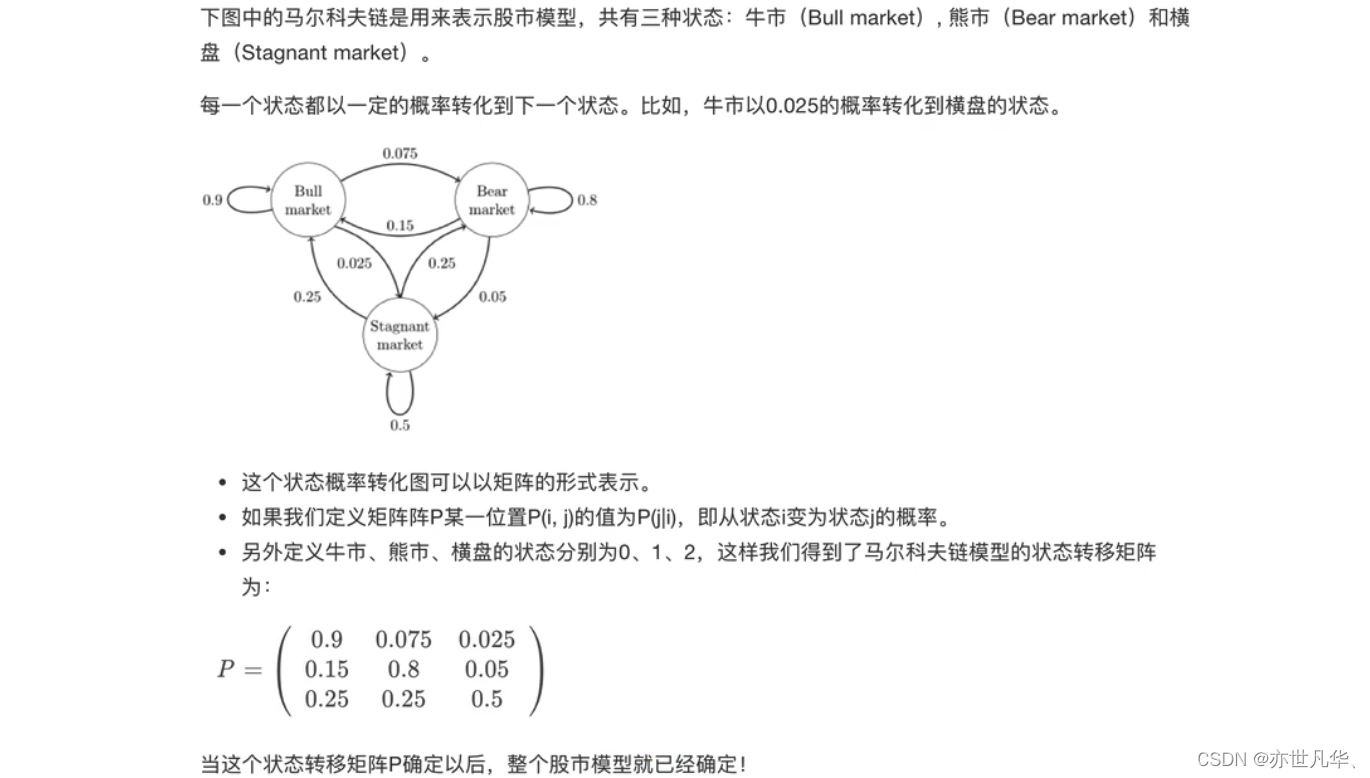
马尔可夫链即为状态空间中从一个状态到另一个状态转换的随机过程:

该过程要求具备“无记忆"的性质:下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性"称作马尔可夫性质。
马尔可夫链作为实际过程的统计模型具有许多应用,在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。态的改变叫做转多,与不同的状态改变相关的概率叫做转移概率。
马尔可夫链的数学表示如下:

某一时刻状态转移的概率只依赖前一个状态,那么只要求出系统中任意两个状态之间的转移概率,这个马尔可夫链的模型就定了。以下是马尔可夫链的经典案例:
HMM模型:隐马尔可夫模型是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。通过以下简单案例来介绍:



其实对于HMM来说,如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率,做模拟是相当容易的。但是应用HMM模型时候呢,往往是缺失了一部分信息的。和HMM模型相关的算法主要分为三类,分别解决三种问题:
1)知道般子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次掷出来的都是哪种般子(隐含状态链)。



2)还是知道骰子有几种(隐含状态数量),每种般子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。


3)知道骰子有几种(隐含状态数量),不知道每种般子是什么(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种般子是什么(转换概率)。




HMM模型基础
HMM模型是基于马尔可夫链的一种概率图模型,广泛应用于语音识别、自然语言处理、生物信息学等领域。与普通的马尔可夫链不同,HMM模型包含两个状态集合:观测状态集合和隐藏状态集合。观测状态表示我们可以直接观察到的状态,隐藏状态则表示我们无法直接观察到的状态。隐藏状态之间仍然满足马尔可夫性质,即当前状态只与前一个状态有关。
HMM模型做了两个很重要的假设如下:
齐次马尔科夫链假设:

观测独立性假设:

什么样的问题需要HMM模型?

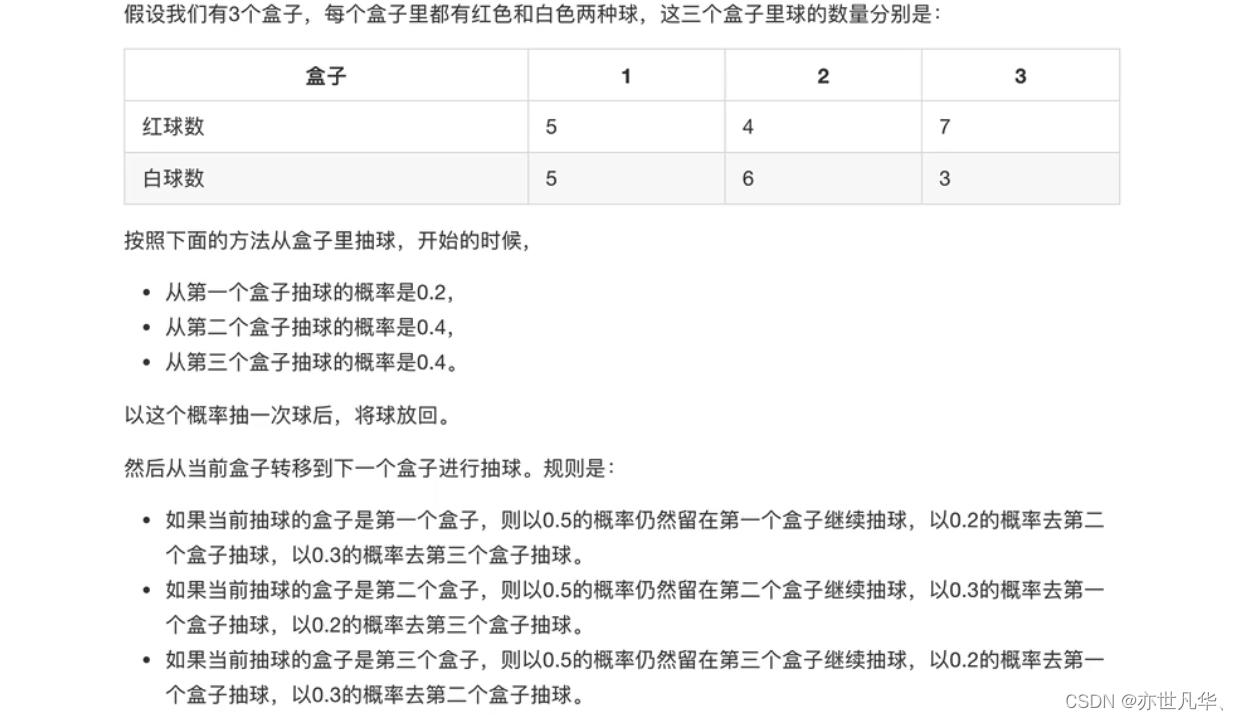
HMM模型实例:下面我们用一个简单的实例来描述上面抽象出的HMM模型。这是一个盒子与球的模型:

HMM观测序列的生成:

HMM模型的三个基本问题:

HMM模型使用
有多个库可以用来实现HMM模型,这里我就拿常用的hmmlearn库进行举例,hmmlearn是一个基于scikit-learn的Python库,提供了多种HMM模型及其变体的实现。它支持高斯混合模型和多项式分布模型,可以用于多个领域的序列学习问题。以下是其安装命令,终端执行如下命令安装:
pip install hmmlearn -i https://pypi.mirrors.ustc.edu.cn/simplehmmlearn实现了三种HMM模型类,按照观测状态是连续状态还是离散状态,可以分为两类。
GaussianHMM和GMMHMM是连续观测状态的HMM模型,而MultinomiaIHMM是离散观测状态的模型,也是我们在HMM原理系列篇里面使用的模型。在这里主要介绍我们前面一直讲的关于离散状态的MultinomialHMM模型。对于MultinomialHMM的模型,使用比较简单:
1)tartprob_"参数对应我们的隐藏状态初始分布Ⅱ。
2)transmat_"对应我们的状态转移矩阵A。
3)emissionprob_"对应我们的观测状态概率矩阵B。
以下是使用HMM模型的基础案例讲解:
# 导入相应模块
import numpy as np
from hmmlearn import hmm下面这段代码是一个使用隐马尔可夫模型进行建模的示例,这些参数的设定是HMM模型的基础,它们描述了隐藏状态和观测状态之间的关系。在实际应用中,你可以根据具体问题来设定这些参数,然后使用HMM模型进行概率计算、状态预测等任务:
# 设定隐藏状态的集合
states = ["box 1", "box 2", "box 3"]
n_states = len(states)
# 设定观察状态的集合
observations = ["red", "white"]
n_observations = len(observations)
# 设定初始状态分布
start_probability = np.array([0.2, 0.4, 0.4])
# 设定状态转移概率分布矩阵
transition_probability = np.array([[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]])
# 设定观测状态概率矩阵
emission_probability = np.array([[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]])下面这段代码是使用hmmlearn库中的CategoricalHMM模型来进行隐马尔可夫模型建模的示例,利用这个已经初始化好的模型对象进行概率计算、状态预测等任务。这里的CategoricalHMM模型是用于处理离散观测状态的情况,如果观测状态是连续值,可以考虑使用GaussianHMM模型:
# 定义模型
model = hmm.CategoricalHMM(n_components=n_states)
# 设定模型参数
model.startprob_ = start_probability # 初始化状态分布
model.transmat_ = transition_probability # 初始化状态转移概率分布矩阵
model.emissionprob_ = emission_probability # 初始化观测状态概率矩阵对于 HMM 问题三:维特比算法的解码过程,使用和之前一样的观测序列来解码:

# 维特比模型训练
box = model.predict(seen)
print("球的观测顺序为:", ' → '.join(map(lambda x: observations[x], seen.flatten())))
# 注意:需要使用flatten方法,把seen从二维变成一维
print("最可能的隐藏状态序列为:", ' → '.join(map(lambda x: states[x], box)))得到的结果如下所示:

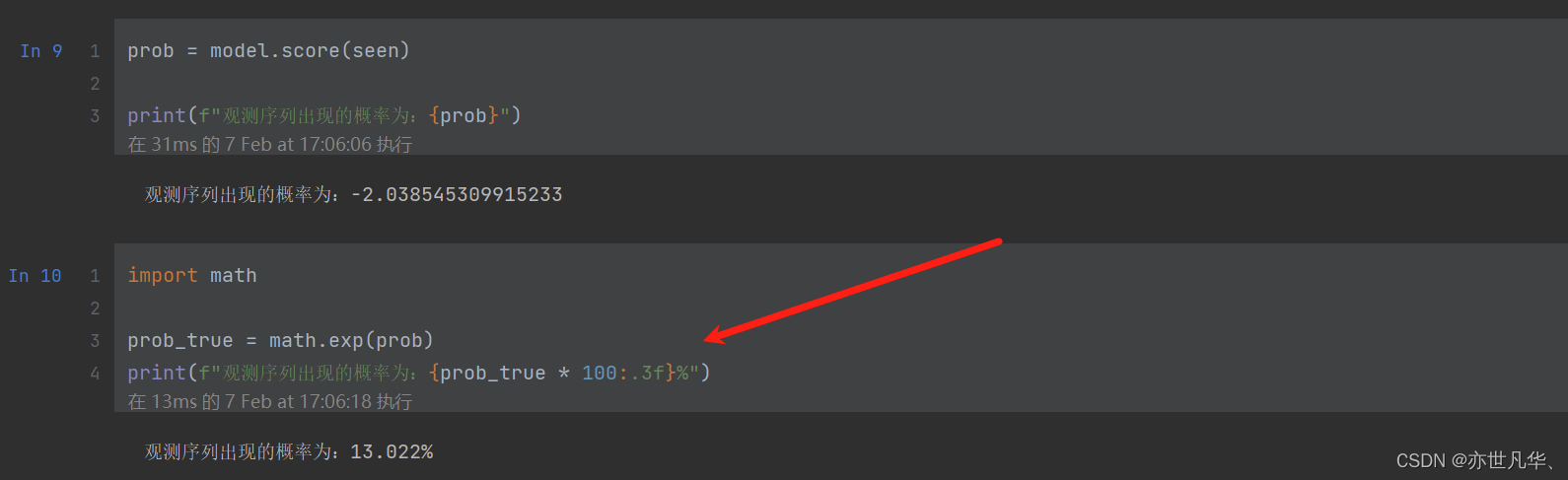
如果求 HMM 问题一的观测序列的概率的问题,代码如下: