LeetCode 93.复原IP地址
LeetCode 78.子集
LeetCode 90.子集II

复原IP地址

一些字符串的基本操作不会

s.insert(i + 1, ‘.’);

s.deleteCharAt(i + 1);

class Solution {

    List<String> result = new ArrayList<>();

    public List<String> restoreIpAddresses(String s) {
        StringBuilder sb = new StringBuilder(s);   // 注意  StringBuilder(s)
        backtracking(sb, 0, 0);
        return result;
    }

    private void backtracking(StringBuilder s, int startIndex, int pointNum) {
        if (pointNum == 3) {
            if (isValid(s, startIndex, s.length() - 1)) { // 结束条件
                result.add(s.toString());
            }
            return;
        }
        
        for (int i = startIndex; i < s.length(); i++) {
            if (isValid(s, startIndex, i)) {
                s.insert(i + 1, '.');
                backtracking(s, i + 2, pointNum + 1);
                s.deleteCharAt(i + 1);
            } else {
                break;
            }
        }
    }

    private boolean isValid(StringBuilder s, int start, int end) {
        if (start > end) {
            return false;
        }
        if (s.charAt(start) == '0' && start != end) {// 0开头的数字不合法
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            if (s.charAt(i) > '9' || s.charAt(i) < '0') {
                return false;
            }
            num = num * 10 + (s.charAt(i) - '0');
            if (num > 255) {// 如果⼤于255了不合法
                return false;
            }
        }
        return true;
    }
}

子集

组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

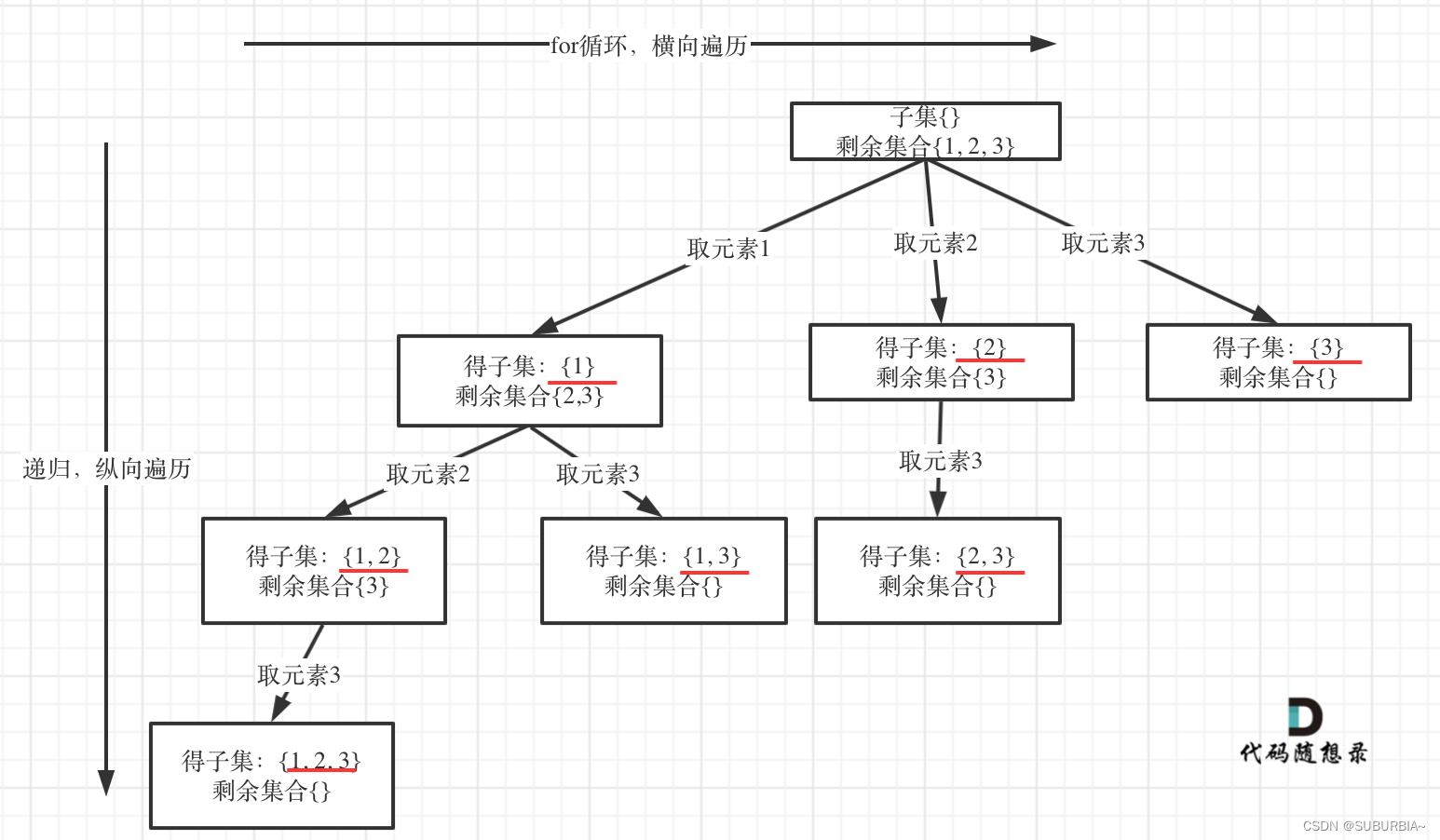
遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合。

求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。

result.add(new ArrayList<>(path)); // 放在终止条件的外面

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        backTracking(nums, 0);
        return result;
    }   

    private void backTracking(int[] nums, int startIndex) {
        result.add(new ArrayList<>(path));   // 最重要的一步，遍历整棵树，获取所有节点
        if (startIndex >= nums.length) {  //终止条件可不加
            return;
        }
        for (int i = startIndex; i < nums.length; i++) {
            path.add(nums[i]);
            backTracking(nums, i + 1);
            path.removeLast();
        }
    }
}

子集 II

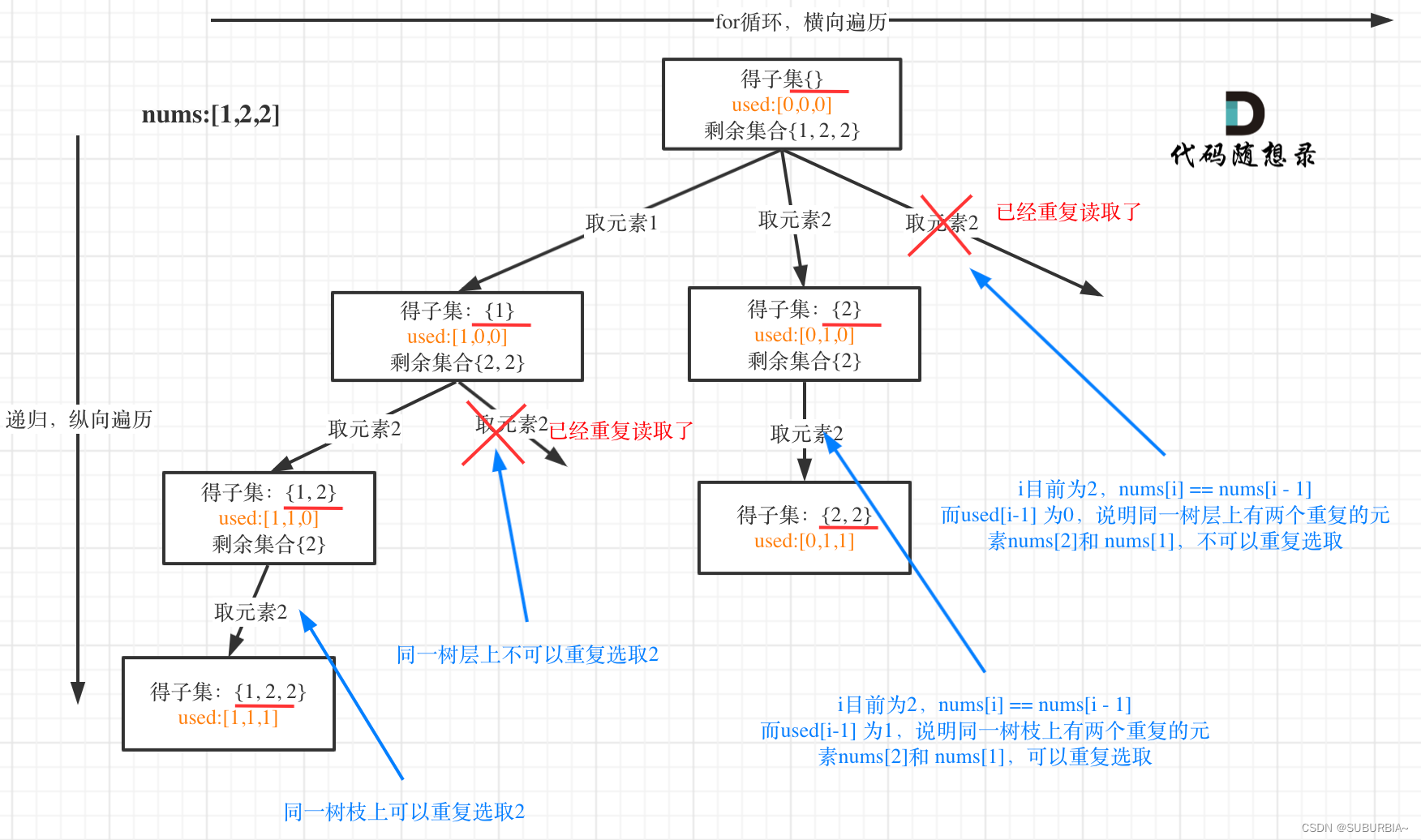
重点： 排序、i > startIndex
跳过当前树层使用过的、相同的元素

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backTracking(nums, 0);
        return result;
    }

    private void backTracking(int[] nums, int startIndex) {
        result.add(new ArrayList<>(path));

        if (startIndex >= nums.length) return;

        for (int i = startIndex; i < nums.length; i++) {
            // 跳过当前树层使用过的、相同的元素
            if (i > startIndex && nums[i] == nums[i - 1]) {
                // path.removeLast();
                continue;
            }
            path.add(nums[i]);
            backTracking(nums, i + 1);
            path.removeLast();
        }
    }
}