个人主页:PingdiGuo_guo
收录专栏:C++干货专栏

大家好,我是PingdiGuo_guo,今天我们来学习二维数组。
文章目录
1.二维数组的概念与思想
2.二维数组和一维数组的区别
3.二维数组的特点
4.二维数组的操作
1.定义
2.初始化
1.直接赋值
2.动态赋值
3.输出
1.直接输出
2.动态输出
4.遍历
5.排序
1.使用STL库函数
2.手写排序算法
6.插入
1.在头部插入
2.在中间插入
3.在尾部插入
5.练习
6.总结
1.二维数组的概念与思想
二维数组是一种数据结构,它可以存储具有多个维度的数据元素。它是由多个一维数组组成的,每个一维数组都可以看作是二维数组的一行。
二维数组的思想是将数据元素按照行和列的方式排列,通过使用两个索引可以定位到二维数组中的任意一个元素。其中,第一个索引表示行号,第二个索引表示列号。通过这种方式,可以方便地访问和操作二维数组中的元素。
2.二维数组和一维数组的区别
1.维度差异:一维数组只有一个维度,而二维数组有两个维度,即行和列。
2.声明和访问方式不同:一维数组的声明和访问方式比较简单,可以直接通过数组名加索引的方式进行操作;而二维数组的声明和访问方式需要指定两个索引,即行和列。
3.存储方式不同:一维数组在内存中是连续存储的,每个元素之间没有额外的空间;而二维数组是一维数组的数组,每个一维数组在内存中也是连续存储的。
4.内存占用差异:由于二维数组包含多个一维数组,因此它的内存占用量通常要大于一维数组。
5.灵活性差异:一维数组的长度是固定的,并且元素的个数必须在声明时指定;而二维数组的长度可以在声明后进行动态调整,并且每个一维数组的长度可以不同。
总之,一维数组和二维数组在维度、声明和访问方式、存储方式、内存占用和灵活性等方面都存在差异。选择使用哪种数据结构应根据具体的需求和情况来决定。

大家看到了么,他们一个是线,一个是面。
3.二维数组的特点
二维数组是由多个一维数组组成的数据结构,它的特点如下:
1. 维度:二维数组有两个维度,通常用行和列表示。每个维度都可以有不同的长度。
2. 存储方式:二维数组在内存中是连续存储的,每个一维数组在内存中也是连续存储的。这意味着二维数组的元素在内存中是按照一定的顺序排列的。
3. 元素访问:二维数组的元素可以通过行和列的索引进行访问。通过指定行和列的索引,可以准确地找到特定的元素。
4. 元素类型:二维数组的元素可以是任意类型的数据,例如整数、浮点数、字符等。
5. 多维数组:二维数组是多维数组的一种特殊情况。除了二维数组之外,还可以有三维数组、四维数组等。多维数组可以理解为一维数组的数组。
6. 灵活性:二维数组的大小可以在声明后进行动态调整。每个一维数组的长度也可以不同,使得二维数组可以灵活地存储不同大小的数据。
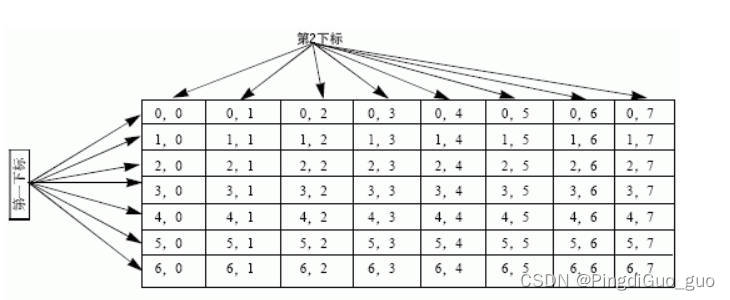
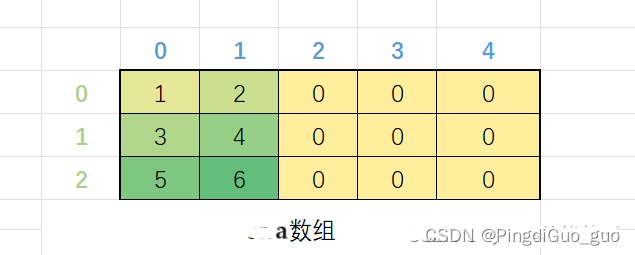
需要注意的是,二维数组不同于矩阵,矩阵是一个数学概念,有严格的数学定义和运算规则。而二维数组只是在内存中按照一定方式存储的数据结构,没有矩阵的特定性质和运算规则,并且二维数组与一维数组的下标特点一样,都是从零开始的。
附一张六行八列的下标
明式图:
4.二维数组的操作
1.定义
定义二维数组的代码如下:
// 行 列
int a[10][10];注意:我们在定义时,要用两个[ ]括号,他们分别表示的是行和列,数组类型可以是其他类型。

因为二维数组有两个维度,所以要有两个[ ]括号。
2.初始化
二维数组的初始化有两种方式:
1.直接赋值
直接赋值就是直接在代码里面赋值:
int arr[3][4];//三行四列
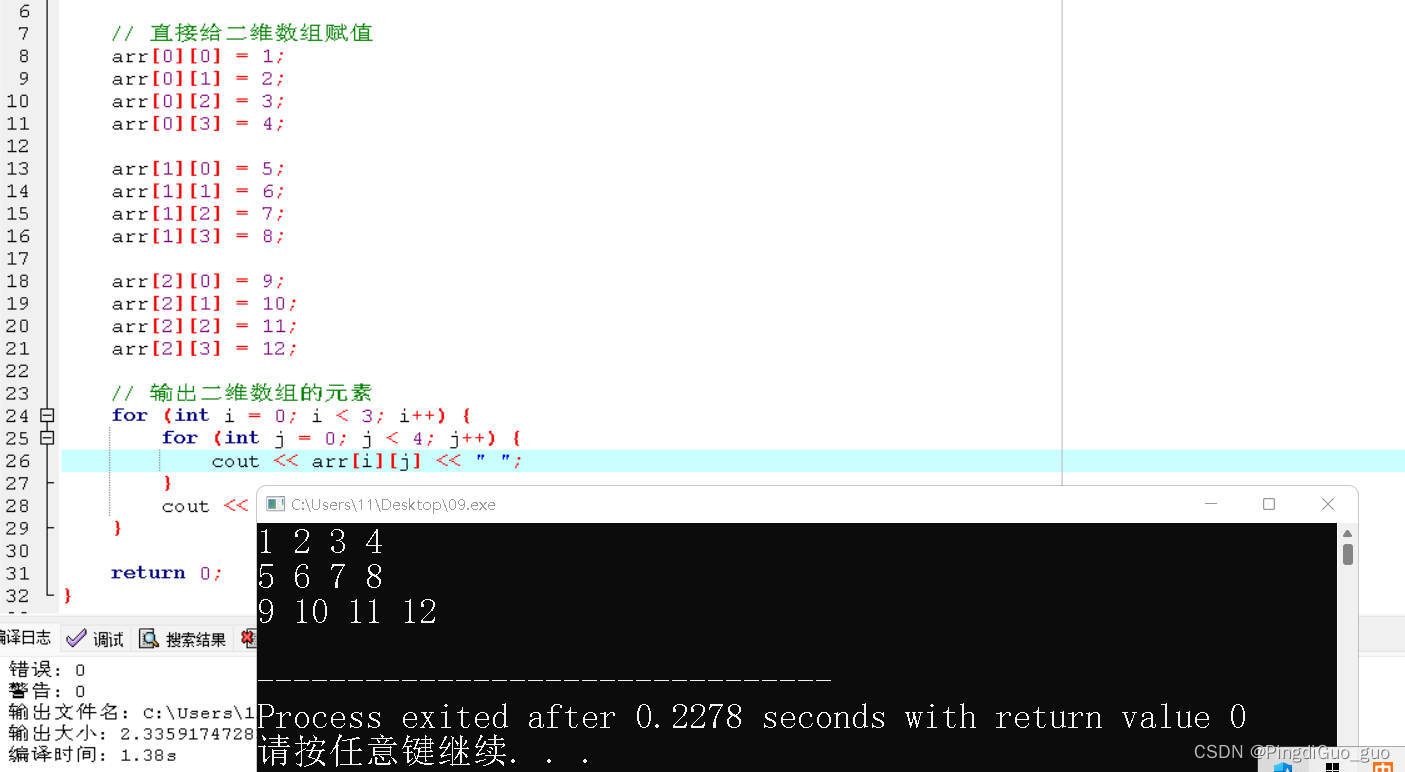
// 直接给二维数组赋值
arr[0][0] = 1;
arr[0][1] = 2;
arr[0][2] = 3;
arr[0][3] = 4;
arr[1][0] = 5;
arr[1][1] = 6;
arr[1][2] = 7;
arr[1][3] = 8;
arr[2][0] = 9;
arr[2][1] = 10;
arr[2][2] = 11;
arr[2][3] = 12;输出结果:
当然,还有另一种初始化:
int arr[3][4] = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12} };2.动态赋值
动态赋值就是输入赋值,因为他有两个维度,所以要用双重循环来解决输入问题,不了解双重循环的铁汁们可以看一下C++循环:简化重复的代码。我们可以用外层循环输入行,内层循环输入列。
代码如下:
// 定义一个3行4列的二维数组
int arr[3][4];
// 输入二维数组的元素
for (int i = 0; i < 3; i++) //行{
for (int j = 0; j < 4; j++)//列 {
cin >> arr[i][j];
}
}输出结果:

3.输出
输出也有两种方式:
1.直接输出
直接输出就是不用循环输出,如下:
cout<<a[0][0]<<' '<<a[0][1]<<' '<<a[0][2]<<a[0][3]<<endl;
cout<<a[1][0]<<' '<<a[1][1]<<' '<<a[1][2]<<a[1][3]<<endl;
cout<<a[2][0]<<' '<<a[2][1]<<' '<<a[2][2]<<a[2][3]<<endl;
2.动态输出
动态输出就是循环输出,与动态输入相似,代码如下:
// 循环输出二维数组的元素
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
std::cout << arr[i][j] << " ";
}
cout << std::endl;
}4.遍历
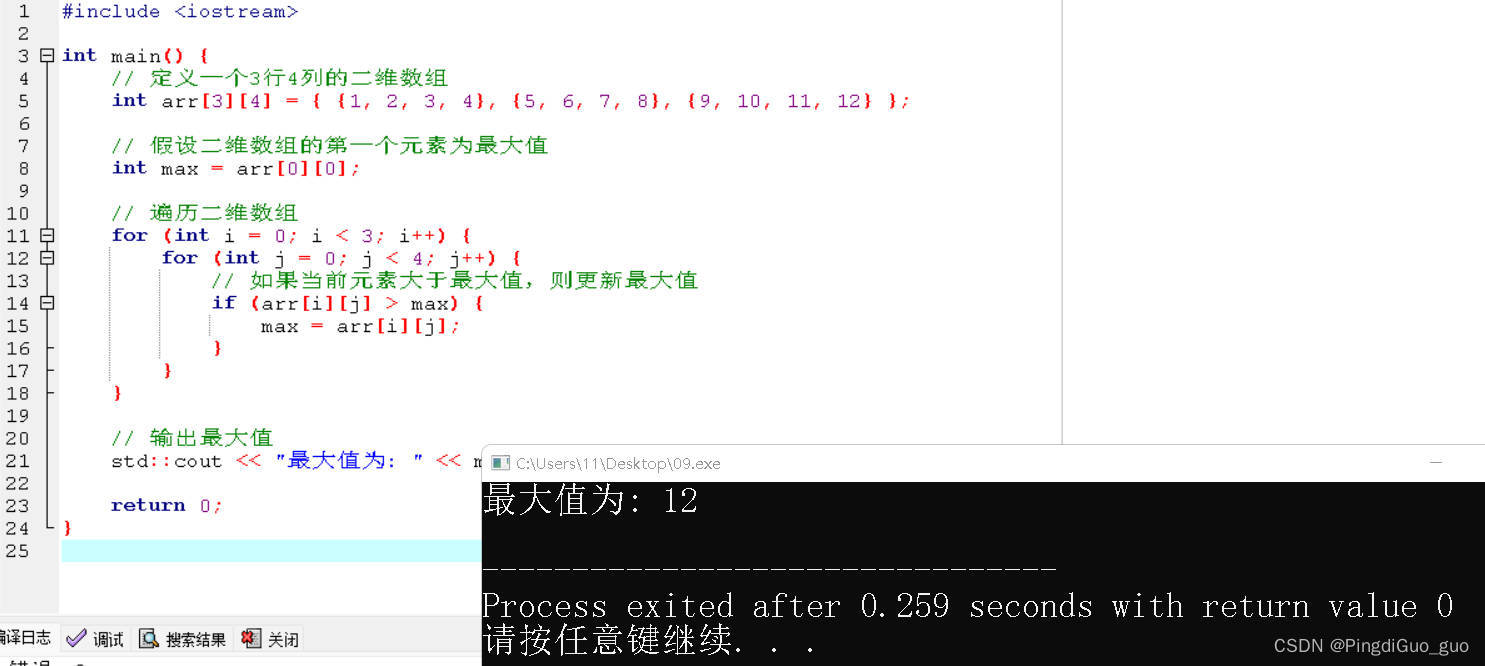
二维数组的遍历也需要双重循环,举一个求最大值的例子:
#include <iostream>
int main() {
// 定义一个3行4列的二维数组
int arr[3][4] = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12} };
// 假设二维数组的第一个元素为最大值
int max = arr[0][0];
// 遍历二维数组
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
// 如果当前元素大于最大值,则更新最大值
if (arr[i][j] > max) {
max = arr[i][j];
}
}
}
// 输出最大值
std::cout << "最大值为: " << max << std::endl;
return 0;
}
上述代码中,在遍历二维数组时,加入了一个判断语句,判断当前元素是否大于最大值。如果是,则更新最大值。最终输出的最大值即为遍历完成后的最大值。
输出结果:
5.排序
在C++中,有多种方法可以对二维数组进行排序。下面列举两种常用的方法:使用STL库函数和手动编写排序算法。
1.使用STL库函数
步骤:
1. 包含<algorithm>头文件。
2. 定义一个自定义的比较函数(用于指定排序的方式)。
3. 调用STL库函数std::sort进行排序。
#include <iostream>
#include <algorithm>
bool compare(const int* a, const int* b) {
return (*a < *b);
}
int main() {
// 定义一个3行4列的二维数组
int arr[3][4] = { {4, 2, 3, 1}, {8, 6, 7, 5}, {12, 10, 11, 9} };
// 定义一个一维数组,用于存放二维数组的元素
int* arr1d[3];
for (int i = 0; i < 3; i++) {
arr1d[i] = arr[i];
}
// 对一维数组进行排序
std::sort(arr1d, arr1d + 3, compare);
// 输出排序后的二维数组
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
std::cout << arr1d[i][j] << " ";
}
std::cout << std::endl;
}
return 0;
}
2.手写排序算法
步骤:
1. 可以使用冒泡排序、选择排序、插入排序等常见排序算法进行排序。
2. 在排序过程中,比较两个元素进行交换,直到所有元素都按照特定顺序排列。
#include <iostream>
void bubbleSort(int arr[][4], int rows) {
for (int i = 0; i < rows; i++) {
for (int j = 0; j < 4 - 1; j++) {
for (int k = 0; k < 4 - j - 1; k++) {
if (arr[i][k] > arr[i][k + 1]) {
int temp = arr[i][k];
arr[i][k] = arr[i][k + 1];
arr[i][k + 1] = temp;
}
}
}
}
}
int main() {
// 定义一个3行4列的二维数组
int arr[3][4] = { {4, 2, 3, 1}, {8, 6, 7, 5}, {12, 10, 11, 9} };
// 对二维数组进行排序
bubbleSort(arr, 3);
// 输出排序后的二维数组
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
std::cout << arr[i][j] << " ";
}
std::cout << std::endl;
}
return 0;
}
6.插入
1.在头部插入
步骤:
1. 将原数组中的元素向后移动一行。
2. 将要插入的元素放入第一行。
#include <iostream>
int main() {
// 原二维数组(大小为4x4)
int arr[4][4] = { {4, 2, 3, 1}, {8, 6, 7, 5}, {12, 10, 11, 9} };
// 插入元素到头部
int newRow[4] = {11, 12, 13, 14};
for (int i = 3; i > 0; i--) {
for (int j = 0; j < 4; j++) {
arr[i][j] = arr[i - 1][j];
}
}
for (int j = 0; j < 4; j++) {
arr[0][j] = newRow[j];
}
// 输出新数组
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
std::cout << arr[i][j] << " ";
}
std::cout << std::endl;
}
return 0;
}
2.在中间插入
步骤:
1. 将原数组中的元素向后移动一行,从要插入的行开始。
2. 将要插入的元素放入指定行。
#include <iostream>
int main() {
// 原二维数组(大小为4x4)
int arr[4][4] = { {4, 2, 3, 1}, {8, 6, 7, 5}, {12, 10, 11, 9} };
// 插入元素到中间
int rowIndex = 1; // 要插入的行号
int newRow[4] = {11, 12, 13, 14};
for (int i = 3; i > rowIndex; i--) {
for (int j = 0; j < 4; j++) {
arr[i][j] = arr[i - 1][j];
}
}
for (int j = 0; j < 4; j++) {
arr[rowIndex][j] = newRow[j];
}
// 输出新数组
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
std::cout << arr[i][j] << " ";
}
std::cout << std::endl;
}
return 0;
}3.在尾部插入
步骤:
1. 将要插入的元素放入最后一行。
#include <iostream>
int main() {
// 原二维数组(大小为4x4)
int arr[4][4] = { {4, 2, 3, 1}, {8, 6, 7, 5}, {12, 10, 11, 9} };
// 插入元素到尾部
int newRow[4] = {11, 12, 13, 14};
for (int j = 0; j < 4; j++) {
arr[3][j] = newRow[j];
}
// 输出新数组
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
std::cout << arr[i][j] << " ";
}
std::cout << std::endl;
}
return 0;
}5.练习
题目:给定一个二维矩阵,将矩阵顺时针旋转90度。
初始思路:
可以先创建一个和原矩阵大小相同的新矩阵,然后将原矩阵中每个元素按照旋转的规则放入新矩阵的对应位置。
代码:
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> rotateMatrix(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> rotated(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
rotated[j][m - i - 1] = matrix[i][j];
}
}
return rotated;
}
void printMatrix(const vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cout << matrix[i][j] << " ";
}
cout << endl;
}
}
int main() {
int m, n;
cin >> m >> n;
vector<vector<int>> matrix(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j];
}
}
vector<vector<int>> rotatedMatrix = rotateMatrix(matrix);
printMatrix(rotatedMatrix);
return 0;
}修改后的思路:
为了节省空间,可以直接在原矩阵上进行原地旋转。通过观察可以发现,将矩阵顺时针旋转90度等价于先进行转置操作,再将每一行逆序。
代码:
#include <iostream>
#include <vector>
using namespace std;
void rotateMatrix(vector<vector<int>>& matrix) {
int n = matrix.size();
// 转置矩阵
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
swap(matrix[i][j], matrix[j][i]);
}
}
// 每一行逆序
for (int i = 0; i < n; i++) {
reverse(matrix[i].begin(), matrix[i].end());
}
}
void printMatrix(const vector<vector<int>>& matrix) {
int n = matrix.size();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << matrix[i][j] << " ";
}
cout << endl;
}
}
int main() {
int n;
cin >> n;
vector<vector<int>> matrix(n, vector<int>(n, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j];
}
}
rotateMatrix(matrix);
printMatrix(matrix);
return 0;
}6.总结
本篇博客到这里就结束了,感谢大家的支持与观看,如果有好的建议欢迎留言,谢谢大家啦!








![[Linux] 网络编程套接字](https://img-blog.csdnimg.cn/direct/ef4e1404aad748e286d7b5c275aaaf85.png)