由数据范围反推算法复杂度以及算法内容 - AcWing
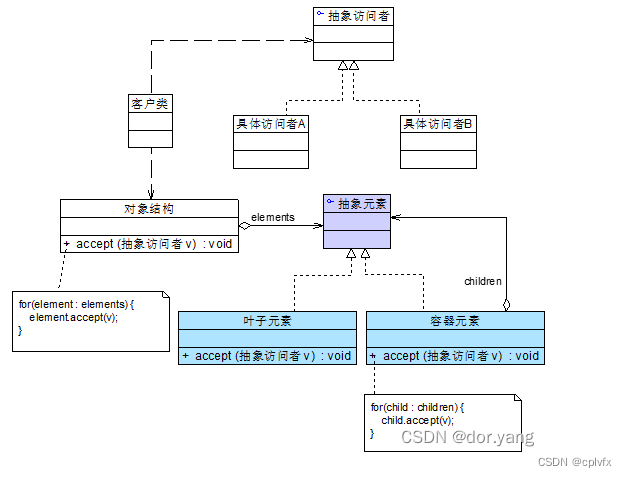
常用代码模板4——数学知识 - AcWing
基本思想:
首先,我们给出质数的定义,指在大于1的自然数中,除了1和该数自身外,无法被其他自然数整除的数。这里考虑三个问题:
(一)质数的判定—试除法
我们很容易想到用暴力来做,从2遍历到数n,代码如下:
bool isPrime(int n) { for(int i = 2; i <= n; i++) { if(n % i == 0) return false; } return true; }
可以看出时间复杂度为O(n),那么当我们判断m个数是否为质数时复杂度就变成了O(n * m),容易超时,这时候我们就要去考虑优化了,数论这块内容主要考察的是对数学知识的掌握,我们可以发现质数的因数是成对出现的,即d | n(d能整除n),那么(n/d) | n , (例如:12%3=0 12%(12/3) =0)

我们每次就只用枚举较小的那个因数即可,这样我们的时间复杂度就可以从O(n)降到O(sqrt(n))
866. 试除法判定质数 - AcWing题库
给定 n 个正整数 ai,判定每个数是否是质数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
共 n 行,其中第 i 行输出第 i 个正整数 ai 是否为质数,是则输出 Yes,否则输出 No。
数据范围
1≤n≤100,
1≤ai≤2^31−1
输入样例:
2
2
6
输出样例:
Yes
No#include<iostream> using namespace std; int n; bool is_prime(int x) { if(x < 2) return false; for(int i = 2; i <= x / i; i++) { if(x % i == 0) return false; //n/d n/n/d 12/3 12/12/3-> 12/4 质数的约数是成对出现的 变化一下就可以从O(n)优化到O(sqrt(n) } return true; } int main() { cin>>n; while(n--) { int x; cin >> x; if(is_prime(x)) cout << "Yes" << endl; else cout << "No" << endl; } return 0; }
(二)分解质因数——试除法
对于任何一个大于1的自然数 n,如果n不为质数,那么n可以唯一分解成有限个质数的乘积,即:

所以,我们可以扫描2~sqrt(N)之间的每一个整数i,若i能整除n,则从n中除掉所有的因子i,同时累计除去的i的个数,且当条件if(n % i == 0)成立时,i一定为n的一个质因子。这里我们的时间复杂度最坏情况为O^(sqrt(n)),而最好情况为O^(log(n)),比如当n为2的k次方时,一次就除尽了,一般情况下是优于试除法的效率。
867. 分解质因数 - AcWing题库
给定 n 个正整数 ai,将每个数分解质因数,并按照质因数从小到大的顺序输出每个质因数的底数和指数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
对于每个正整数 ai,按照从小到大的顺序输出其分解质因数后,每个质因数的底数和指数,每个底数和指数占一行。
每个正整数的质因数全部输出完毕后,输出一个空行。
数据范围
1≤n≤100,
2≤ai≤2×10^9
输入样例:
2
6
8
输出样例:
2 1
3 1
2 3
#include<iostream> using namespace std; int n; //时间复杂度最坏情况为O^(sqrt(n)),最好情况为O^(log(n)),比如当n为2的k次方时,一次就除尽了。 void divide(int n) { for(int i = 2; i <= n / i; i++) { if(n % i == 0) //满足这个条件那么i一定是质因子,将n看作几个质因数相乘 { int s = 0; while(n % i == 0) { n /= i; s++; } cout << i << " " << s << endl; } } if(n > 1) cout << n << " 1" << endl; //我们优化到只用循环sqrt(n)次,所以只用特判一下,如果n没有除尽说明还剩下一个大于sqrt(n)的质因子 //而且n肯定只包含一个大于sqrt(n)的质因子,因为如果有俩,他们的乘积就大于n了,这是不可能的 } int main() { cin>>n; while(n--) { int x; cin>>x; divide(x); puts(""); } return 0; }
(三)求质数个数(筛质数)——朴素筛法,埃及筛法和线性筛法
筛质数的核心思想就是,对于n个数,从2开始枚举,依次将其倍数删去,如果枚举到该数仍存在则该数一定为质数,因为例如一个数p,枚举到它时还存在,说明它不是2~p-1中任何数的倍数,即该数为质数。

所以,很容易得到我们的朴素筛法,即循环2~n每次删掉当前数的倍数,分析时间复杂度,循环n-1次,每次循环n/i次,即n/2+n/3+.....+n/n -> n(ln n + c),即时间复杂度可看作(nlogn)
void get_primes(int n) { for (int i = 2; i <= n; i++) { if (st[i]) continue; primes[cnt++] = i; for (int j = i + i; j <= n; j += i) st[j] = true; } }
埃及筛法就是在朴素筛法的基础上,我们只用将质数的倍数删掉即可,因为一个合数可以写成几个质数的积,那么我们将所有质数的倍数删掉时,所有合数也被删掉了,这样可以将时间复杂度优化到O(nloglogn),可粗略看作O(n)。
void get_primes(int n) { for (int i = 2; i <= n; i++) { if (!st[i]) { primes[cnt++] = i; for (int j = i + i; j <= n; j += i) st[j] = true; } } }
线性筛法,核心是每一个数n只会被它的最小质因子筛掉,我们扫描2~n,如果当前数没有被删掉,那么它就是质数,我们将其添加到质数数组里,在每次循环中,我们从小到大枚举每一个质数,当 i%pj == 0, pj定为i最小质因子,pj也定为pj*i最小质因子 ,当i%pj != 0, pj定小于i的所有质因子,所以pj也为pj*i最小质因子,这样我们就可以将以pj作为最小质因子的合数删去。对于任意一个合数x,假设pj为x的最小质因子,当i枚举到x / pj 时,我们就会将x删去,保证了每个数都会被遍历到,且if(i % primes[j] == 0) break;保证了在走完当前所有质数之前,一定会遇到i%primes[j]==0.所以不需要加判断j <= cnt的条件。

void get_primes(int n) { for (int i = 2; i <= n; i++) { if (!st[i]) primes[cnt++] = i; for (int j = 0; primes[j] <= n / i; j++) { st[primes[j] * i] = true; if (i % primes[j] == 0) break; } } }
868. 筛质数 - AcWing题库
给定一个正整数 n,请你求出 1∼n 中质数的个数。
输入格式
共一行,包含整数 n。
输出格式
共一行,包含一个整数,表示 1∼n 中质数的个数。
数据范围
1≤n≤10^6
输入样例:
8
输出样例:
4//朴素筛法 /*#include<iostream> #include<algorithm> using namespace std; const int N = 1000010; int primes[N],cnt; bool st[N]; int n; void get_primes(int n) { for(int i = 2; i <= n; i++) { if(!st[i]) primes[cnt++] = i; for(int j = i + i; j <= n; j += i) st[j] = true; } } int main() { cin>>n; get_primes(n); cout << cnt; return 0; } */ //埃及筛法 /*#include<iostream> #include<algorithm> using namespace std; const int N = 1000010; int primes[N],cnt; bool st[N]; int n; void get_primes(int n) { for(int i = 2; i <= n; i++) { if(!st[i]) { primes[cnt++] = i; for(int j = i + i; j <= n; j += i) st[j] = true; } } } int main() { cin>>n; get_primes(n); cout << cnt; return 0; } */ //线性筛法 #include<iostream> #include<algorithm> using namespace std; const int N = 1000010; int primes[N],cnt; bool st[N]; int n; void get_primes(int n) { for(int i = 2; i <= n; i++) { if(!st[i]) primes[cnt++] = i; for(int j = 0; primes[j] <= n / i; j++) { st[primes[j] * i] = true; if(i % primes[j] == 0) break; } } } int main() { cin>>n; get_primes(n); cout << cnt; return 0; }