时间序列预测—

时间序列预测——GRU模型

news2025/1/18 7:33:05

时间序列预测——GRU模型

在深度学习领域，循环神经网络（RNN）是处理时间序列数据的一种常见选择。上期已介绍了LSTM的单步和多步预测。本文将深入介绍一种LSTM变体——门控循环单元（GRU）模型，包括其理论基础、公式、优缺点，并通过Python实现单步预测的示例。同时，将与长短时记忆网络（LSTM）进行比较，以更好地理解GRU的特性。

1. 引言

循环神经网络（RNN）是一类专门用于处理序列数据的神经网络。然而，传统的RNN存在梯度消失和梯度爆炸等问题，这导致了对长序列的有效建模变得困难。为了解决这些问题，门控循环单元（GRU）被提出。

2. GRU模型的理论

2.1 简介

GRU cell

门控循环单元（GRU）是由Cho等人于2014年提出的，旨在解决长短时记忆网络（LSTM）的一些问题。与LSTM相似，GRU也具有长期依赖性建模的能力，但其结构更加简单。GRU通过更新门和重置门来控制信息的流动，减少了参数数量，使得训练更加高效。

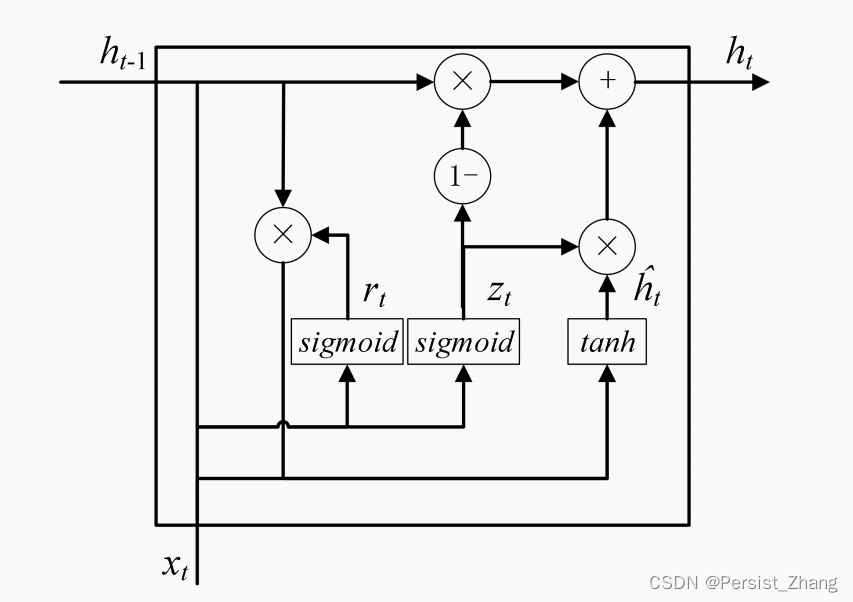
2.2 GRU的结构

GRU由两个门控制：更新门（Update Gate）和重置门（Reset Gate）。与LSTM不同，GRU没有细胞状态，而是直接使用隐藏状态。

GRU的隐藏状态更新公式为：

$\begin{equation} h_t = (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t \end{equation}$

其中：

$h_t$ 是当前时间步的隐藏状态。
$z_t$ 是更新门的输出。
$\odot$ 是逐元素相乘操作。
$\tilde{h}_t$ 是当前时间步的候选隐藏状态。

2.3 更新门和重置门

更新门（Update Gate）和重置门（Reset Gate）的计算分别为：

$\begin{equation} z_t = \sigma(W_z \cdot [h_{t-1}, x_t]) \end{equation}$

$\begin{equation} r_t = \sigma(W_r \cdot [h_{t-1}, x_t]) \end{equation}$
其中：

$W_z$ 和 $W_r$ 是权重矩阵。
$\sigma$ 是sigmoid激活函数。
$h_{t-1}, x_t]$ 是当前时间步的隐藏状态和输入拼接而成的向量。

2.4 候选隐藏状态

候选隐藏状态（Candidate Hidden State）的计算为：

$\begin{equation} \tilde{h}_t = \tanh(W \cdot [r_t \odot h_{t-1}, x_t]) \end{equation}$

其中：

$W$ 是权重矩阵。

3. GRU模型与LSTM的区别

GRU与LSTM有相似之处，都采用了门控制机制，但它们在结构上存在一些区别。

参数数量：GRU的参数数量相对较少，因为它没有细胞状态，直接使用隐藏状态。
计算效率：由于参数较少，GRU在训练和预测时通常更加高效。
表达能力：LSTM的细胞状态允许更好地保留和传递信息，适用于更复杂的序列建模任务。但在某些场景下，GRU由于其简单性能够表达一些简单序列的依赖关系。

4. Python实现GRU的单步预测

接下来，将使用Python和深度学习库Keras实现GRU的单步预测。将使用一个简单的时间序列数据集，以便清晰展示模型的训练和预测过程。

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import GRU, Dense

# 创建示例时间序列数据
np.random.seed(42)
data = np.arange(0, 100, 0.1)
noise = np.random.normal(0, 1, len(data))
data += noise

# 准备训练数据
seq_length = 10
x, y = [], []

for i in range(len(data) - seq_length):
    x.append(data[i:i + seq_length])
    y.append(data[i + seq_length])

x = np.array(x)
y = np.array(y)

x = x.reshape((x.shape[0], x.shape[1], 1))

# 构建GRU模型
model = Sequential()
model.add(GRU(50, activation='relu', input_shape=(seq_length, 1)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')

# 训练GRU模型
model.fit(x, y, epochs=50, verbose=0)

# 使用训练好的模型进行单步预测
input_data = data[-seq_length:].reshape((1, seq_length, 1))
predicted_value = model.predict(input_data, verbose=0)

# 可视化结果
plt.figure(figsize=(12, 6))
plt.plot(data, label='Original Data')
plt.scatter(len(data) - 1, predicted_value, color='red', marker='o', label='GRU Prediction (Single Step)')
plt.title('GRU Model - Single Step Prediction')
plt.legend()
plt.show()