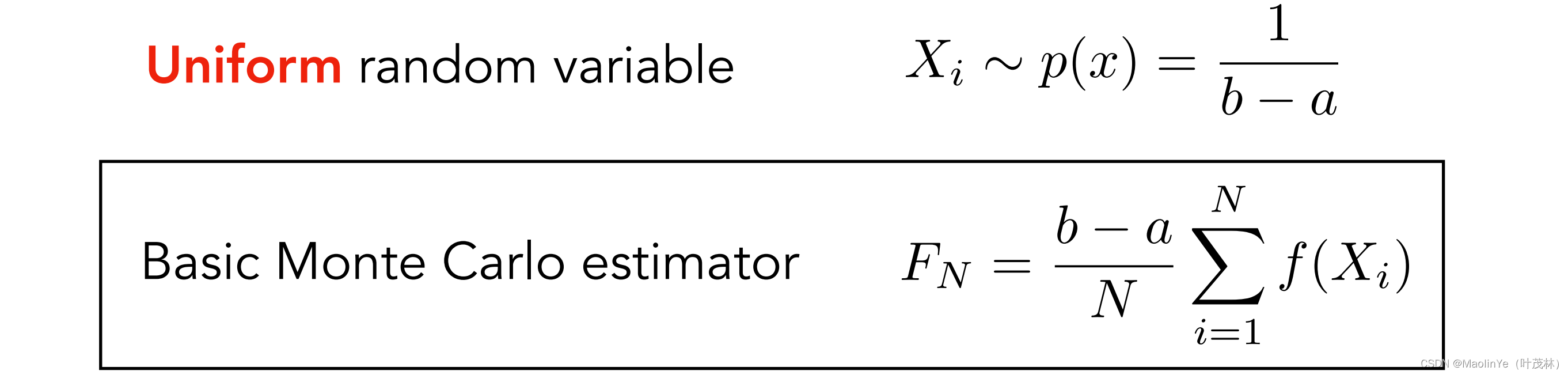为了后面要讲的路径追踪，需要讲一下这个蒙特卡洛积分，同时需要回顾一下高等数学中的微积分和概率论与统计学的知识
目录
微积分
概念论与统计
蒙特卡洛积分
微积分
定积分是微积分中的一种重要概念，用于计算函数在一个区间上的总体积、总面积或总量，对于一个实函数 f(x)，定积分可以表示为∫[a, b] f(x) dx，其中 [a, b] 是积分区间，f(x) 是被积函数，dx 表示与自变量 x 相关的微小增量
不定积分是微积分中的一种概念，用于求解函数的原函数（或称为反导函数），可以理解为找到一个函数 F(x)，使得 F'(x) = f(x)，其中 F'(x) 表示函数 F(x) 的导数，这个函数 F(x) 就是函数 f(x) 的不定积分
不定积分可以用来求解定积分的值：如果在一个区间上求出了函数 f(x) 的一个原函数 F(x)，那么在该区间上的定积分 ∫[a, b] f(x) dx 就等于 F(b) - F(a)
概念论与统计
对于一个连续的随机变量X，它的取某个值的概率由概率分布函数给出，也就是PDF
根据概率的特性，概率p是非负的，而且PDF的积分等于1，该随机变量的数学期望可以通过xp(x)dx的积分得到
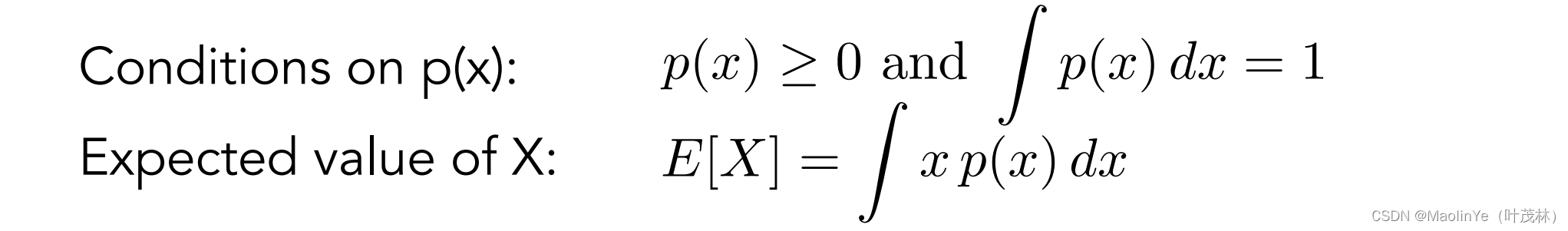
如果Y = f(X)，那么Y的数学期望可以这样算
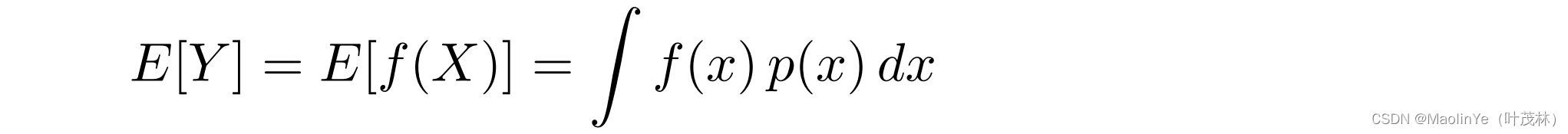
蒙特卡洛积分
上面说过，定积分可以用来计算函数在某个区间的面积，可以通过函数的不定积分来计算，但是如果这个函数的不定积分的式子很难找到或者无法表示呢，那通过不定积分来计算定积分就比较困难
定积分本质思想是无穷累加，把区间[a,b]之间的宽为dx高为f(x)的长方形面积都加起来作为定积分的结果，而蒙特卡洛积分则是通过随机采样x，以f(x)为高、区间长度为宽计算面积，并通过多次采样取平均面积作为积分的结果
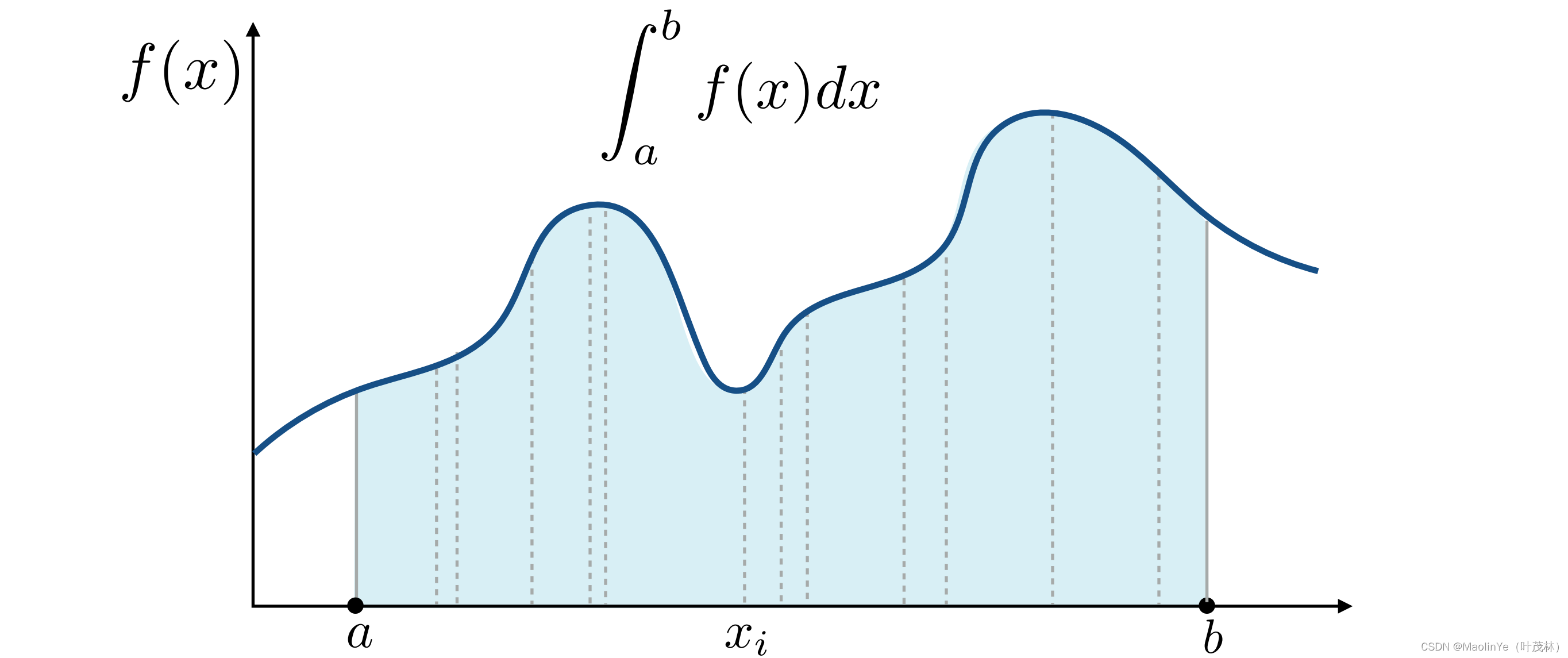
具体来说，从数学上定义蒙特卡洛积分，它的值就是随机采样x的函数值f(x)除以采样的概率p(x)再累加求平均
举个例子，假设采样是均匀采样，那么采样的概率都是1/(b-a)
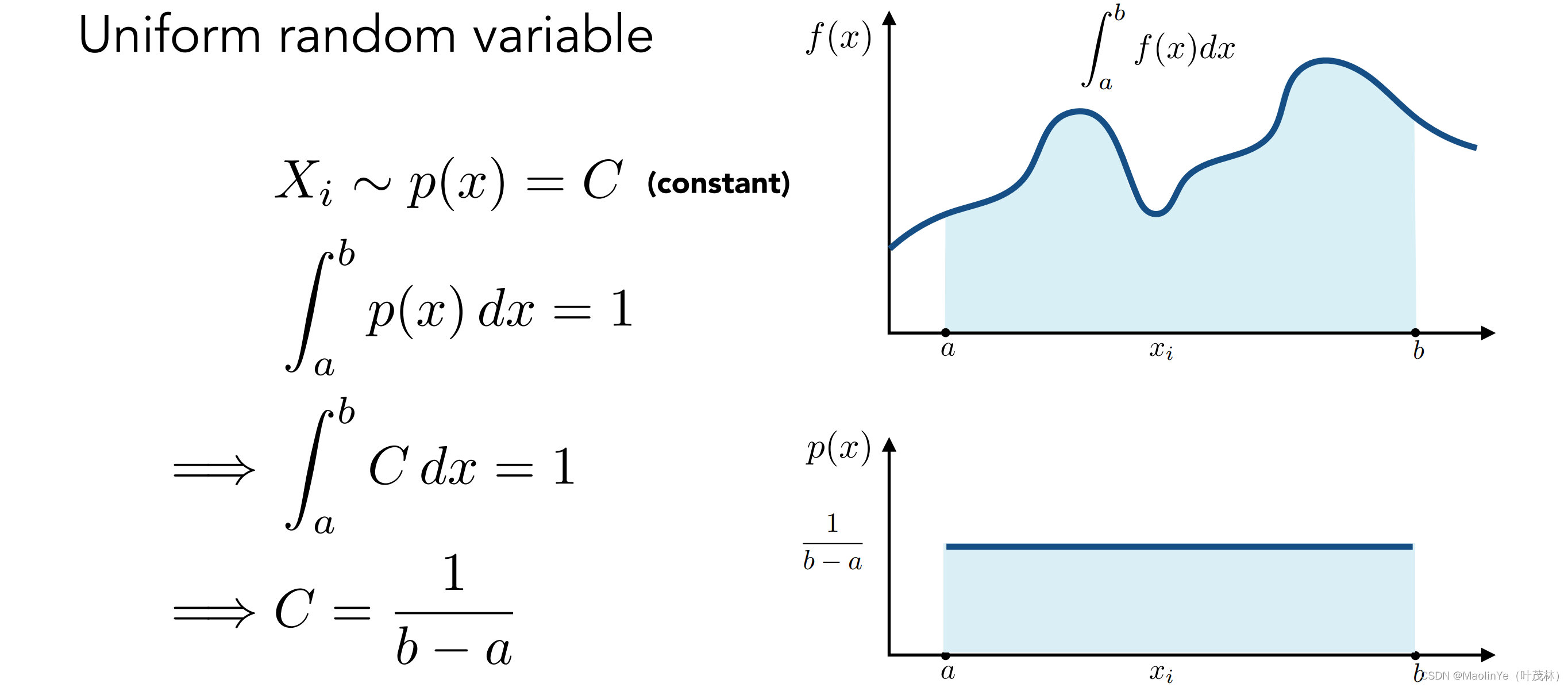
那么蒙特卡洛积分的结果就是下面这个式子
