869. 试除法求约数

思路：

约数和质数的求解有着共性， 就是都是使用

for (int i = 1; i <= n/i; ++i)

进行计算的。这样的原因是因为约数必然也是两两一组， 那么我们求出小的自然也就知道另一个，只要再判断一下n/i和i是否相同，就行了。但是由于设计到输出的时候的排序问题，所以我们使用sort函数进行排序。最后输出。

代码：

#include <iostream>

using namespace std;

// 暴力解法， 会超时
/*
int main ()
{
    int n, a;
    scanf ("%d", &n);

    while (n--)
    {
        scanf ("%d", &a);
        for (int i = 1; i <= a; ++i)
            if (a%i == 0) printf ("%d ", i);
        printf ("\n");
    }
}
*/

#include <algorithm>
#include <vector>

vector<int> get_divisors (int n)
{
    vector<int> res;

    for (int i = 1; i <= n/i; i++)
    {
        if (n%i == 0)
        {
            res.push_back (i);
            if (i != n/i) res.push_back (n/i);
        }
    }

    sort (res.begin (), res.end ());

    return res;
}

int main ()
{
    int a, n;
    scanf ("%d", &a);

    while (a--)
    {
        scanf ("%d", &n);
        auto res = get_divisors (n);

        for (auto t : res) printf ("%d ", t);
        printf ("\n");
    }
}

我不会的地方再说一遍：

vector容器输入是push_back(), 头是begin(), 尾的下一个是end(), 这几个都是指针。

870. 约数个数

思路：

约数的个数公式将n分解成质因子

也就是说，多个数的乘积的约数，我们可以通过分别求数的质因子及指数·， 通过unordered_map容器统计出质因子分别的个数，其实我们也就知道了乘积的质因子个数。

代码：

#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;
typedef long long LL;
const int mod = 1e9+7;

int main ()
{
    int n;
    scanf ("%d", &n);
    unordered_map<int, int> primes;

    while (n--)
    {
        int a;
        scanf ("%d", &a);

        for (int i = 2; i <= a/i; i++)
            while (a%i == 0)
        {
            a /= i;
            primes[i] ++;
        }

        if (a > 1) primes[a] ++;
    }

    LL res = 1;
    for (auto prime : primes) res = res*(prime.second+1)%mod;

    cout << res << endl;

    for (auto prime : primes) cout << prime.first << " " << prime.second << endl;
}

871. 约数之和

思路：

n个数乘积的约数和和约数个数的求法有相同之处。

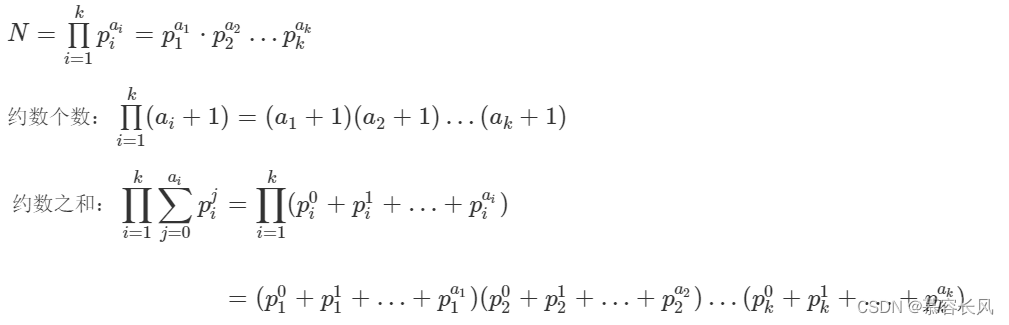
找了一个公式，p1、p2分别表示底数， a1、a2分别表示指数。也就是咱们前面求出质因子及对应的指数之后我们分别求出质因子的0到指数（设为a）的和并相乘。

代码：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <math.h>

using namespace std;

const int mod = 1e9+7;

typedef long long LL;

int main ()
{
    int n;
    cin >> n;
    unordered_map<int, int> primes;

    while (n--)
    {
        int a;
        cin >> a;

        for (int i = 2; i <= a/i; ++i)
        {
            while (a%i == 0)
            {
                a /= i;
                primes[i] ++;
            }
        }

        if (a > 1) primes[a]++;
    }

    LL res = 1;
    for (auto prime : primes)
    {
        int p = prime.first, a = prime.second;
        LL t = 1;
        while (a--) t = (t*p + 1) % mod;
        res = res * t % mod;

        cout << prime.first << " " << prime.second << " " << t << " " << res << endl;
    }
    cout << res << endl;
}

这里的这一行while (a--) t = (t*p + 1) % mod;质因子从指数为0相加到指数为a。

872. 最大公约数

代码：

#include <iostream>

using namespace std;

int gcd (int a, int b)
{
    if (b == 0)
        return a;

    return gcd(b, a % b);
}

int main ()
{
    int n;
    cin >> n;

    while (n--)
    {
        int a, b;
        cin >> a >> b;
        cout << gcd(a, b) << endl;
    }
}