创作不易,友友们给个三连吧!!
一、旋转数组(力扣)
经典算法OJ题:旋转数组
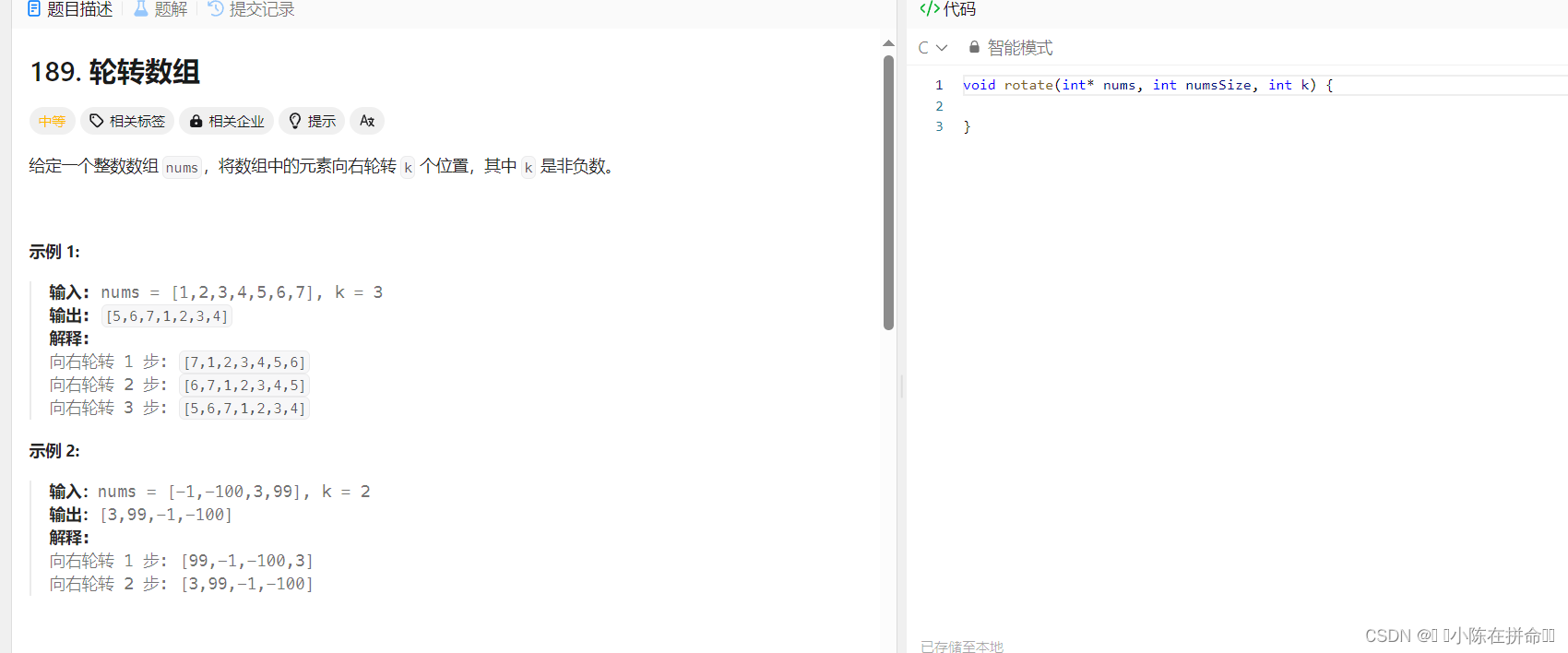
思路1:每次挪动1位,右旋k次
时间复杂度:o(N^2)
右旋最好情况:k是n的倍数,相当于不右旋,此时为o(1)
右旋最坏情况:k%n==n-1,此时为o(N^2)
空间复杂度:o(1)
void rotate(int* nums, int numsSize, int k)
{
k%=numsSize;
while(k)
{
int temp=nums[numsSize-1];
//从后往前挪
for(int i=numsSize-1;i>0;i--)
{
nums[i]=nums[i-1];//最后一个是nums[1]=num[0]
}
nums[0]=temp;
k--;//旋转一次就减一次
}
}注:这是常规思路,但是由于空间复杂度太高,数组个数特别多的时候,在力扣运行的时候超出了时间限制!

思路2:创建一个和nums一样长度的新数组,将nums数组的后k个元素,先按顺序放进新数组里,然后剩下前面的n-k个元素,再按顺序放进新数组,最后再将新数组的数据拷贝到nums中
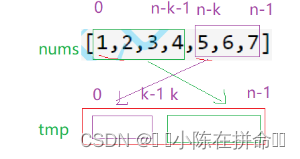
时间复杂度:o(N)
空间复杂度:o(N)
void rotate(int* nums, int numsSize, int k)
{
k%=numsSize;
int arr[numsSize];//vs不支持变长数组,但是牛客支持,如果是vs只能使用动态数组。
memcpy(arr,nums+numsSize-k,sizeof(int)*k);//nums的后k个按顺序拷贝到新数组的前面
memcpy(arr+k,nums,sizeof(int)*(numsSize-k));//nums的前n-k个按顺序拷贝到新数组的后面
memcpy(nums,arr,sizeof(int)*numsSize);//新数组完全拷贝到nums数组中
}思路3:前n-k个元素逆置,后k个元素逆置,再整体逆置

时间复杂度:o(N)
空间复杂度:o(1)
void reverse (int *arr,int left,int right)//实现逆序函数
{
int temp=0;
while(left<right)
{
temp=arr[left];
arr[left]=arr[right];
arr[right]=temp;
left++;
right--;
}
}
void rotate(int* nums, int numsSize, int k)
{
k%=numsSize;
reverse(nums,0,numsSize-k-1);//前n-k个元素逆序
reverse(nums,numsSize-k,numsSize-1);//后k个逆序
reverse(nums,0,numsSize-1);//完全逆序
}二、消失的数字(力扣)
经典算法OJ题:消失的数字

思路1:先进行排序,如果后一个不等于前一个+1,就可以找到消失的数据,但是目前掌握的排序中,冒泡排序的时间复杂度是o(N^2),而qsort的时间复杂度是o(logN+N),均不符合题意,这里不做考虑!
思路2:让0和0-numsSize的所有数都异或一遍,再和数组中的所有元素异或一边,最后得到的结果就是消失的数(利用了a^a=0,a^0=a的结论)
时间复杂度:o(N)
空间复杂度:o(1)
int missingNumber(int* nums, int numsSize)
{
int x=0;
for(int i=0;i<numsSize;i++)
{
x^=i;
x^=nums[i];
}
x^=numsSize;//还多了一个数
return x;
}思路3:0-numsSize的所有数相加,然后减去数组中的所有元素之和,得到的就是消失的数字。
时间复杂度:o(N)
空间复杂度:o(1)
int missingNumber(int* nums, int numsSize)
{
int sum=0;//记录
for(int i=0;i<numsSize;i++)
{
sum+=i;
sum-=nums[i];
}
sum+=numsSize;
return sum;
}
三、链表中倒数第k个结点(牛客)
经典算法OJ题:链表中倒数第k个结点

思路1:第一次循环计算结点的个数count,然后求倒数第k个就是正数的第count-k个结点
空间复杂度:o(N)
时间复杂度:o(1)
typedef struct ListNode ListNode;
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k )
{
ListNode* pcur= pListHead;
int count=0;//统计结点
while(pcur)
{
pcur=pcur->next;
count++;
}
if(count<k)
return NULL;//考虑链表为NULL,以及k大于链表结点数
pcur= pListHead;
for(int i=0;i<count-k;i++)
pcur=pcur->next;
return pcur;
}思路2:(快慢指针)fast指针先走k步,然后fast和slow同时走,始终保持k的距离,当fast走到NULL的时候,slow对应的恰好就是倒数第k个结点
空间复杂度:o(N)
时间复杂度:o(1)
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k )
{
struct ListNode*fast=pListHead,*slow=pListHead;
while(k)
{
//考虑k大于结点数的情况,此时链表很早就为空了
if(fast==NULL)
return NULL;
fast=fast->next;
k--;
}
//同时走,直到fast为NULL,此时slow指向倒数第k个结点
while(fast)
{
fast=fast->next;
slow=slow->next;
}
//如果k<=0.那么第一个while循环不会进入,
//fast和slow同时走,最后都会指向空,所以不需要额外判断
return slow;
}思路3:直接反转链表,然后直接找第k个结点
该方法直接改变了链表结构,使得phead变成了一个尾结点,与其他结点建立不起联系,所以该思路不行(尽量不要去改变原先链表的结构)在力扣中过不了。
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k )
{
//直接反转链表,然后找第k个结点
if(pListHead==NULL)
return NULL;
struct ListNode*p1=NULL;
struct ListNode*p2=pListHead;
struct ListNode*p3=pListHead->next;
int count=0;//用来数数
while(p2)
{
p2->next=p1;
p1=p2;
p2=p3;
if(p3)
p3=p3->next;
++count;
}
//此时的p1就是新链表的头结点
if(k<=count||k>count)
return NULL;
while(--k)
{
p1=p1->next;
}
return p1;
}
四、相交链表(力扣)
经典算法OJ题:相交链表

思路1:A链表逐个结点与B链表比较,如果存在相等,则就是相交结点(注:要比较指针而不能比较值,因为值是可以重复的)
空间复杂度:o(N^2)
时间复杂度:o(1)
typedef struct ListNode ListNode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
ListNode* pcurA=headA;
ListNode* pcurB=headB;
while(pcurA)
{
while(pcurB)
{
if(pcurA==pcurB)
return pcurA;
pcurB=pcurB->next;
}
pcurB=headB;
pcurA=pcurA->next;
}
return NULL;
}思路2:长的链表往后走长度差,再同时走,直到相等就是相交点
空间复杂度:o(N)
时间复杂度:o(1)
typedef struct ListNode ListNode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
ListNode * Apcur=headA;//用来遍历A链表
ListNode * Bpcur=headB;//用来遍历A链表
int a=0;//数a长度
int b=0;//数b长度
while(Apcur)
{
Apcur=Apcur->next;
a++;
}
while(Bpcur)
{
Bpcur=Bpcur->next;
b++;
}
//找最小数,写俩while循环,只要大的数才可以走,小的走不了
int m=a>b?b:a;
while(a-m)
{
headA=headA->next;
a--;
}
while(b-m)
{
headB=headB->next;
b--;
}
while(headA)
{
if(headA==headB)
return headA;
headA=headA->next;
headB=headB->next;
}
return NULL;
}五、链表的回文结构(牛客)
经典算法OJ题:链表的回文结构
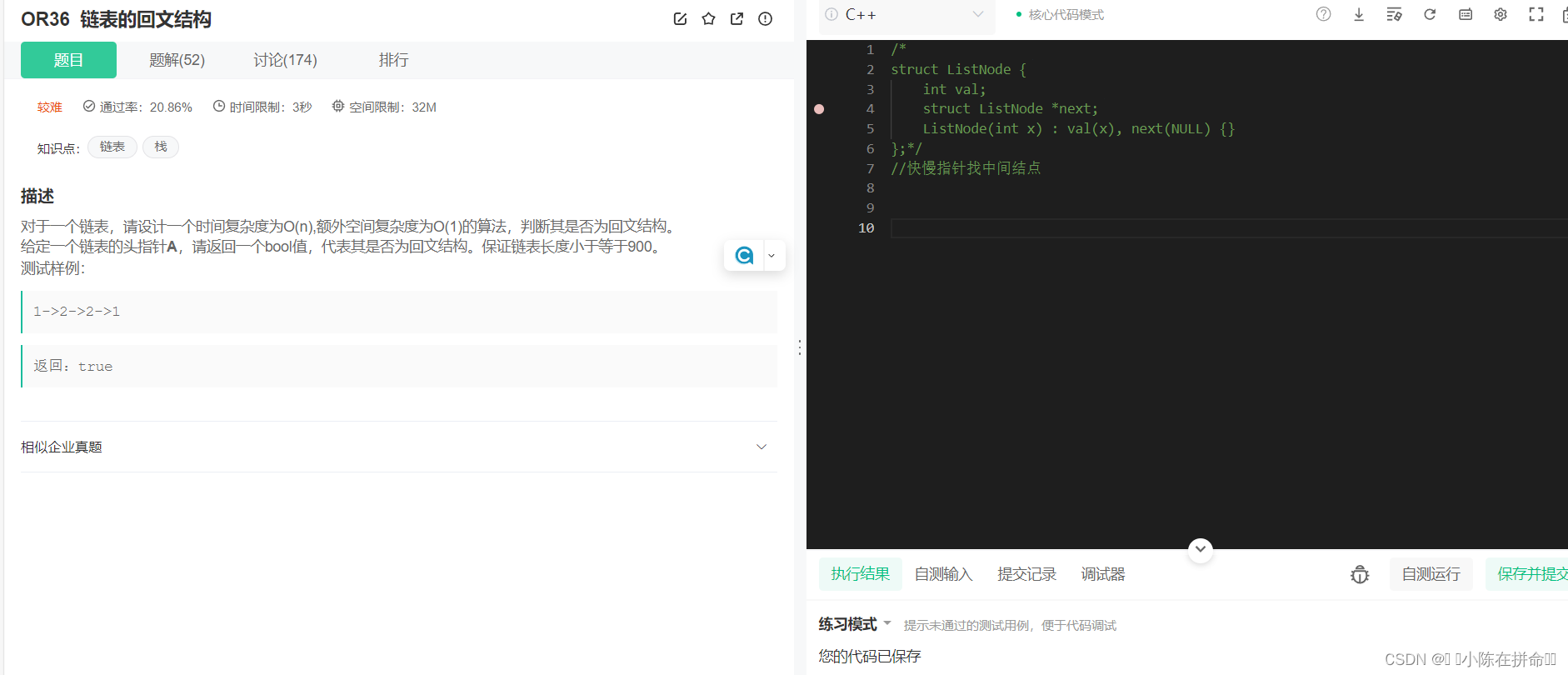
思路1:找到中间结点,然后逆置后半段,然后将后续半段和前半段的链表同时走,如果其中一个走到空了值依旧是相等的,那么就是回文结构!!
空间复杂度:o(N)
时间复杂度:o(1)
ListNode *middleNode(struct ListNode *phead)
{
struct ListNode *fast,*slow;
fast=slow=phead;
while(fast!=NULL&&fast->next!=NULL)
{
fast=fast->next->next;
slow=slow->next;
}
return slow;
}
struct ListNode* reverseList(struct ListNode* head)
{
//链表为空的时候
if(head==NULL)
return head;
//链表不为空的时候,创建3个指针,分别指向前驱、当前、后继结点
struct ListNode*p1,*p2,*p3;
p1=NULL;//前驱
p2=head;//当前
p3=head->next;//后继
while(p2)
{
//改变指向
p2->next=p1;
//向后挪动
p1=p2;
p2=p3;
//考虑p3为NULL的时候
if(p3)
p3=p3->next;
}
return p1;
}
class PalindromeList {
public:
bool chkPalindrome(ListNode* A)
{
struct ListNode *mid=middleNode(A);//找中间结点
struct ListNode *rmid=reverseList(mid);//逆序后半段
while(rmid)
{
if(A->val!=rmid->val)
return false;
A=A->next;
rmid=rmid->next;
}
return true;
}
};六、随机链表的复制(力扣)
经典算法OJ题:随机链表的复制
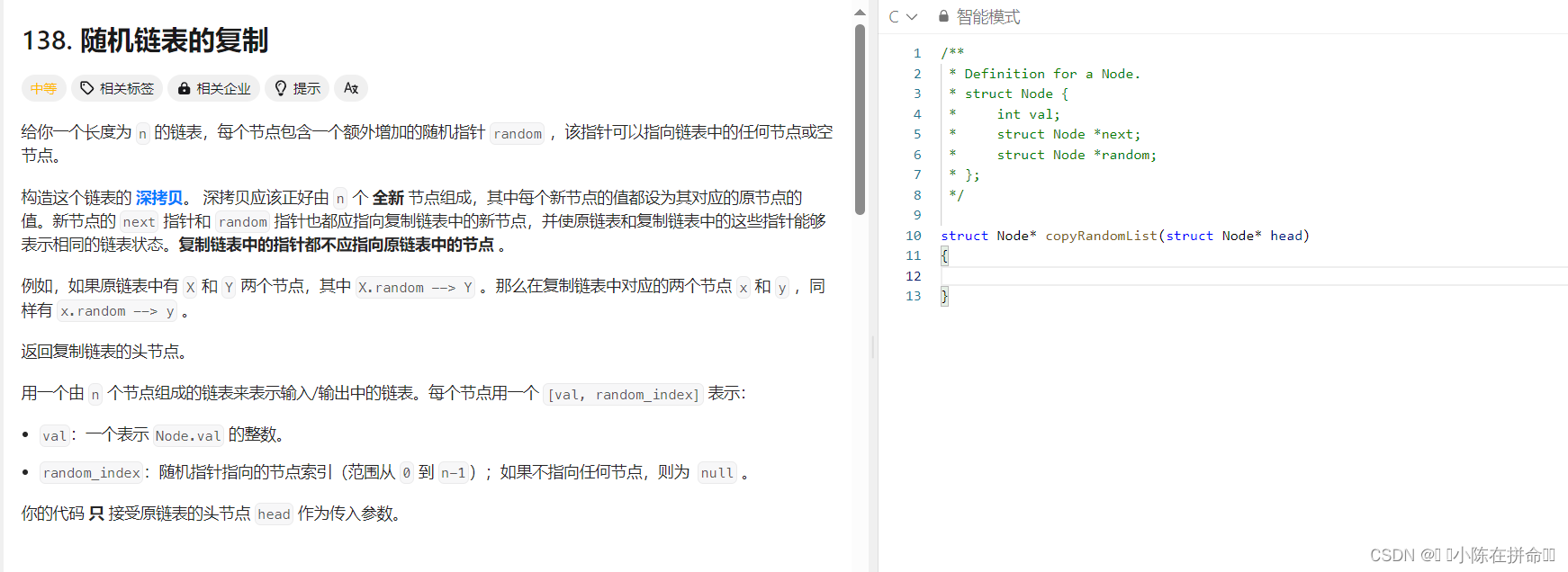
思路1:1、插入拷贝结点到原结点的后面,2、控制拷贝结点的random,3、拷贝结点解下来,尾插到新链表上,同时恢复原链表
空间复杂度:o(N)
时间复杂度:o(N)
typedef struct Node Node;
Node* copyRandomList(Node* head)
{
if(head==NULL)
return NULL;
//将拷贝结点放在原结点的后面
Node*pcur=head;
while(pcur)
{
Node*copy=(Node*)malloc(sizeof(Node));//拷贝结点
copy->val=pcur->val;
//插入
copy->next=pcur->next;
pcur->next=copy;
//迭代
pcur=pcur->next->next;
}
//控制拷贝结点的random指针
pcur=head;
while(pcur)
{
//有可能random指向NULL
Node* copy=pcur->next;
if(pcur->random==NULL)
copy->random=NULL;
else
//拷贝结点的random恰好在原结点的random后面
copy->random=pcur->random->next;
//迭代
pcur=pcur->next->next;
}
//将拷贝结点解下来尾插到新链表上
pcur=head;
Node*newhead,*newtail,*temp;
newhead=newtail=(struct Node*)malloc(sizeof(struct Node));
temp=NULL;//用来记录遍历点
while(pcur)
{
Node* copy=pcur->next;
temp=copy->next;//记录遍历点
newtail->next=copy;//尾插
newtail=newtail->next;
//修复原链表
pcur->next=temp;
//继续遍历
pcur=pcur->next;
}
Node*ret=newhead->next;//销毁哨兵结点前记住头结点
free(newhead);
newhead=NULL;
return ret;
}思路2:暴力拷贝链表,然后看原结点的random是原链表的第几个结点,对应的就是拷贝链表的的第几个结点
空间复杂度:o(N^2)
时间复杂度:o(N)
typedef struct Node Node;
Node* copyRandomList(Node* head)
{
if(head==NULL)
return NULL;
Node*pcur=head;
Node*newhead,*newtail;
newhead=newtail=(Node*)malloc(sizeof(Node));//哨兵结点
while(pcur)
{
Node*newnode=(Node*)malloc(sizeof(Node));
newnode->val=pcur->val;
newtail->next=newnode;
newtail=newnode;
//迭代
pcur=pcur->next;
}
newtail->next=NULL;//要记住最后有个NULL;
pcur=head;//回到链表头
Node*newpcur=newhead->next;//用来遍历新链表头
while(pcur)
{
int s=0;//记录节点与head的距离
Node*flag=head,*temp=pcur->random;//temp记住random结点
while(flag!=temp)
{
++s;
flag=flag->next;
}
flag=newhead->next;//回到新链表的头
while(s--)
flag=flag->next;
//找到了,就接上
newpcur->random=flag;
pcur=pcur->next;
newpcur=newpcur->next;
}
Node*ret=newhead->next;
free(newhead);
newhead=NULL;
return ret;
}七、带环链表的快慢指针追击问题(力扣)
7.1 判断链表中是否有环
经典算法OJ题:判断链表是否带环

思路:快慢指针追击

typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head)
{
ListNode*fast,*slow;
fast=slow=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
return true;
}
return false;
}7.2 返回链表开始入环的第一个结点
思路1:利用相遇点到入口点距离等于链表头到入口点距离的结论
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head)
{
ListNode*fast,*slow;
fast=slow=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
//相等,说明相遇了,链表带环
if(slow==fast)
{
ListNode*meet=slow;
while(meet!=head)
{
meet=meet->next;
head=head->next;
}
return meet;
}
}
return NULL;
}思路2:在相遇点将带环链表拆开,转化成求链表相交结点的问题
typedef struct ListNode ListNode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
ListNode * Apcur=headA;//用来遍历A链表
ListNode * Bpcur=headB;//用来遍历A链表
int a=0;//数a长度
int b=0;//数b长度
while(Apcur)
{
Apcur=Apcur->next;
a++;
}
while(Bpcur)
{
Bpcur=Bpcur->next;
b++;
}
//找最小数,写俩while循环,只要大的数才可以走,小的走不了
int m=a>b?b:a;
while(a-m)
{
headA=headA->next;
a--;
}
while(b-m)
{
headB=headB->next;
b--;
}
while(headA)
{
if(headA==headB)
return headA;
headA=headA->next;
headB=headB->next;
}
return NULL;
}
struct ListNode *detectCycle(struct ListNode *head)
{
ListNode*fast,*slow;
fast=slow=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
//将带环链表的环拆开
ListNode*newhead=slow->next;
slow->next=NULL;
return getIntersectionNode(newhead,head);
}
}
return NULL;
}
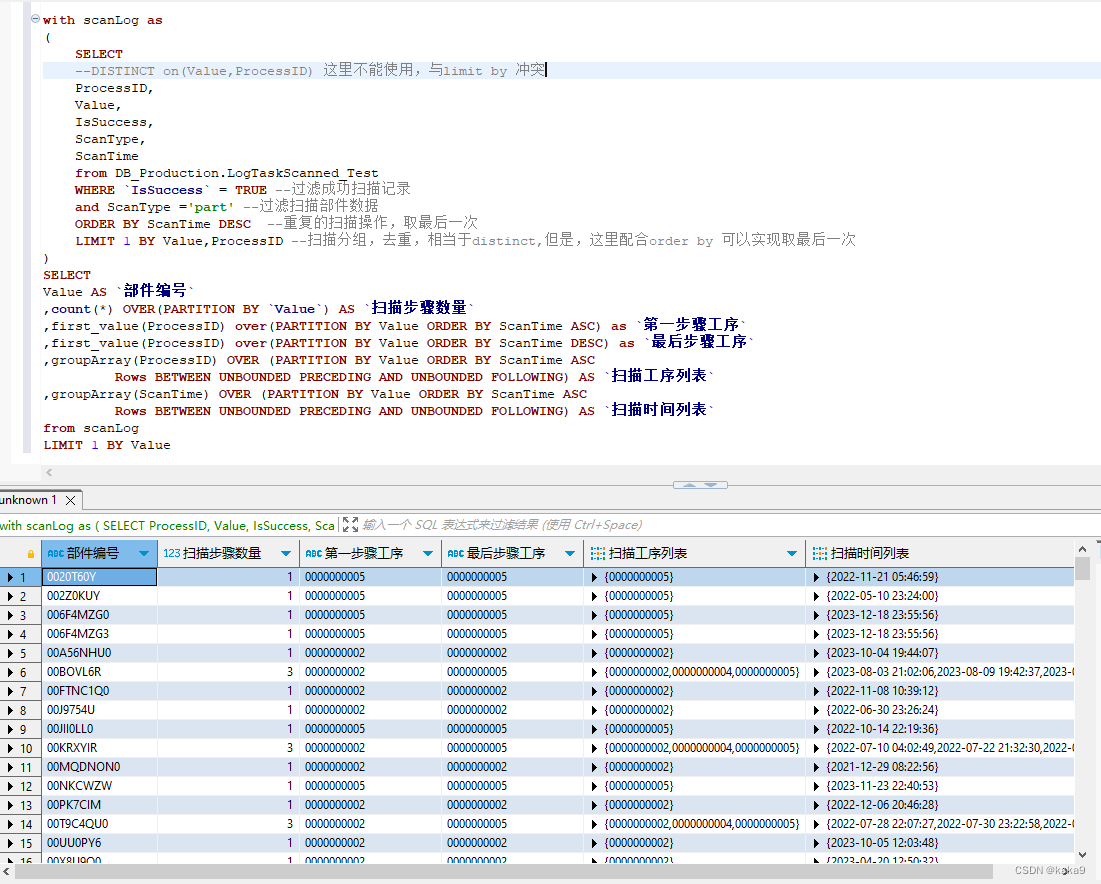
7.3 追击问题扩展
根据前两题可以知道对于带环的链表,fast走2步,slow走1步
1、必然会相遇,不会错过
2、L=(n-1)*C+(C-x) 一个指针从相遇点走,一个指针从链表头走,最后会在入口点相遇
如果fast走3步,slow走1步,可以得到什么结论??








![XCTF:3-1[WriteUP]](https://img-blog.csdnimg.cn/direct/202ba1da85d74bd8badb47397bf73f62.png)