最近在刷一些链表的题目，在leetcode上有一道设计跳表的题目，也是通过查阅各种资料，自己实现出来，感觉这是种很神奇的数据结构。

一.简介

跳表与红黑树，AVL树等，都是一种有序集合，那既然是有序集合，其目的肯定是去奔着提升查找效率而去实现的。

1. 单链表

看下图，比如我要查找1，在链表中第一下就能找到，而要去查找5的话，则是需要遍历完整个链表才能查找到，时间复杂度是O(n）注意如果是增删改的前提不就是需要先查找吗？所以时间复杂度是同样的。

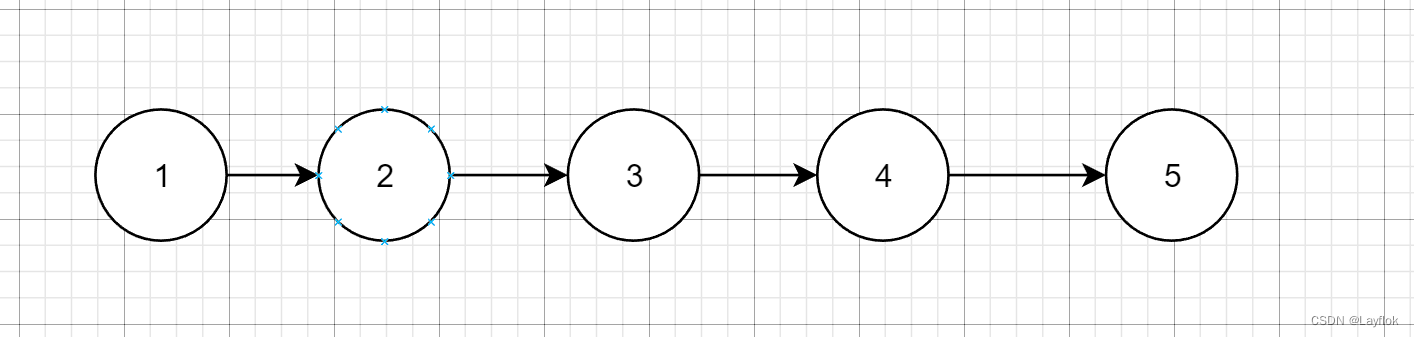
然而我们之前学习的查找算法中，二分查找是非常厉害的，时间复杂度可以到达O(log n)，对数级的时间复杂度相当的快，那么二分思想就是折半，像红黑树，AVL树，B树之类的数据结构，在搜索的时候都是进行折半的搜索，而跳表同样也是O（log n）的时间复杂度。

2. 跳表

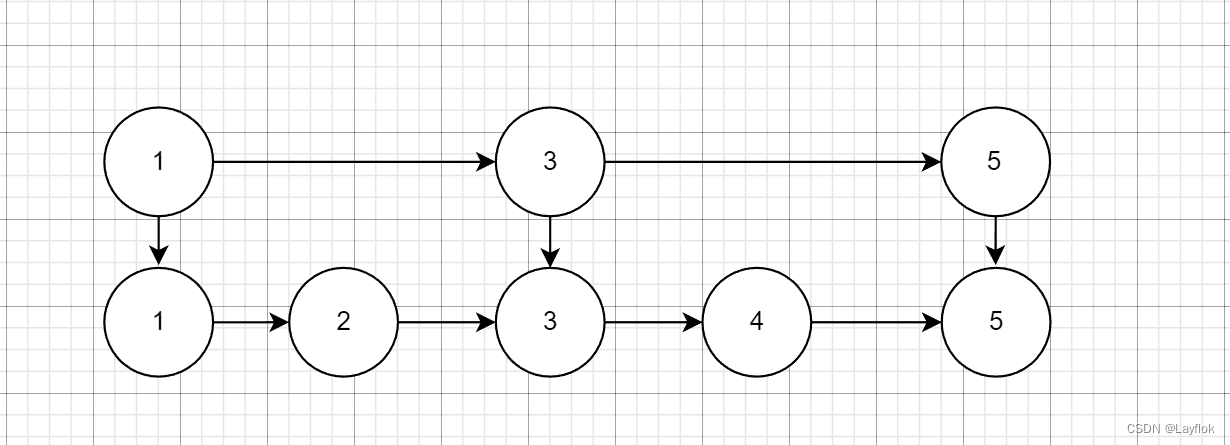
如果需要查找5这个节点，在单链表中需要查找5次，而在下面的跳表中，则需要查找3次就好了，少了一次，可是真的就少一次吗？

拿如果节点多，层数开始往上叠加，就会发现，从1到5，直接少了5次比较。

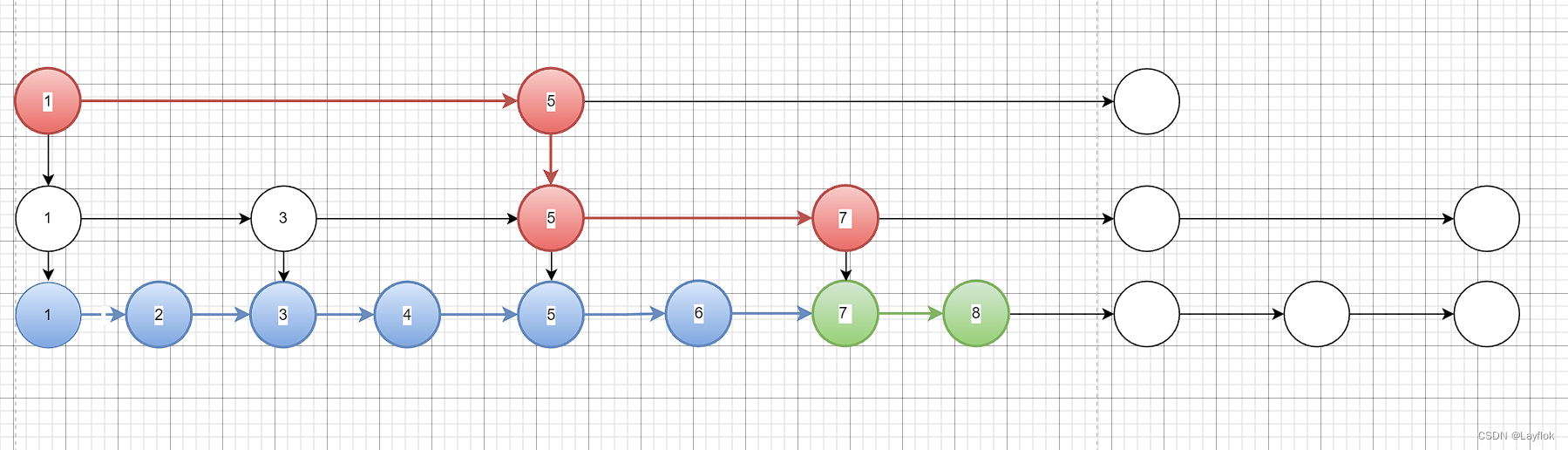
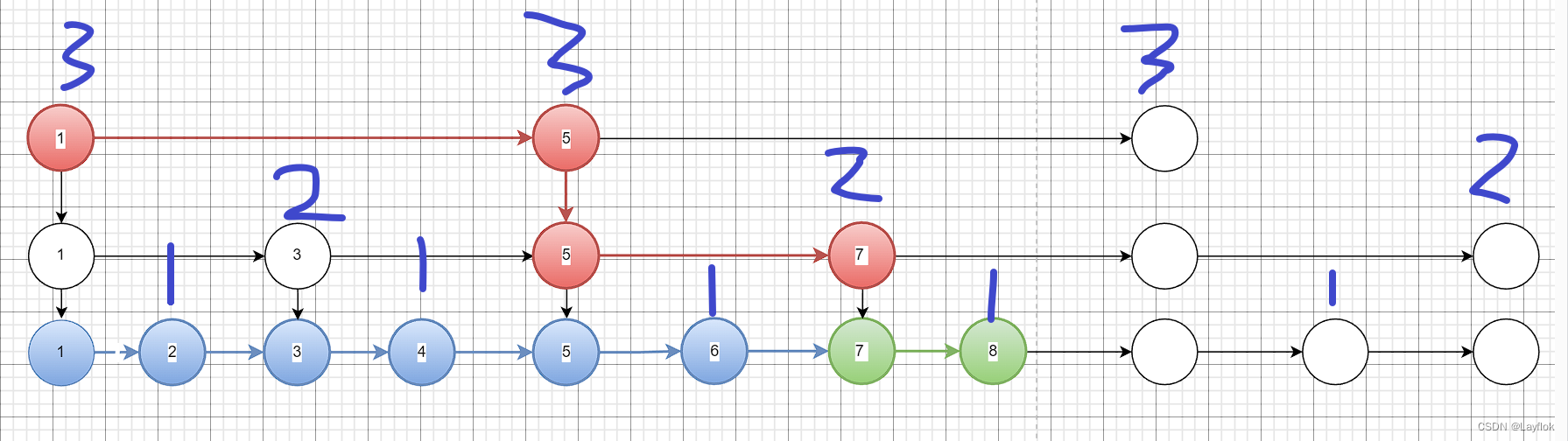
经过一系列的数学证明，它的时间复杂度也是O(log n)的，但是这里肯定就不去证明了😓。
而跳表的结构就是一层一层的，拿空间换取时间。

二. 跳表的结构模型

从上图可以看出，跳表是一层一层的，所以可以用一个需要用到数组来维护。

1. 结构定义

#define MAX_LEVEL 3

typedef struct SkipNode
{
	int val;		//值
	int maxLevel;	//当前节点的最大层数
	//下一个节点的指针数组。
	struct SkipNode** next;
}SkipNode;

typedef struct
{
	int nodeNum;	//节点个数
	int level;		//跳表的索引总层数
	SkipNode* head;
}SkipList;

以上是跳表的结构定义，其中那个Node中maxLevel就是当前这个节点的层数，因为每个节点的层数是不一样的嘛，这个用途呢在后面的删除节点中会用到。

2. 操作函数

下面是针对与跳表的一些操作函数，其中GetRandomLevel这个函数也是我第一次学到，后面进行单独的讲解。
对于跳表的打印函数也没有，是我自己整出来的，方便调试，毕竟都是指针，谁看谁不迷糊啊。

//创建出一个新的节点，将其层数以及值传过来。
SkipNode* BuyNode(int level, int val);

//创建跳表
SkipList* Create();

//传过来一个 target，看看是否在跳表中
bool Search(SkipList* list, int target);

//获取拆入节点时候，所需的层数
int GetRandomLevel();

//将val 插入 跳表中去，
void SkipListAdd(SkipList* list,int val);

//找到节点然后删除
void SkipListDel(SkipList* list, int target);

//打印一下跳表结构
void Print(SkipList* list);

//销毁跳表
void Destroy(SkipList** list

三. 实现操作函数

1. 获取层数（GetRandomLevel）

这个函数的实现也就是短短几行，但是不理解它，很懵，真的很懵，这个函数是获取一个随机的层数，用来开辟新节点的层数。
也能从上述的图片中发现一个问题，就是随着每一个节点的插入，我们改如何取其节点的层数是多少？
每一层呢是一个概率问题，从得二层开始，二分之一，三分之一，四分之一，五分之一等等。。

• 我随机出来一个数这个数只能是0和1，拟定0为当前层，1为下一层.
• 如果我这个数是0，那么就在当前层停下来
• 如果是1，那么就去下一层，接着再随机，使其变成0的时候停下来。
• 然后取当前所随机的层数，要是随机层数大于了最大的层数
• 取当前跳表的层数即可。
• （这里的最大层数是你在文件中所定义的常量 – MAX_LEVEL,而不是说当前跳表的层数）
  下面的动图举了两个例子，分别是2，和3节点。
  节点2，一下子就随机到了0，所以选择1层插入就好了
  节点3，随机了两次不是0，所以自己就加到了3，第三次是0，那么就在选择三层。
  

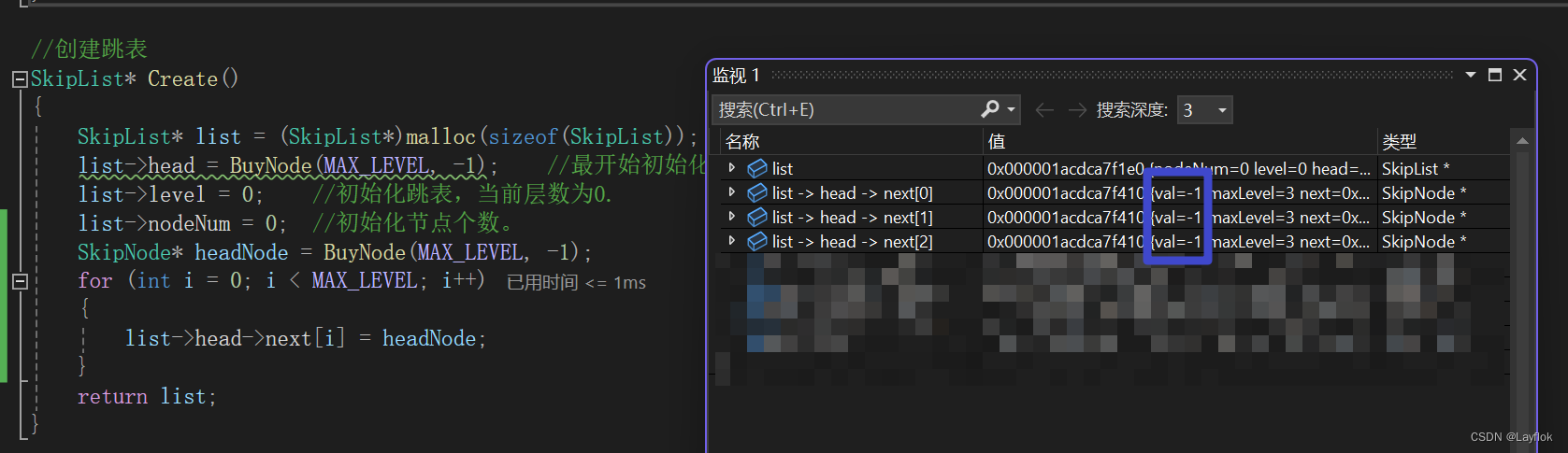
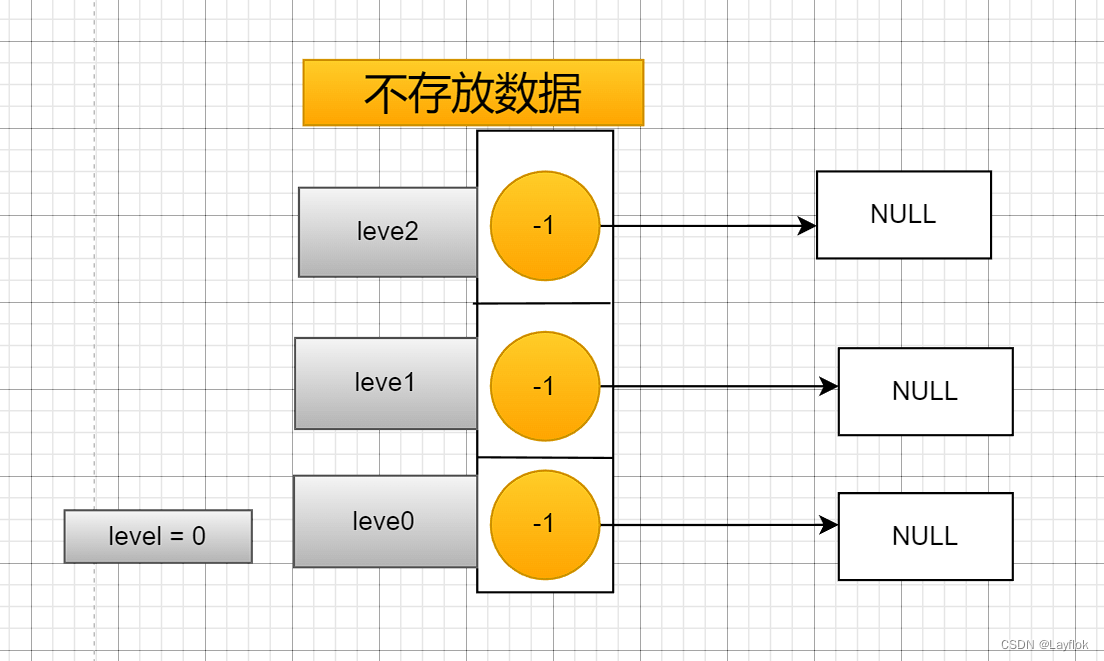
2. 初始化跳表

• 首先对head进行一个BuyNode，这样子就能通过head找到后续的全部节点。
• 然后在对head -> next[i] 就像链表一样，设置一个头节点，这样子方便后续的一些操作。
• 就是下面这两幅图中的样子。
  
  

//创建出一个新的节点，将其层数以及值传过来。
SkipNode* BuyNode(int level, int val)
{
	SkipNode* newNode = (SkipNode*)malloc(sizeof(SkipNode));
	newNode->val = val;
	newNode->maxLevel = level;
	newNode->next = (SkipNode**)malloc(sizeof(SkipNode*) * level);
	for (int i = 0; i < level; i++)
	{
		newNode->next[i] = NULL;
	}
	return newNode;
}

//创建跳表
SkipList* Create()
{
	SkipList* list = (SkipList*)malloc(sizeof(SkipList));
	list->head = BuyNode(MAX_LEVEL, -1);	//最开始初始化开辟5层，可修改，-1无意义，头节点。
	list->level = 0;	//初始化跳表，当前层数为0.
	list->nodeNum = 0;	//初始化节点个数。
	SkipNode* headNode = BuyNode(MAX_LEVEL, -1);
	for (int i = 0; i < MAX_LEVEL; i++)
	{
		list->head->next[i] = headNode;
	}
	return list;
}

3. 插入

对于跳表的插入，其实也是相当于一次查找，所以只要会插入了，就肯定会查找了。
假设跳表是这个样子，需要插入4这个节点。

• 首先呢我们从最高增往下去找，利用cur指针移动,
• 在移动的过程中同时需要拿一个数组prevNodes记录着每一层的前一个节点，然后随着cur的遍历，终究会在最后一层停下来。
  
• 而停下之后，讲意味着找到合适的位置，所以在当前的位置下进行插入节点就好了，而prevNodes就起到了可以是前后链接的作用而链接就跟普通的链表插入一样。

以下是代码，其中还有写细节注释

//将val 插入 跳表中去，
void SkipListAdd(SkipList* list, int val)
{
	//也是从最高层开始
	int levelIndex = list->level - 1;
	SkipNode* cur = list->head->next[levelIndex];
	//开辟一个prev数组，其里面存放着每一层相对应的前一个节点。
	SkipNode** prevNodes = (SkipNode**)malloc(sizeof(SkipNode*) * MAX_LEVEL);	
	int i;
	for (i = levelIndex; i >= 0; i--)
	{
		while (cur->next[i] != NULL && cur->next[i] -> val < val)
		{
			cur = cur->next[i];
		}

		//至此呢，要么找到了当前层数的末尾，要么是找到了合适的位置
		prevNodes[i] = cur;
	}

	//获取随机层数
	int suitLevel = GetRandomLevel();
	if (suitLevel > list->level)
	{
		//当新节点的层数比当前层数大时候，将为赋值的prevNodes[i]记录
		for (i = list -> level; i < suitLevel; i++)
		{
			prevNodes[i] = list->head->next[i];
		}

		//更新层数
		list->level = suitLevel;
	}

	//将前面每层的节点于新节点进行链接
	SkipNode* newNode = BuyNode(suitLevel, val);
	for (i = 0; i < suitLevel; i++)
	{
		newNode->next[i] = prevNodes[i]->next[i];
		prevNodes[i]->next[i] = newNode;
	}

	list->nodeNum++;
}

4. 删除

删除于插入是十分类似的，都是以相同的方式去遍历跳表，同样都是拿prevNodes记录每一层的前一个节点。

• 删除有一种情况就是说，需要删除的数在最高层，那么此时我们需要进行检查，判断时候需要讲那一层删除掉。
• 下图两幅图中，分别对9进行删除，如果删除之后，最高层指向的下一个不是空指针，那么就不需要删除层数，否则就需要讲层数减1
  
  

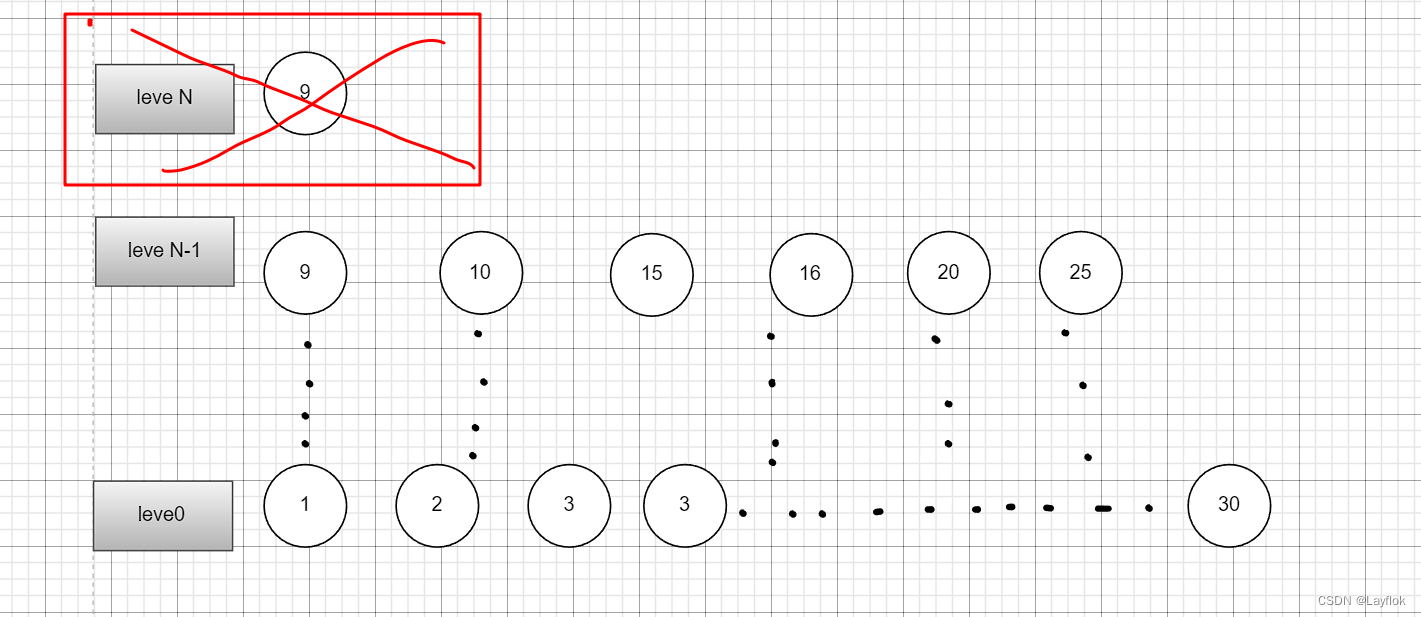
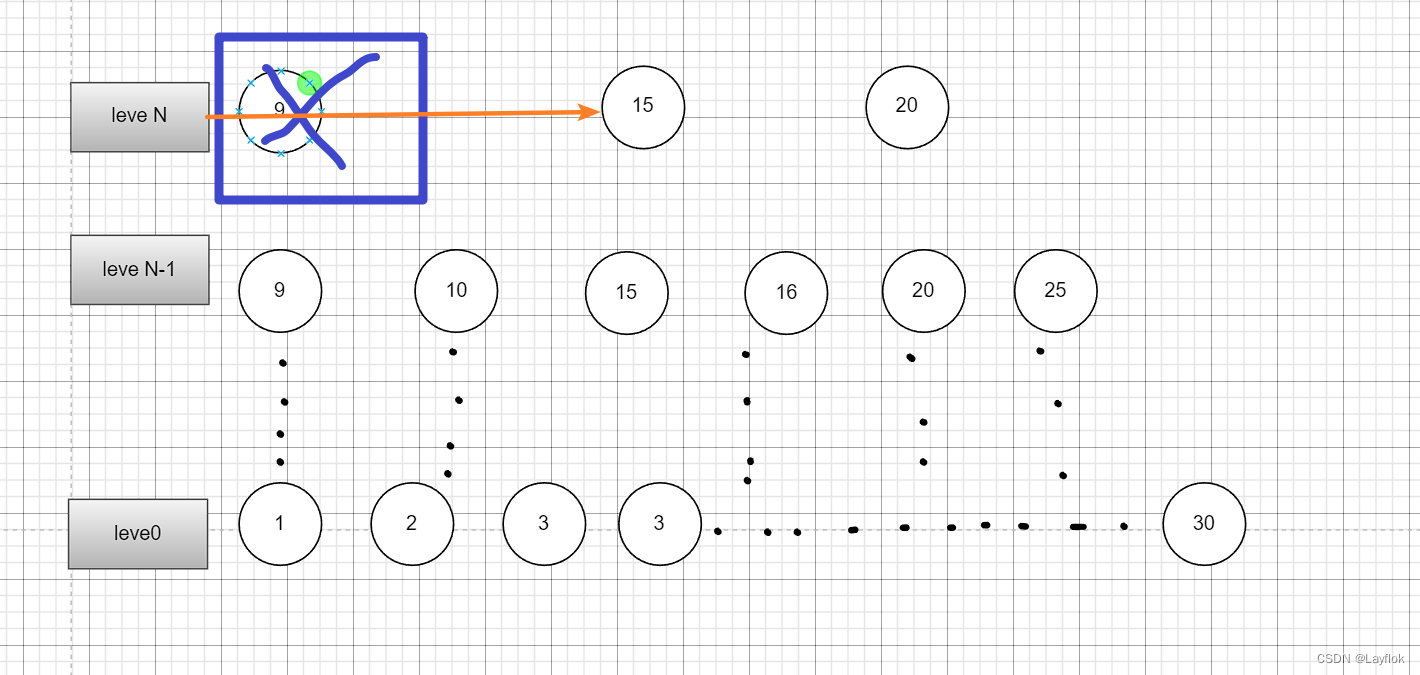
//找到节点然后删除
void SkipListDel(SkipList* list, int target)
{
	if (!Search(list, target))
	{
		printf("%d -> 此节点未找到!\n", target);
		return;
	}

	int levelIndex = list->level - 1;
	SkipNode** prevNodes = (SkipNode**)malloc(sizeof(SkipNode*) * MAX_LEVEL);
	SkipNode* cur = list->head->next[levelIndex];
	int i;
	for (i = levelIndex; i >= 0; i--)
	{
		while (cur->next[i] != NULL && cur->next[i]->val < target)
		{
			cur = cur->next[i];
		}

		prevNodes[i] = cur;
	}

	cur = cur->next[0];

	//将所需要删除节点的以一个和后一个链接起来
	for (i = 0; i < cur->maxLevel; i++)
	{
		prevNodes[i]->next[i] = cur->next[i];
	
	}

	
	//判断删除当前节点后，是否需要更新最高层
	for (i = list -> level - 1; i >= 0; i--)
	{
		if (list->head->next[i]->next[i] != NULL)
		{
			break;
		}
		list->level--;
	}

	free(cur);
	list->nodeNum--;
}

5. 查找

其实我们在进行插入和删除同时就是在反复的做着查找的工作，在遍历的过程中判断合适的位置，重复的去比较大小。

• 如果cur -> next[i] == NULL,直接进入下一层，也就是对循环体进行一个continue；
• 那么如果cur -> next[i] == val, 那么就是找到了。

//传过来一个 target，看看是否在跳表中
bool Search(SkipList* list, int target)
{
	//从最上层开始去找
	int levelIndex = list->level - 1;
	SkipNode* cur = list->head->next[levelIndex];
	int i;
	for (i = levelIndex; i >= 0; i--)
	{
		//下一个如果小于target，就往前一直遍历
		while (cur->next[i] != NULL && cur->next[i]->val < target)
		{
			cur = cur->next[i];
		}
		//至此，要么大于，等于，或者使这一层没有。
		if (cur->next[i] == NULL)
		{
			//直接去下一层
			continue;
		}
		//再去判断是否等于
		if (cur->next[i]->val == target)
		{
			return true;
		}
	}

	return false;
}

6. 销毁

• 销毁跳表的话只能是从第一层了，可不能再从上往下了。

//销毁跳表
void Destroy(SkipList** list)
{
	//从最底层往上
	SkipNode* cur = (*list)->head -> next[0];
	SkipNode* tmp = cur->next[0];
	free((*list)->head);
	while (cur != NULL)
	{
		tmp = cur->next[0];
		free(cur);
		cur = tmp;
	}

	free(*list);
	*list = NULL;
}

至此呢，跳表就是实现完成了，这篇文章也是仅供参考，可能有些测试不准确，或者没有测试到位，有bug欢迎各位在评论区指出。。。

源码链接