话不多说,直接看题:

显然,我们直接用深搜,我们可以先把空位用结构体存,然后打表存小方块,再用数组存行列。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int a[12][12];
int biao[20][20]={{0,0,0,0,0,0,0,0,0,0},
{0,1,1,1,2,2,2,3,3,3},
{0,1,1,1,2,2,2,3,3,3},
{0,1,1,1,2,2,2,3,3,3},
{0,4,4,4,5,5,5,6,6,6},
{0,4,4,4,5,5,5,6,6,6},
{0,4,4,4,5,5,5,6,6,6},
{0,7,7,7,8,8,8,9,9,9},
{0,7,7,7,8,8,8,9,9,9},
{0,7,7,7,8,8,8,9,9,9}
};
int ck[20][20];
int lie[12][12],hang[12][12];
struct node{
int x,y;
}b[200];
int cnt;
void print(void){
for(int i=1;i<=9;i++){
for(int j=1;j<=9;j++){
cout<<a[i][j]<<" ";
}
cout<<endl;
}
}
void dfs(int deep){
if(deep>cnt){
print();
return ;
}
else{
for(int i=1;i<=9;i++){
if(lie[b[deep].y][i]==0&&hang[b[deep].x][i]==0&&ck[biao[b[deep].x][b[deep].y]][i]==0){
lie[b[deep].y][i]=1;
a[b[deep].x][b[deep].y]=i;
hang[b[deep].x][i]=1;
ck[biao[b[deep].x][b[deep].y]][i]=1;
dfs(deep+1);
lie[b[deep].y][i]=0;
hang[b[deep].x][i]=0;
ck[biao[b[deep].x][b[deep].y]][i]=0;
}
}
}
}
int main(){
for(int i=1;i<=9;i++){
for(int j=1;j<=9;j++){
cin>>a[i][j];
if(a[i][j]!=0){
lie[j][a[i][j]]=1;
hang[i][a[i][j]]=1;
ck[biao[i][j]][a[i][j]]=1;
}
else{
b[++cnt].x=i;
b[cnt].y=j;
}
}
}
dfs(1);
}值得注意的,我们其实可以三个判断容器排个序,选出约束条件最多的先枚举,这样虽然复杂度还是一样,但是按照这个顺序就可以更快的确定约束条件多的从而减少不必要的递归次数。
我们可以举个例子:

接题:

下面为分析:
我们写出4与7的组合然后分段计算即可,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
long long l,r;
long long a[7000];
int cnt;
bool cmp(long long a,long long b){
return a<b;
}
void dfs(int deep){
if(deep>500000000000LL) return ;
a[cnt++]=deep;
dfs(10*deep+4);
dfs(10*deep+7);
}
signed main(){
cin>>l>>r;
dfs(0);
sort(a+1,a+cnt,cmp);
int l1=lower_bound(a+1,a+cnt,l)-a;
int r1=lower_bound(a+1,a+cnt,r)-a;
long long sum=0;
if(l1!=r1){
sum+=(a[l1]-l+1)*a[l1];
for(int i=l1+1;i<=r1-1;i++){
sum+=(a[i]-a[i-1])*a[i];
}
sum+=(r-a[r1-1])*a[r1];}
else{
sum=a[r1]*(r-l+1);
}
cout<<sum;
}看道有趣的题:
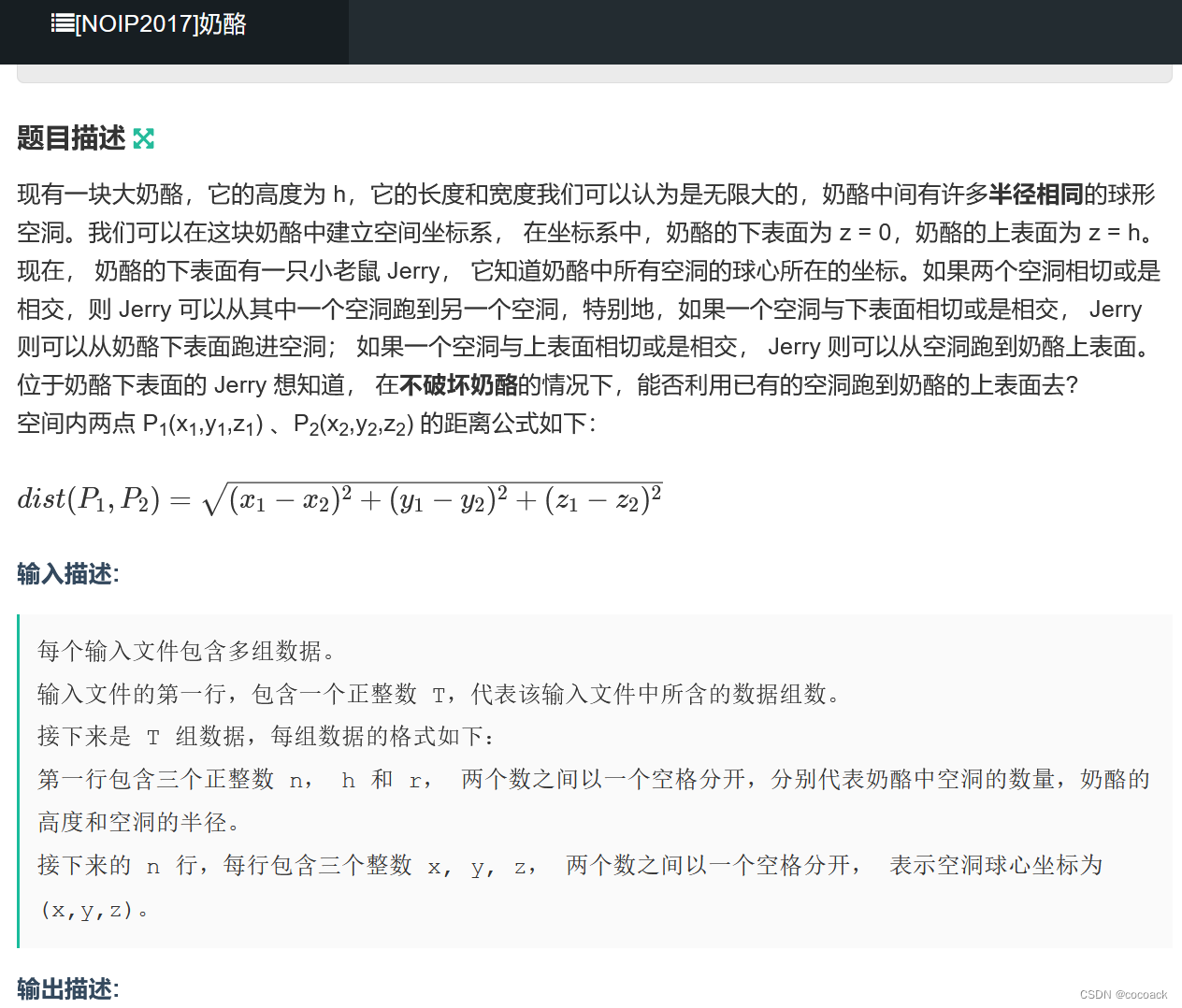
可以用并查集,最后判断与下表面连的点与上表面连的点是否在同一个集合,这里采用BFS,先把与上表面相连的点放队里,在判断与他们相连的点,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int t,n,h,r,b[1010];
struct node{
int x,y,z;
}a[1010];
int check(node a,node b){
if(pow(a.x-b.x,2)+pow(a.y-b.y,2)+pow(a.z-b.z,2)<=4*pow(r,2)){
return 1;
}
return 0;
}
int main(){
cin>>t;
while(t--){
memset(b,0,sizeof(b));
queue<node> q;
int f=0;
scanf("%d%d%d",&n,&h,&r);
for(int i=1;i<=n;i++){
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
if(r+a[i].z>=h){
q.push(a[i]);
b[i]=1;}
}
while(!q.empty()){
node s=q.front();
q.pop();
if(s.z-r<=0){
f=1;
break;
}
for(int i=1;i<=n;i++){
if(b[i]==0&&check(a[i],s)==1){
q.push(a[i]);
b[i]=1;
}
}
}
if(f) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}