第九章 动态规划part02

•  62.不同路径 

  /**
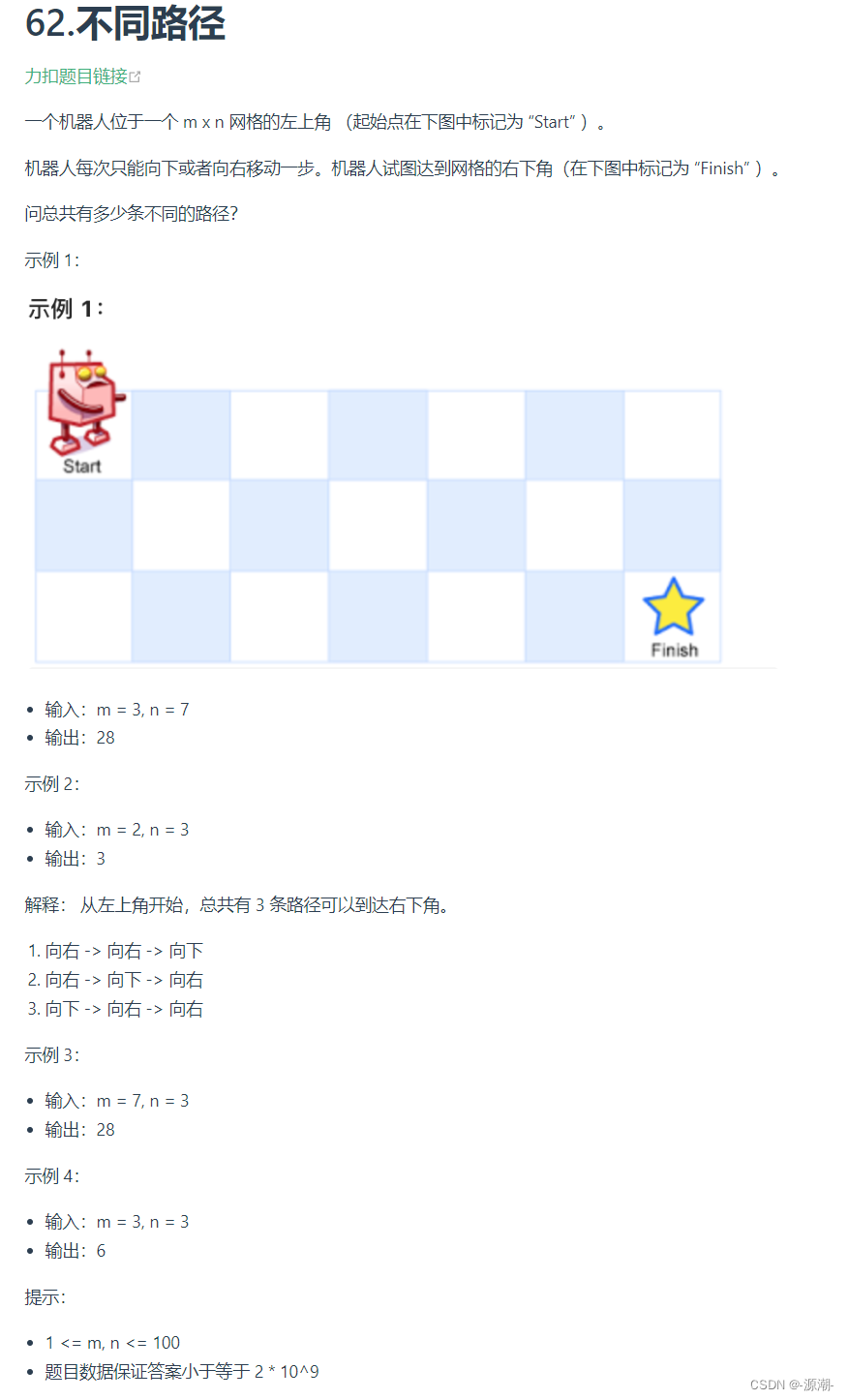
       * 1. 确定dp数组下标含义 dp[i][j] 到每一个坐标可能的路径种类
       * 2. 递推公式 dp[i][j] = dp[i-1][j] dp[i][j-1]
       * 3. 初始化 dp[i][0]=1 dp[0][i]=1 初始化横竖就可
       * 4. 遍历顺序 一行一行遍历
       * 5. 推导结果 。。。。。。。。
       *
       * @param m
       * @param n
       * @return
       */
      public static int uniquePaths(int m, int n) {
          int[][] dp = new int[m][n];
          //初始化
          for (int i = 0; i < m; i++) {
              dp[i][0] = 1;
          }
          for (int i = 0; i < n; i++) {
              dp[0][i] = 1;
          }
  
          for (int i = 1; i < m; i++) {
              for (int j = 1; j < n; j++) {
                  dp[i][j] = dp[i-1][j]+dp[i][j-1];
              }
          }
          return dp[m-1][n-1];
      }

  思路：该题是动态规划的经典题目，关键是动态规划五部曲的应用，首先要确定dp数组和其含义，确定递推公式，初始化dp数组，确定遍历顺序，最后举例推导dp数组。

•  63. 不同路径 II 

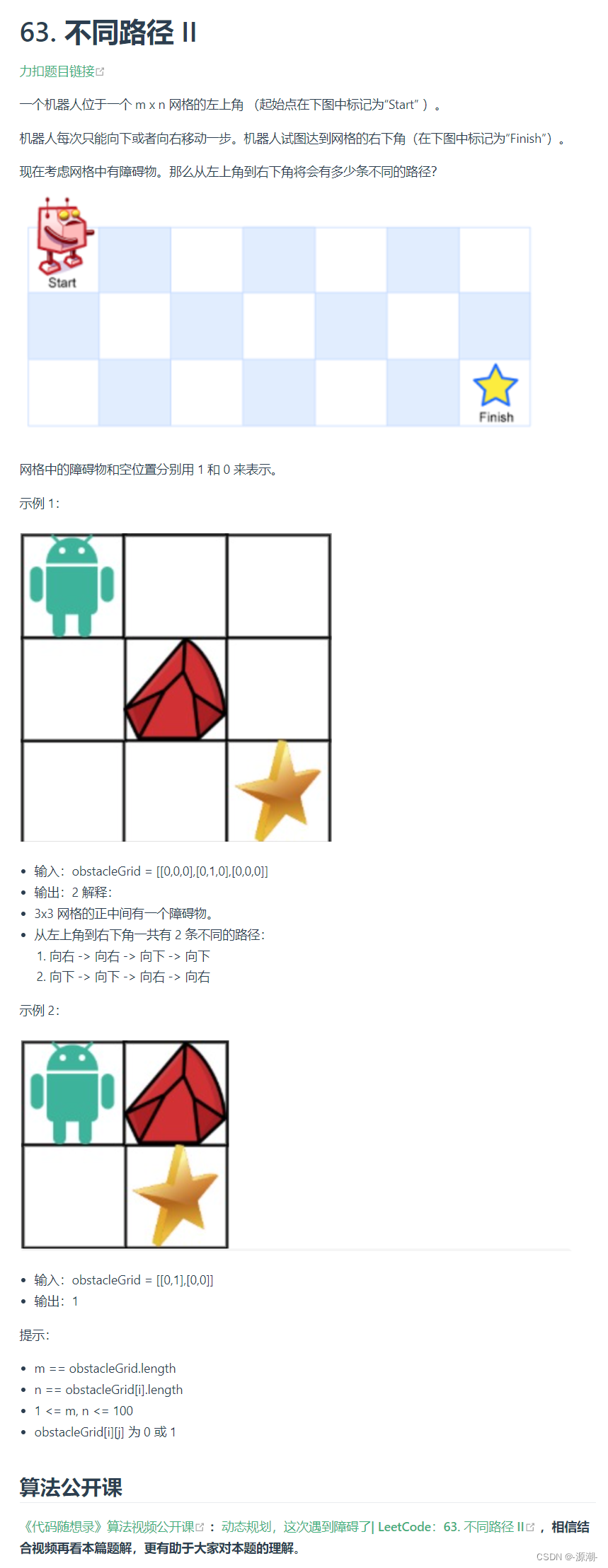
  class Solution {
      public int uniquePathsWithObstacles(int[][] obstacleGrid) {
          int m = obstacleGrid.length;
          int n = obstacleGrid[0].length;
          int[][] dp = new int[m][n];
  
          //如果在起点或终点出现了障碍，直接返回0
          if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
              return 0;
          }
  
          for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
              dp[i][0] = 1;
          }
          for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
              dp[0][j] = 1;
          }
  
          for (int i = 1; i < m; i++) {
              for (int j = 1; j < n; j++) {
                  dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
              }
          }
          return dp[m - 1][n - 1];
      }
  }

  思路：注意！第一行和第一列，只要出现障碍，后边的dp数组都为0；因为第一行和第一列都是由前面走出来的，只要前面出现了障碍，后面都走不通。如果起点或者终点出现了障碍，直接返回0。