简介

决策树作为机器学习的一种经典算法，在数据挖掘、分类和回归等任务中广泛应用。本文将详细介绍机器学习中的决策树算法，包括其原理、构建过程和应用场景。

原理

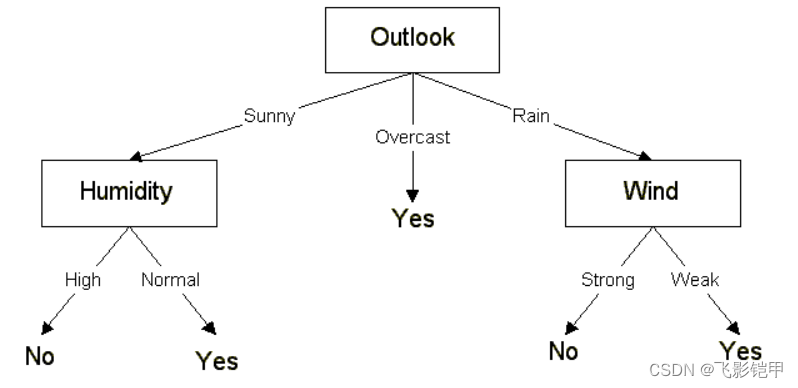
决策树是一种基于树状结构的监督学习算法，它通过构建一棵树来对数据进行分类或回归预测。决策树的每个内部节点代表一个特征属性，每个叶子节点代表一个类别或数值。

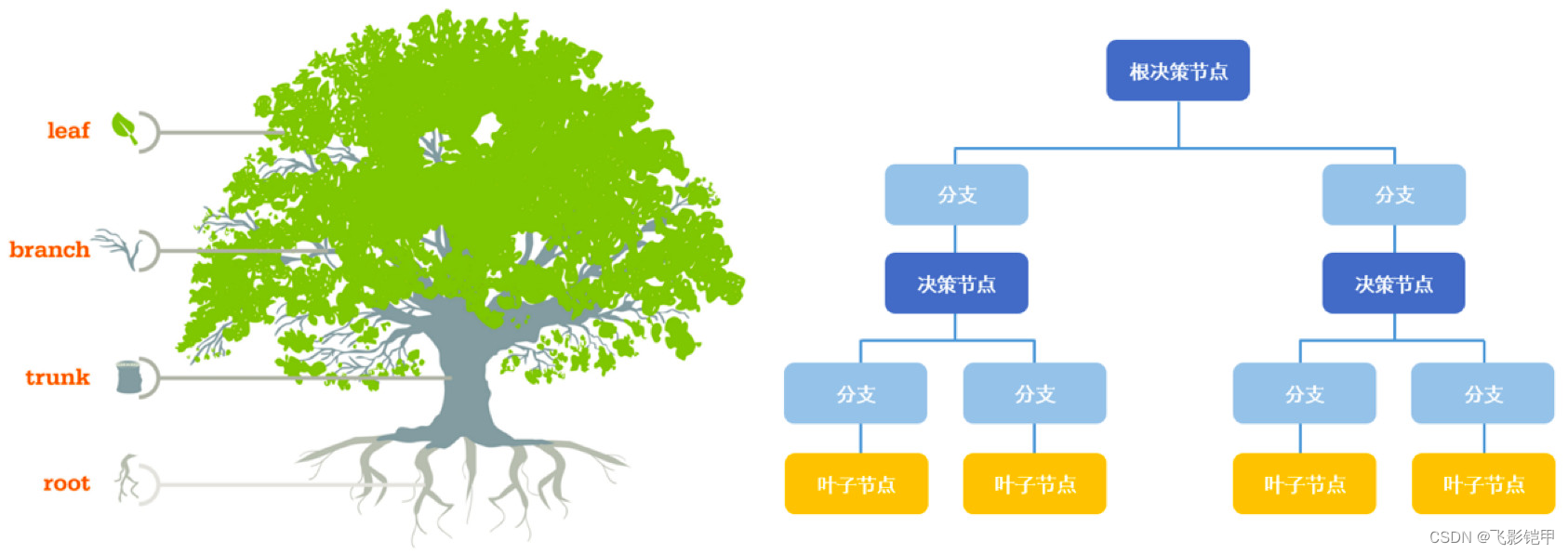
决策树的构建过程：

• 特征选择：根据某种指标选择最佳特征，将数据集划分为不同的子集。
• 决策节点生成：根据选择的特征创建一个决策节点，并将数据集划分到该节点的子节点中。
• 递归构建：对每个子节点递归执行上述步骤，直到满足停止条件（如达到叶子节点或数据集为空）。

构建算法：

决策树的构建过程中有多种算法可供选择，最常见的是ID3、C4.5和CART算法。

• ID3（Iterative Dichotomiser 3）：ID3算法通过信息增益来选择最佳特征。信息增益表示特征对于分类的贡献程度，选择具有最高信息增益的特征作为节点。
• C4.5：C4.5算法在ID3算法的基础上进行了改进，使用信息增益比来选择最佳特征。信息增益比考虑到了特征的取值数目对信息增益的影响，避免了偏向取值较多的特征。
• CART（Classification and Regression Tree）：CART算法可以用于分类和回归任务。它通过基尼系数选择最佳特征，并采用二叉树结构构建决策树。

下面是对ID3算法的详细介绍：

• 熵（Entropy） 在理解ID3算法之前，我们需要先了解熵的概念。熵是信息论中用来衡量系统无序程度的指标。对于一个分类问题，假设有N个样本，其中p个属于类别A，q个属于类别B，则熵可以通过以下公式计算：

Entropy = -p/N * log(p/N) - q/N * log(q/N)

熵越高，表示数据集越无序。

• 信息增益（Information Gain） 信息增益是指在划分数据集前后熵的减少程度，用来衡量选择某个特征进行划分的好坏程度。信息增益可以通过以下公式计算：

Information Gain = Entropy(D) - ∑(|Di|/|D|) * Entropy(Di)

其中，Entropy(D)是划分前整个数据集的熵，|Di|是划分后第i个子集的样本数，Entropy(Di)是第i个子集的熵。

ID3算法步骤 基于上述概念，下面是ID3算法的步骤：

• 步骤1：计算初始数据集的熵，作为根节点的熵。
• 步骤2：对于每个特征，计算其信息增益。
• 步骤3：选择信息增益最大的特征作为当前节点的划分特征。
• 步骤4：根据划分特征的每个取值，将数据集划分为不同的子集。
• 步骤5：对于每个子集，如果所有样本都属于同一类别，则将当前节点标记为叶子节点，类别为该子集中的类别；否则，递归执行步骤2-5。

ID3算法的特点和注意事项

• 特点：
  • ID3算法倾向于选择具有较多取值的特征，因为这些特征通常具有更高的信息增益。
  • ID3算法在处理缺失值时存在困难，因为它无法处理缺失值的情况。
  • ID3算法容易过拟合，即模型过于复杂而无法泛化到新数据。
• 注意事项：
  • ID3算法在处理连续特征时需要进行离散化处理。
  • ID3算法对于有噪声和冲突的数据敏感，可能导致错误分类。
  • ID3算法可以通过设置递归终止条件（如达到叶子节点或数据集为空）来避免过拟合。

应用场景

决策树算法在各个领域都有广泛的应用，包括但不限于以下几个方面：

• 数据挖掘：决策树可以用于发现数据中隐藏的模式和规律，帮助解决分类、聚类等问题。
• 医学诊断：决策树可以根据患者的症状和检查结果进行分类，辅助医生进行疾病诊断。
• 金融风险评估：决策树可以根据客户的个人信息和信用记录进行风险评估，帮助银行和金融机构进行信贷决策。
• 推荐系统：决策树可以根据用户的历史行为和偏好进行推荐，提供个性化的商品或服务推荐。

总结

决策树作为一种简单、直观且易于解释的机器学习算法，具有广泛的应用前景。通过选择合适的特征和构建有效的决策树模型，我们可以从复杂的数据中提取有用的信息，并为决策提供科学依据。随着机器学习领域的不断发展，决策树算法也将继续演化和优化，为各个领域的问题解决提供更加准确和高效的方法。