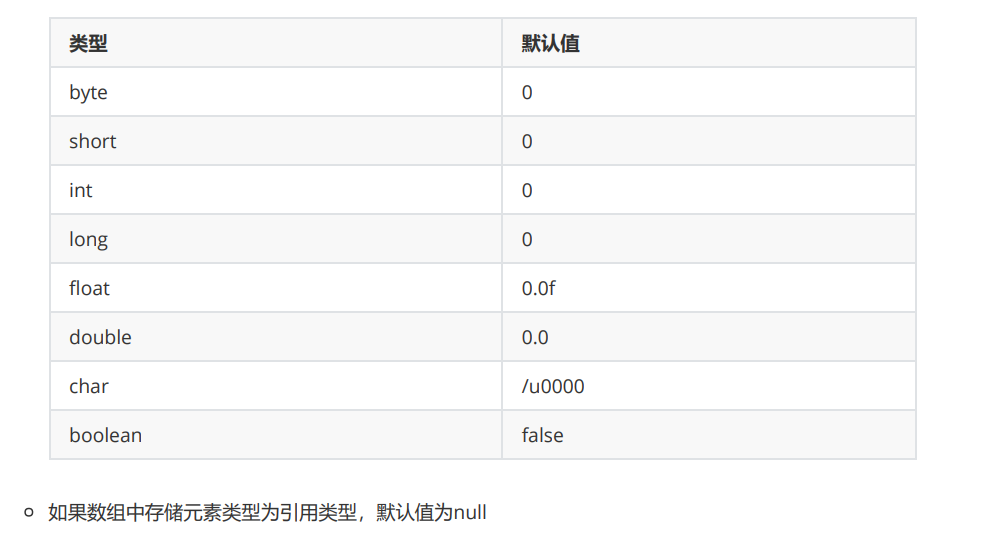
思路一：暴力破解，两个二维数组记录行、列对应的数字出现的次数，比如rows[i][index]表示的数字index在i行出现的次数，三维数组记录每个块中对应数字出现的次数，比如boxes[i/3][j/3][index]表示的数字index在[i/3][j/3]个块中出现的次数，然后进行判断可以得出结果，超过1则不符合代码如下：

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        vector<vector<int>> rows(9,vector<int>(9));
        vector<vector<int>> cols(9,vector<int>(9));
        vector<vector<vector<int>>> subboxes(9,vector<vector<int>>(9,vector<int>(9)));
        for(int i = 0; i<9;i++){
            for(int j = 0; j<9;j++){
                char c = board[i][j];
                if(c!='.'){
                    int index = c - '0' -1;
                    rows[i][index]++;
                    cols[j][index]++;
                    subboxes[i/3][j/3][index]++;
                    if(rows[i][index] > 1 || cols[j][index] > 1||subboxes[i/3][j/3][index]>1){
                        return false;
                    }
                }
            }
        }
        return true;

    }
};

思路二：对思路1进行优化

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        //用于存储行、列、块的数字1-9出现的次数，默认为0
        vector<vector<int>> rows(9,vector<int>(9,0));
        vector<vector<int>> cols(9,vector<int>(9,0));
        vector<vector<int>> boxes(9,vector<int>(9,0));
        //遍历整个格子
        for(int i = 0;i < 9;i++){
            for(int j = 0;j<9;j++){
                //如果为空则跳过
                if(board[i][j] == '.') continue;
                //得到具体的数字，-1的原因是数独的数字是1到9，而我们数组下标为0到8
                int index = board[i][j] - '1';
                //如果当前的数字在之前出现过，则返回失败
                if(rows[i][index]) return false;
                if(cols[j][index]) return false;
                //j/3 + (i/3)*3   如果是j/3 + i的话  (0,2)的位置本应该是0号块，就变成了2号块
                if(boxes[j/3 + (i/3)*3][index]) return false;

                //记录当前遍历的节点的数字的次数
                rows[i][index] = 1;
                cols[j][index] = 1;
                boxes[j/3 + (i/3)*3][index] = 1;
            }
        }
        return true;
    }
};