概念
- 什么是后缀表达式?
- 后缀表达式,其实就是一个中缀表达式 AOB => ABO (A、B是式子、O 为运算符),将运算符向后放
中转后举例
-
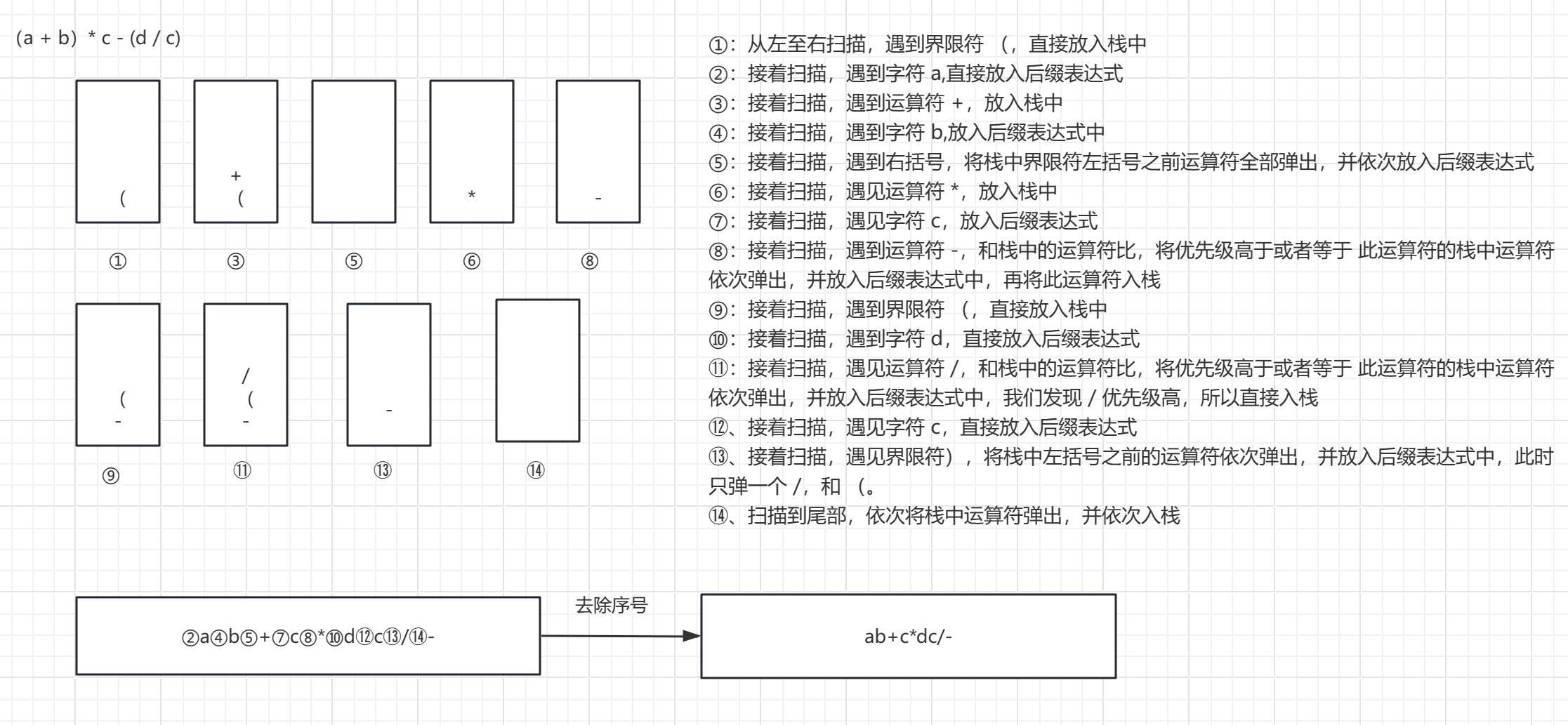
中缀表达式:(a + b)* c - (d / c)
-
首先,我们可以看到,在这个算式中,根据运算规则最先运算的是 括号中的内容,也就是 (a + b), 根据概念,此时 A = a、 B = b、 O = +,AOB=>ABO=>ab+
-
其次,我们将 (ab+) 看作一个整体,式子变成 (ab+)c - (d/c),根据运算规则和优先级,我们可以发现接下来要运算的是 * , 此时A = (ab+)、 B = c 、O = * , AOB => ABO => ab+c
-
紧接着,此式变成了 (ab+c*) - (d/c),根据运算规则和优先级,我们可以发现接下来要运算的是 / ,那么此时 A=d、B=c、O=/ 。AOB=>ABO=>dc/
-
最后,此式变成了,(ab+c*) - (dc/),我们可以发现接下来要运算的是 - ,那么此时 A=(ab+c*)
B= (dc/), O=- 。AOB=>ABO=>ab+c*dc/-(后缀表达式)
-
综上,我们可以看出,其实中缀转后缀,就是根据运算规则,找到我们表达式中最先计算的两项和运算符,然后,将其运算符放后边,并且要保持 A 和 B 的相对顺序不变,依次执行,直到转化成后缀表达式
中缀转后缀过程
详细规则:
- 初始化一个栈,存储 运算符
- 从左到右扫描(依次向后放字符)
- 遇到操作数。直接加入后缀表达式
- 遇到界限符。遇到 “(” 直接入栈,遇到 “)” 则依次弹出栈内运算符并加入后缀表达式,直到弹出 “(” 为止 。注意:“( )” 不加入后缀表达式
- 遇到运算符。依次弹出栈中优先级高于或者等于当前运算符的所有运算符,并加入后缀表达式,若碰到 “(” 或 栈空则停止。之后再把当前运算符入栈。
- 处理完所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式
详细执行过程:
Code
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_SIZE 100
// 运算符优先级函数
int precedence(char op) {
if (op == '+' || op == '-') {
return 1;
} else if (op == '*' || op == '/') {
return 2;
} else {
return 0;
}
}
// 中缀转后缀实现
void infix_to_postfix(char* infix, char* postfix) {
char stack[MAX_SIZE]; // 定义一个栈,用来存放 运算符
int top = -1; // 定义 栈顶指针
int i, j;
// 遍历中缀字符数组
for (i = 0, j = 0; infix[i] != '\0'; ++i) {
// 判断,如果是字符,将其存入后缀字符数组中
if (infix[i] >= 'a' && infix[i] <= 'z') {
postfix[j++] = infix[i];
} else if (infix[i] == '(') { // 如果是 左括号,放入栈中
stack[++top] = infix[i];
} else if (infix[i] == ')') { // 如果是 右括号
// 将栈中 左括号之前的 运算符依次弹出,并进入后缀数组中
while (top != -1 && stack[top] != '(') {
postfix[j++] = stack[top--];
}
// 再减一次是为了:弹出 左括号
top--;
} else {
// 栈不空,并且当栈顶运算符优先级 大于等于 扫描到中缀运算符优先级,将栈中元素依次弹出,放入后缀数组中
while (top != -1 && precedence(stack[top]) >= precedence(infix[i])) {
postfix[j++] = stack[top--];
}
// 再将,扫描到中缀运算符,放入栈中
stack[++top] = infix[i];
}
}
// 当扫描完后,将栈中元素依次弹出,并放入后缀表达式数组中
while (top != -1) {
postfix[j++] = stack[top--];
}
// 设置字符数组结束符
postfix[j] = '\0';
}
int main() {
char infix[MAX_SIZE];
char postfix[MAX_SIZE];
printf("输入中缀表达式: ");
scanf("%s", infix);
infix_to_postfix(infix, postfix);
printf("后缀表达式是: %s\n", postfix);
return 0;
}