神经网络的基本单元是神经元,本节我们介绍神经元的结构。
2.1 神经元
一个神经元是由下面 5 部分组成的:
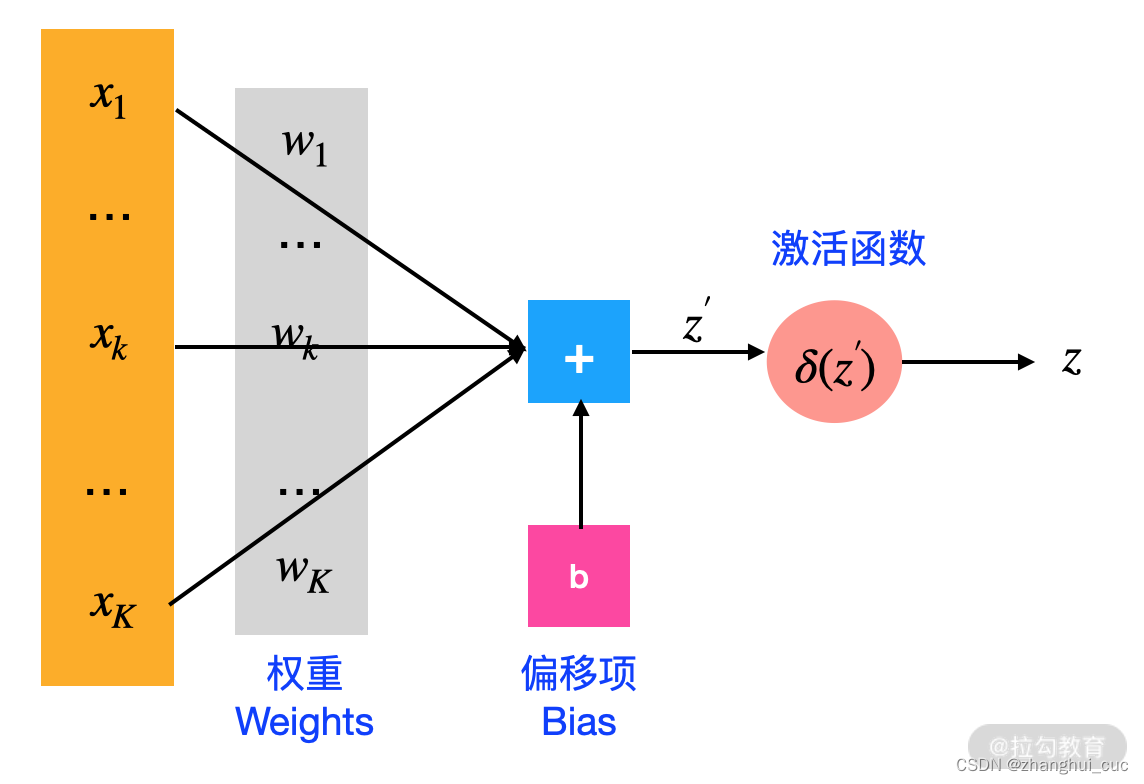
- 输入:x1,x2,…,xk。
- 权重:w1,w2,…,wk。权重的个数与神经元输入的个数相同。
- 偏移项:可省略。
- 激活函数:一般都会有,根据实际问题也是可以省略的。
- 输出。
2.2 激活函数
激活函数有很多种,不同的激活函数适用于不同的问题。二分类问题我们一般采用 Sigmoid 函数,多分类问题我们采用 Softmax 函数,卷积神经网络的中间层一般会采用 relu 函数。下面我们来看看这些激活函数
2.2.1 Sigmoid函数
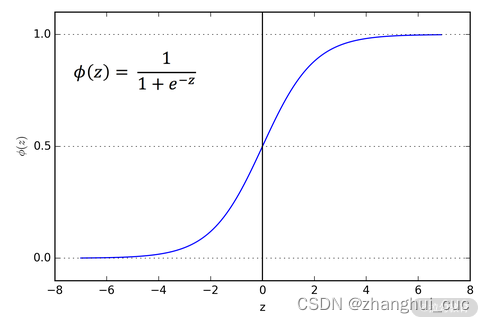
Sigmoid 函数经常被使用在二分类问题,它可以将 1 个数值转换为概率。当输出的概率大于 0.5 或者某一个自定的阈值时,我们就可以判断该类别为正例。不过,现在 Sigmoid 的使用率在逐渐减少,因为会导致梯度消失和爆炸问题。
2.2.2 Softmax函数
Softmax 函数可以将一组数值映射到[0,1]区间内,并且保证输出的和是 1,输出的数值可以看作“概率”。
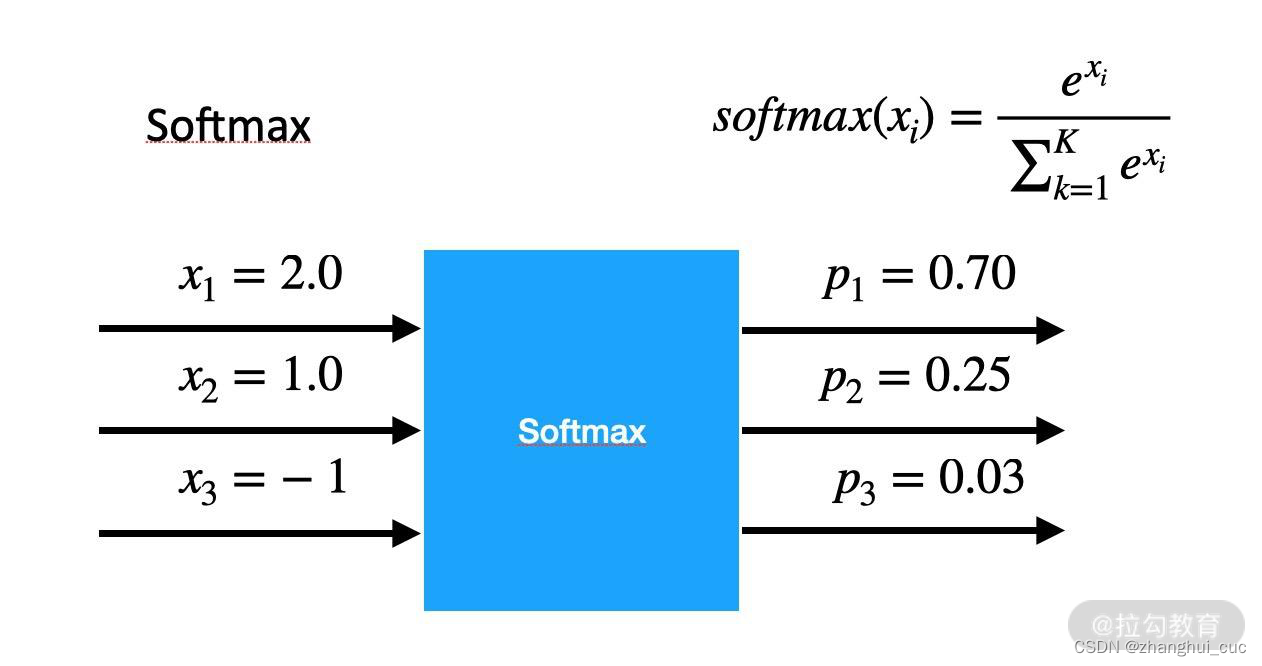
2.2.3 tanh函数
tanh 是双曲函数中的一个,为双曲正切。
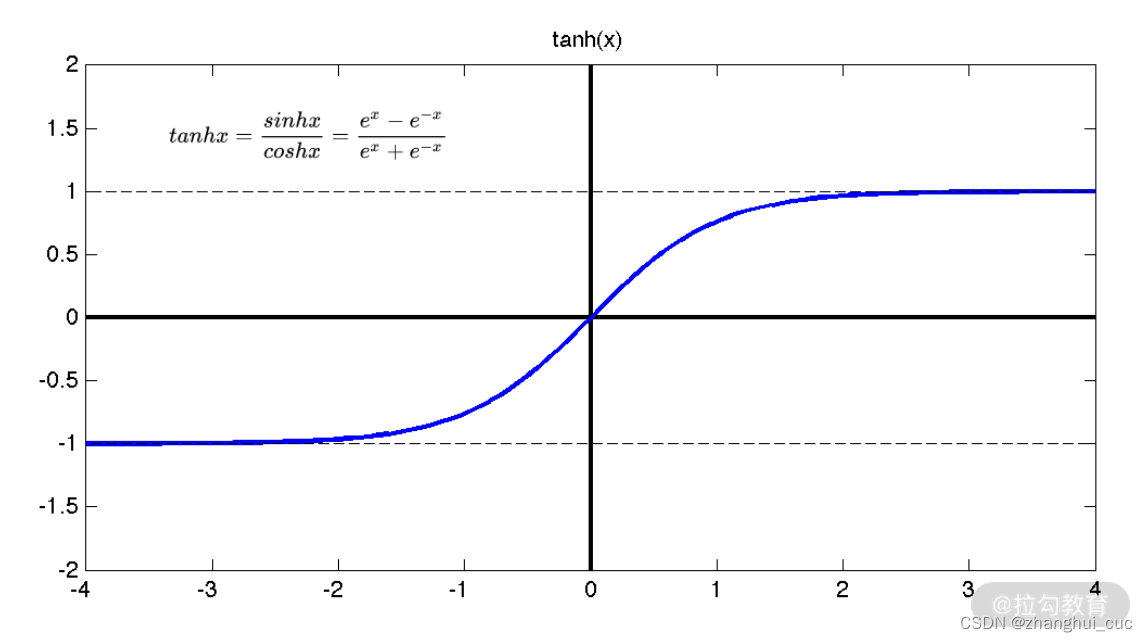
跟 Sigmoid 一样,tanh 函数求导之后的值域仍然在 0~1 之间,所以它也没有解决梯度和幂运算计算量大的问题。
2.2.4 ReLU函数
ReLU 函数又称修正线性单元,是一种人工神经网络中常用的激活函数。ReLU 的公式非常简单:Relu=max(0,x)。从图可以看到,当 x≤0 的时候,函数等于 0,而 x>0 的时候,函数的值就是 x。
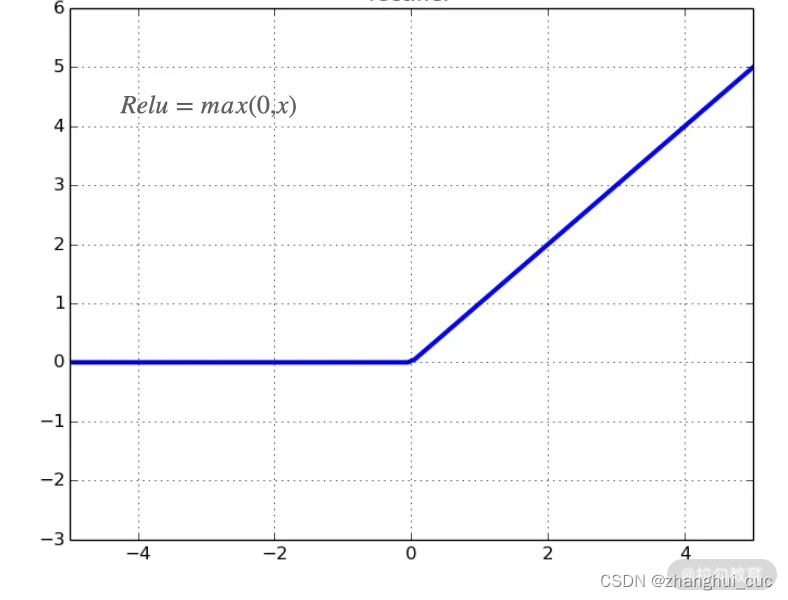
ReLU 函数不仅很大程度上解决了梯度消失的问题,还有着非常快的计算速度,因为它只需要判断是否大于 0 就行了。
当然,它也不是完美的,“ReLU 死区”就是一个很常见的问题,即:在训练一段时间以后,如果某个神经元在某次权重更新之后为负数,那它的激活函数就只会输出 0,这意味着这个神经元“死”掉了,以后再也不会输出其他的值了。例如,在一些特殊的情况下,比如学习率太大,就很容易导致更新后权值为负,从而引发神经元的“死亡”。
2.2.5 Leaky ReLU
为了解决 ReLU 的致命缺点,脱胎于 ReLU 的 Leaky ReLU 函数应运而生,它的公式是f(x)=max(αx,x)。
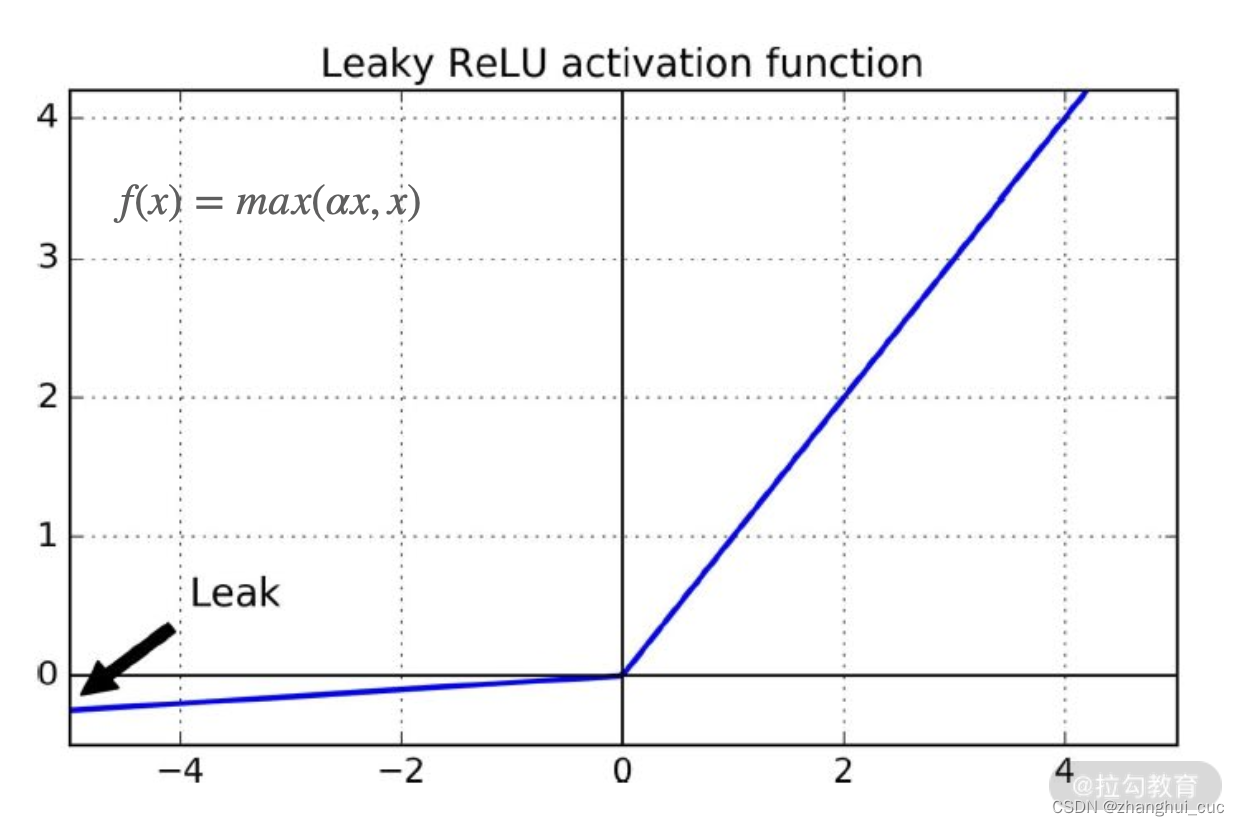
α 是一个超参数,定义了 x<0 时的斜率,比如 0.01。这个小的斜率可以保证激活函数不会出现神经元“死亡”的情况。
2.3 感知机
一个单层的神经网络(只有1个隐藏层)即被称为感知机,而多层感知机就是最简单的神经网络结构。
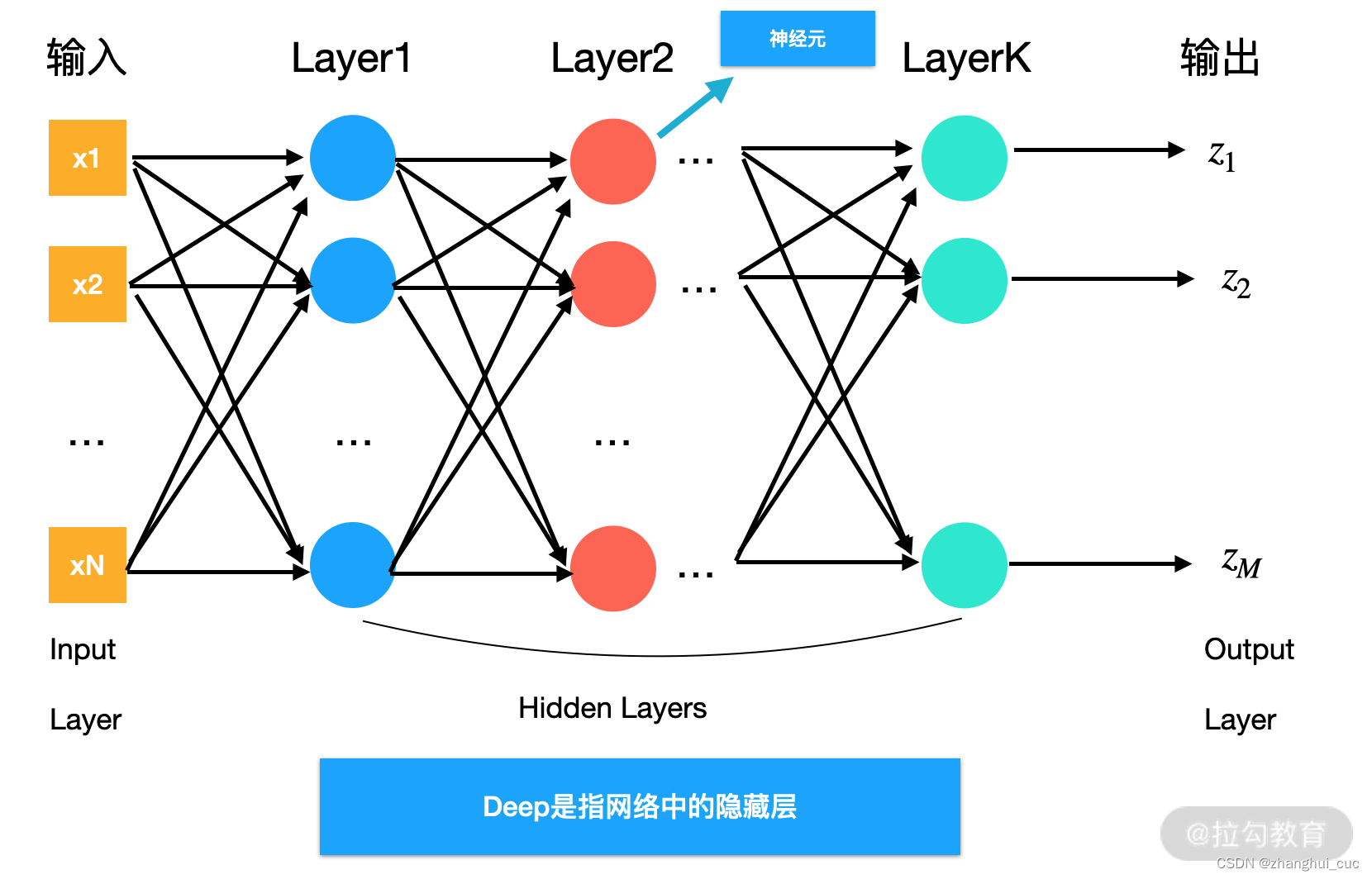
多层感知机是为了解决单个神经元无法学习非线性关系的问题而诞生的,背后的数学解释是当我们有足够多个线性关系的时候,可以拟合出任意的非线性关系的,但是神经元的个数和网络层数不能无限增加,深度学习则解决了这些问题。