1.题目

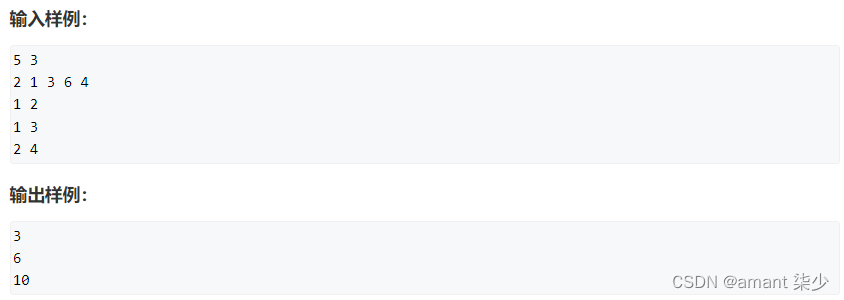
输入一个长度为n的整数序列。
接下来再输入m个询问，每个询问输入一对l，r。
对于每个询问，输出原序列中从第l个数到第 r 个数的和。

输入格式
第一行包含两个整数n和m。
第二行包含n个整数，表示整数数列。
接下来m行，每行包含两个整l和r，表示一个询问的区间范围。

输出格式
共m行，每行输出一个询问的结果。

数据范围
$1\le l\le r\le n，$
$1\le n，m\le 100000，$
$-1000\le 数列中元素的值\le 1000$

2.基本思想

前缀和

原数组: a[1], a[2], a[3], a[4], a[5], …, a[n]
前缀和 Si为数组的前 i项和
前缀和: S[i] = a[1] + a[2] + a[3] + … + a[i]

注意: 前缀和的下标一定要从 1开始, 避免进行下标的转换

s[0] = 0
s[1] = a[1]
s[2] = a[1] + a[2]

基本思路
我们用数组s，每一个si都满足si=si−1+ai。
也就是说，s数组的每一个位置i都表示前i个数的和，故叫前缀和。
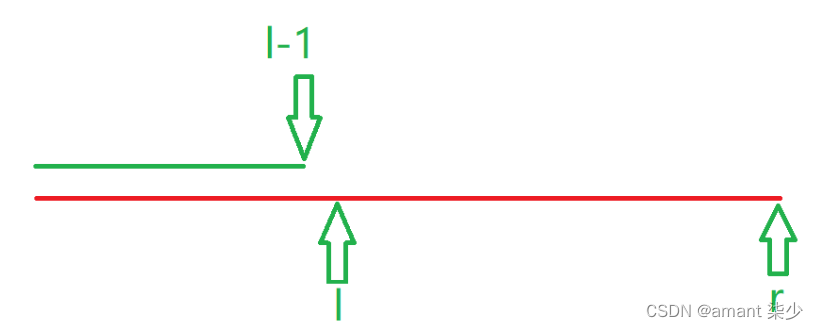
比如我们要求区间 $[l,r]$ 的和，假设我们已经算好s数组。

只要红色部分减去绿色部分，红色部分是s_r，绿色部分是s_l−1，所以sum_l,r=s_r−s_l−1。

3.代码实现

import java.util.Scanner;

public class _795前缀和 {
    static Scanner sc = new Scanner(System.in);
    static int a[] = new int[100010];//原数组
    static int s[] = new int[100010];//前缀和数组

    public static void main(String[] args) {
        int n = sc.nextInt();
        int m = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            a[i] = sc.nextInt();
            s[i] = s[i - 1] + a[i];
        }
        //循环m次查询
        while (m-- >= 0) {
            int l = sc.nextInt();
            int r = sc.nextInt();
            System.out.println(s[r] - s[l-1]);
        }
    }
}

4.总结

1.前缀和的作用

快速求出元素组中某段区间的和
前缀和是一种能够在O(n)O(n)的预处理，O(1)O(1)的查询每段区间的和的一个算法