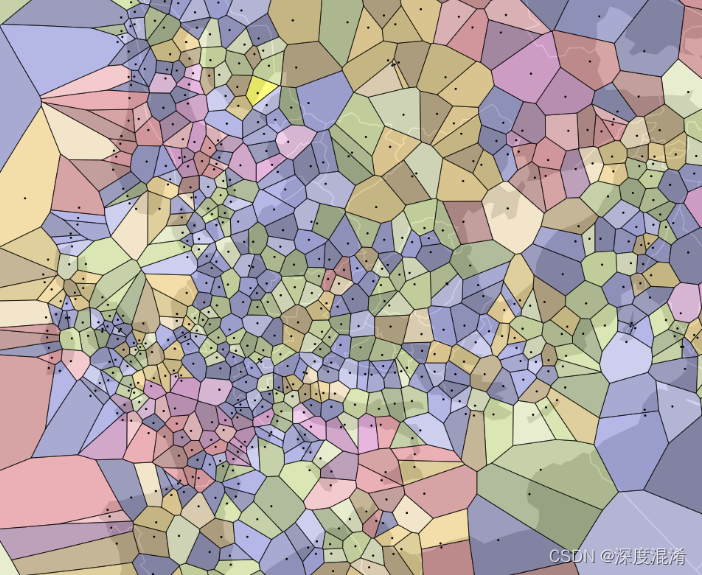
一、三角剖分Delaunay算法简介

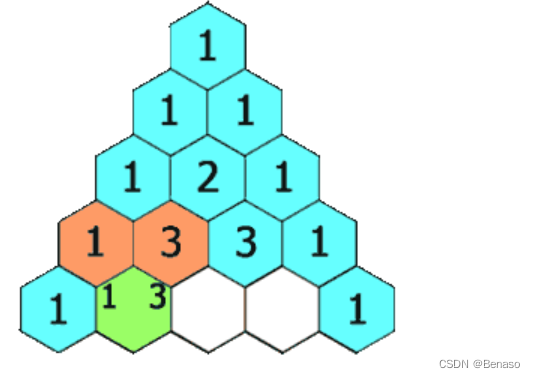
点集的三角剖分(Triangulation),对数值分析(比如有限元分析)以及图形学来说,都是极为重要的一项预处理技术。尤其是Delaunay三角剖分,由于其独特性,关于点集的很多种几何图都和Delaunay三角剖分相关,如Voronoi图,EMST树,Gabriel图等。Delaunay三角剖分有最大化最小角,“最接近于规则化的“的三角网和唯一性(任意四点不能共圆)两个特点。

EMST(Euclidean minimum spanning tree)
Delaunay 三角剖分广泛应用于许多不同应用程序中的科学计算。虽然有大量的计算三角剖分的算法,但 Delaunay 三角剖分以其实用的几何属性广受欢迎。

Gabriel Graph
基本属性是 Delaunay 规则。如果是二维三角剖分,通常将其称为空外接圆规则。对于一组二维点而言,这些点的 Delaunay 三角剖分可确保与每个三角形相关的外接圆的内部都不包含其他点。这种三角剖分便是 Delaunay 三角剖分。
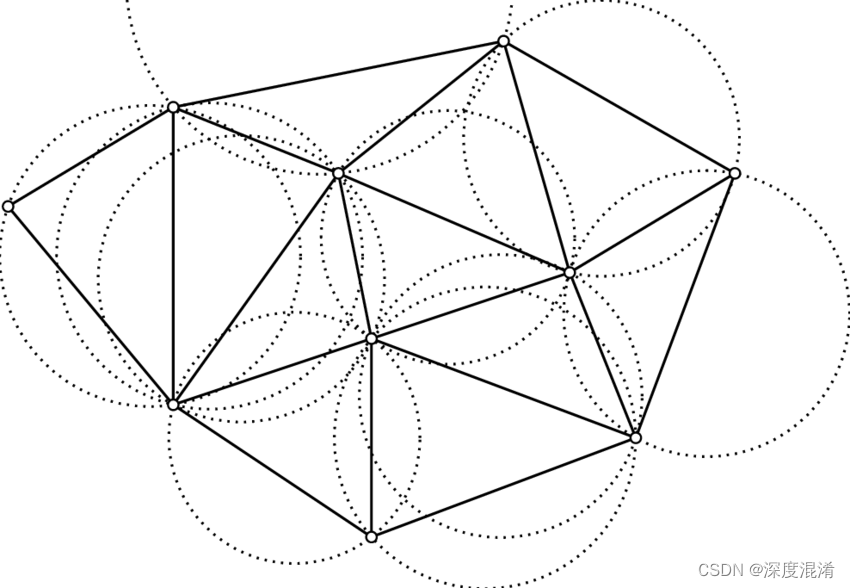
Delaunay 三角剖分堪称“外形整齐”,原因在于为满足空外接圆属性,优先选择带有较大内角的三角形,而不是带有较小内角的三角形。非 Delaunay 三角剖分中的三角形在顶点 V2 和 V4 处呈锐角。如果将 {V2, V4} 边替换为连接 V1 和 V3 的边,会实现最小角的最大化并且使得该三角剖分变为 Delaunay 三角剖分。另外,Delaunay 三角剖分将最近邻点的点连接在一起。这两个特征(外形整齐和最近邻点关系)在实践中具有重要的作用,有助于促进在散点数据插值中使用 Delaunay 三角剖分。
虽然 Delaunay 属性定义明确,但存在退化点集时三角剖分的拓扑并不唯一。在二维中,4 个或更多特征点位于同一圆中时会引发退化。例如,正方形的顶点不具有唯一的 Delaunay 三角剖分。
二、三角剖分Delaunay算法的源代码
namespace Legalsoft.Truffer.Algorithm
{
public struct Vertex
{
public int x;
public int y;
public int z;
}
public struct Triangle
{
public int vv0;
public int vv1;
public int vv2;
}
public class Delaunay
{
public const int MaxVertices = 500;
public const int MaxTriangles = 1000;
public Vertex[] Vertex = new Vertex[MaxVertices];
public Triangle[] Triangle = new Triangle[MaxTriangles];
private bool InCircle(int xp, int yp, int x1, int y1, int x2, int y2, int x3, int y3, double xc, double yc, double r)
{
double eps;
double m1;
double m2;
double mx1;
double mx2;
double my1;
double my2;
double dx;
double dy;
double rsqr;
double drsqr;
eps = 0.000000001;
if (Math.Abs(y1 - y2) < eps && Math.Abs(y2 - y3) < eps)
{
MessageBox.Show("INCIRCUM - F - Points are coincident !!");
return false;
}
if (Math.Abs(y2 - y1) < eps)
{
m2 = (-(Convert.ToDouble(x3) - Convert.ToDouble(x2)) / (Convert.ToDouble(y3) - Convert.ToDouble(y2)));
mx2 = Convert.ToDouble((x2 + x3) / 2.0);
my2 = Convert.ToDouble((y2 + y3) / 2.0);
xc = Convert.ToDouble((x2 + x1) / 2.0);
yc = Convert.ToDouble(m2 * (xc - mx2) + my2);
}
else if (Math.Abs(y3 - y2) < eps)
{
m1 = (-(Convert.ToDouble(x2) - Convert.ToDouble(x1)) / (Convert.ToDouble(y2) - Convert.ToDouble(y1)));
mx1 = Convert.ToDouble((x1 + x2) / 2.0);
my1 = Convert.ToDouble((y1 + y2) / 2.0);
xc = Convert.ToDouble((x3 + x2) / 2.0);
yc = Convert.ToDouble(m1 * (xc - mx1) + my1);
}
else
{
m1 = (-(Convert.ToDouble(x2) - Convert.ToDouble(x1)) / (Convert.ToDouble(y2) - Convert.ToDouble(y1)));
m2 = (-(Convert.ToDouble(x3) - Convert.ToDouble(x2)) / (Convert.ToDouble(y3) - Convert.ToDouble(y2)));
mx1 = Convert.ToDouble((x1 + x2) / 2.0);
mx2 = Convert.ToDouble((x2 + x3) / 2.0);
my1 = Convert.ToDouble((y1 + y2) / 2.0);
my2 = Convert.ToDouble((y2 + y3) / 2.0);
xc = Convert.ToDouble((m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 - m2));
yc = Convert.ToDouble(m1 * (xc - mx1) + my1);
}
dx = (Convert.ToDouble(x2) - Convert.ToDouble(xc));
dy = (Convert.ToDouble(y2) - Convert.ToDouble(yc));
rsqr = Convert.ToDouble(dx * dx + dy * dy);
r = Convert.ToDouble(Math.Sqrt(rsqr));
dx = Convert.ToDouble(xp - xc);
dy = Convert.ToDouble(yp - yc);
drsqr = Convert.ToDouble(dx * dx + dy * dy);
if (drsqr <= rsqr)
{
return true;
}
return false;
}
private int WhichSide(int xp, int yp, int x1, int y1, int x2, int y2)
{
double equation;
equation = ((Convert.ToDouble(yp) - Convert.ToDouble(y1)) * (Convert.ToDouble(x2) - Convert.ToDouble(x1))) - ((Convert.ToDouble(y2) - Convert.ToDouble(y1)) * (Convert.ToDouble(xp) - Convert.ToDouble(x1)));
if (equation > 0)
{
return -1;
}
else if (equation == 0)
{
return 0;
}
else
{
return 1;
}
}
public int Triangulate(int nvert)
{
bool[] Complete = new bool[MaxTriangles];
long[,] Edges = new long[3, MaxTriangles * 3 + 1];
int Nedge;
int xmin;
int xmax;
int ymin;
int ymax;
int xmid;
int ymid;
double dx;
double dy;
double dmax;
int i;
int j;
int k;
int ntri;
double xc = 0.0;
double yc = 0.0;
double r = 0.0;
bool inc;
xmin = Vertex[1].x;
ymin = Vertex[1].y;
xmax = xmin;
ymax = ymin;
for (i = 2; i <= nvert; i++)
{
if (Vertex[i].x < xmin)
{
xmin = Vertex[i].x;
}
if (Vertex[i].x > xmax)
{
xmax = Vertex[i].x;
}
if (Vertex[i].y < ymin)
{
ymin = Vertex[i].y;
}
if (Vertex[i].y > ymax)
{
ymax = Vertex[i].y;
}
}
dx = Convert.ToDouble(xmax) - Convert.ToDouble(xmin);
dy = Convert.ToDouble(ymax) - Convert.ToDouble(ymin);
if (dx > dy)
{
dmax = dx;
}
else
{
dmax = dy;
}
xmid = (xmax + xmin) / 2;
ymid = (ymax + ymin) / 2;
Vertex[nvert + 1].x = Convert.ToInt64(xmid - 2 * dmax);
Vertex[nvert + 1].y = Convert.ToInt64(ymid - dmax);
Vertex[nvert + 2].x = xmid;
Vertex[nvert + 2].y = Convert.ToInt64(ymid + 2 * dmax);
Vertex[nvert + 3].x = Convert.ToInt64(xmid + 2 * dmax);
Vertex[nvert + 3].y = Convert.ToInt64(ymid - dmax);
Triangle[1].vv0 = nvert + 1;
Triangle[1].vv1 = nvert + 2;
Triangle[1].vv2 = nvert + 3;
Complete[1] = false;
ntri = 1;
for (i = 1; i <= nvert; i++)
{
Nedge = 0;
j = 0;
do
{
j = j + 1;
if (Complete[j] != true)
{
inc = InCircle(Vertex[i].x, Vertex[i].y, Vertex[Triangle[j].vv0].x, Vertex[Triangle[j].vv0].y, Vertex[Triangle[j].vv1].x, Vertex[Triangle[j].vv1].y, Vertex[Triangle[j].vv2].x, Vertex[Triangle[j].vv2].y, xc, yc, r);
if (inc)
{
Edges[1, Nedge + 1] = Triangle[j].vv0;
Edges[2, Nedge + 1] = Triangle[j].vv1;
Edges[1, Nedge + 2] = Triangle[j].vv1;
Edges[2, Nedge + 2] = Triangle[j].vv2;
Edges[1, Nedge + 3] = Triangle[j].vv2;
Edges[2, Nedge + 3] = Triangle[j].vv0;
Nedge = Nedge + 3;
Triangle[j].vv0 = Triangle[ntri].vv0;
Triangle[j].vv1 = Triangle[ntri].vv1;
Triangle[j].vv2 = Triangle[ntri].vv2;
Complete[j] = Complete[ntri];
j = j - 1;
ntri = ntri - 1;
}
}
}
while (j < ntri);
for (j = 1; j <= Nedge - 1; j++)
{
if (Edges[1, j] != 0 && Edges[2, j] != 0)
{
for (k = j + 1; k <= Nedge; k++)
{
if (Edges[1, k] != 0 && Edges[2, k] != 0)
{
if (Edges[1, j] == Edges[2, k])
{
if (Edges[2, j] == Edges[1, k])
{
Edges[1, j] = 0;
Edges[2, j] = 0;
Edges[1, k] = 0;
Edges[2, k] = 0;
}
}
}
}
}
}
for (j = 1; j <= Nedge; j++)
{
if (Edges[1, j] != 0 && Edges[2, j] != 0)
{
ntri = ntri + 1;
Triangle[ntri].vv0 = Edges[1, j];
Triangle[ntri].vv1 = Edges[2, j];
Triangle[ntri].vv2 = i;
Complete[ntri] = false;
}
}
}
i = 0;
do
{
i = i + 1;
if (Triangle[i].vv0 > nvert || Triangle[i].vv1 > nvert || Triangle[i].vv2 > nvert)
{
Triangle[i].vv0 = Triangle[ntri].vv0;
Triangle[i].vv1 = Triangle[ntri].vv1;
Triangle[i].vv2 = Triangle[ntri].vv2;
i = i - 1;
ntri = ntri - 1;
}
}
while (i < ntri);
return ntri;
}
}
}
——————————————————————
POWER BY 315SOFT.COM &
TRUFFER.CN