这里写目录标题
- 质数(素数)
- 定义
- 判断是否为质数
- 暴力写法,试除法
- 基本思想
- 具体写法
- 优化
- 基本思想(时间复杂度根号n)
- 具体写法
- 分解质因数
- 分析题意
- 暴力写法
- 基本思想
- 具体代码
- 优化
- 基本思想(时间复杂度小于等于根号n)
- 具体代码
- 筛质数(区别于判断质数,这个是筛选出来并保存,质数的数目较多)
- 基本思想
- 具体代码
- 优化(埃氏算法)
- 基本思想(时间复杂度约为n)
- 具体代码
- 优化2(线性筛法)
- 基本思想
- 具体代码
- 约数
- 求一个数的所有约数
- 试除法
- 约数个数
- 基本思想
- 具体题目+代码
- 题目以及分析
- 代码
- 约数之和
- 基本思想
- 具体代码
- 求最大公约数
- 基本思想(欧几里得算法)
- 具体代码
质数(素数)
定义

判断是否为质数
暴力写法,试除法
基本思想
从定义出发,判断是否为质数
1、小于2的数,统一返回false
2、遍历 i 从2到小于n(即除去1和n)
判断是否有n % i == 0 的,表示这中间有i可以整除,如果有,返回false
最后返回true
具体写法
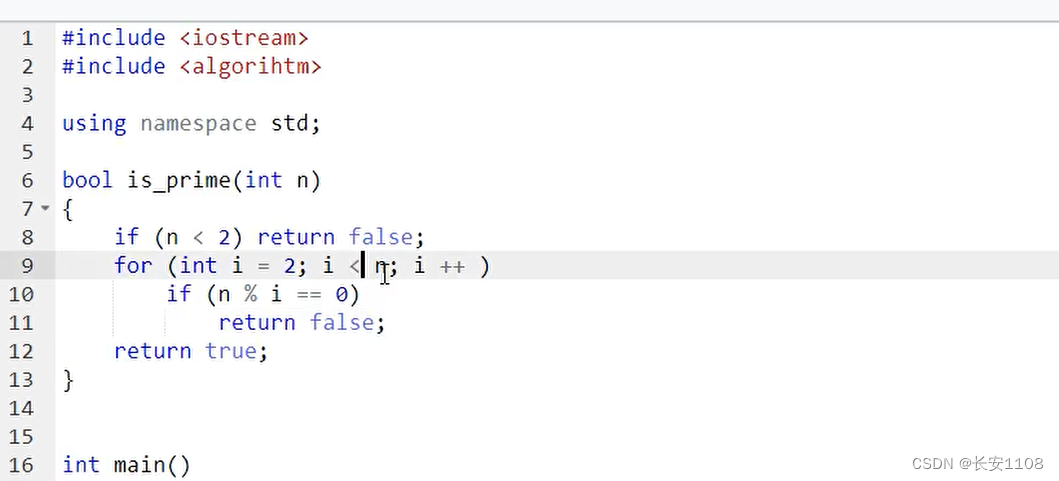
优化
基本思想(时间复杂度根号n)
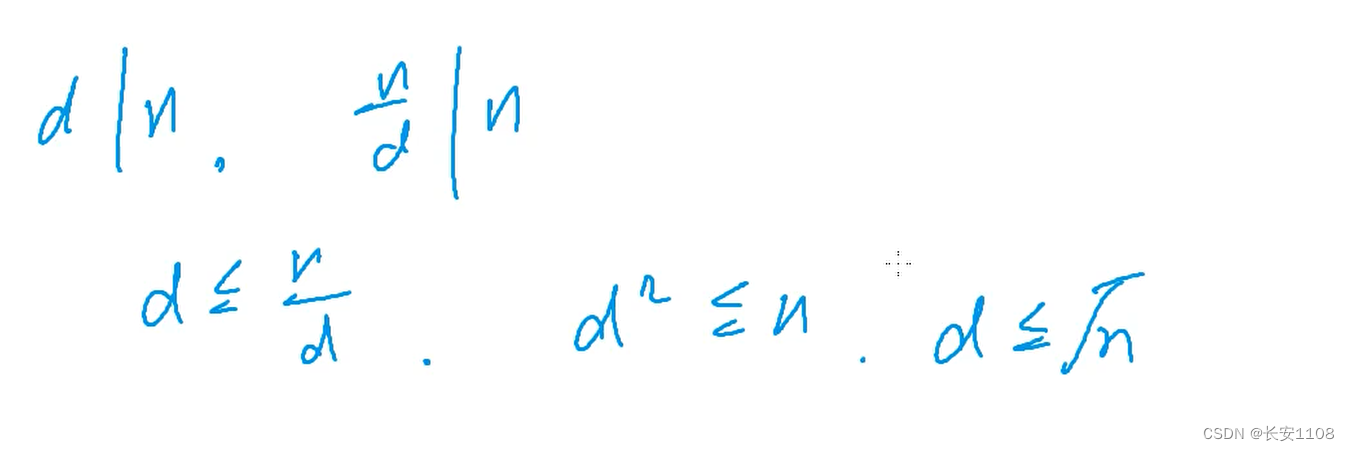
利用质数的性质,当d能被n整除时,n/d 也能被n整除,
所以,只需要判断从2到根号n有无能让d整除的数即可
具体写法
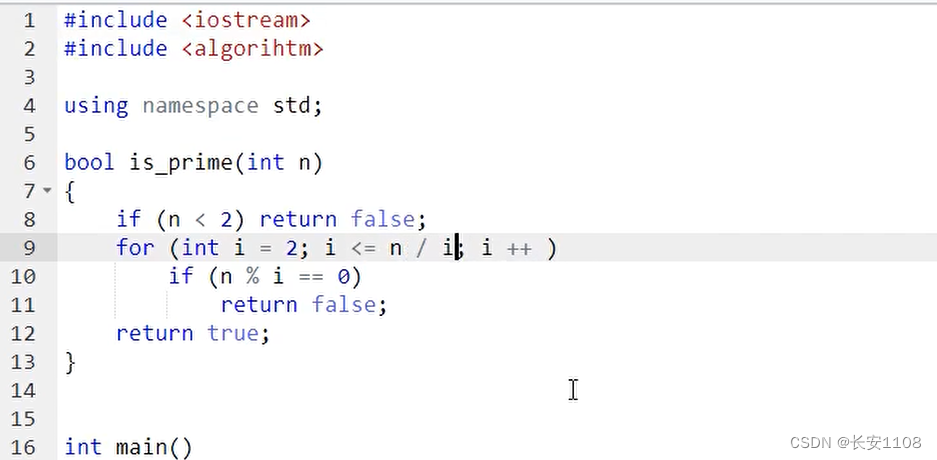
这里的 i 就是上面的d,循环 i 判断是否有数能让n整除,也就是上面的判断d是否能让n整除
分解质因数
分析题意

质因子分解,就是输出几组质数并输出他们对应的数量,他们乘积等于输入的数
暴力写法
基本思想
直接循环所有从2到等于n的数,如果能找到一个被n整除的 i ,那么 i 一定是一个质数,这里与上面判断质数的代码要区分开,
上面写到:
for循环里,if(n % i == 0) return false
因为上面是判断n是否为质数,跟 i 没有关系
而本题的重点不在n,而是他的因子 i,所以这里当可以整除时, i 一定是一个质数,这句话就不会与上面矛盾了
具体代码

纠正:int x 改为 int n
循环i从2到小于等于n,其中如果找到了一个i能被n整除,那么这个i一定是质数,他就是我们要找的质因子之一(具体原因见上方“基本思想”),之后循环计算 i 的次数即可
循环计算质数次数时:
首先定义一个计数器s=0;
之后,while循环,条件是n 还可以整除 i
条件成立,就更新n 为 n/i,(因为题设是多个质因子的乘积,所以要进行下一步判断的话,要先将已经判断出来的 i 除去)
之后计数器++
输出质子以及出现的次数
优化
基本思想(时间复杂度小于等于根号n)

利用性质:n中最多只包含一个大于根号n的质因子
证明:如果有两个大于跟好n的质因子,那么这两个相乘,一定大于n,不成立,所以该性质成立,我们可以利用这个性质进行优化
具体代码

将for循环的 i ,从2开始循环到 小于等于n/i
然后,其他的不变,在for循环结束之后,如果n>1(因为n在上面的过程中,不断的被除开,不断的变小,被除开的原因见上面“未优化时具体代码的解释”),那么这个n就是那个大于根号n的质因子,他的个数永远为1,因为只存在一个大于根号n的质因子
tip:puts(“”);可以输出一行回车
同时puts(“字符串”);可以输出字符串
筛质数(区别于判断质数,这个是筛选出来并保存,质数的数目较多)
基本思想
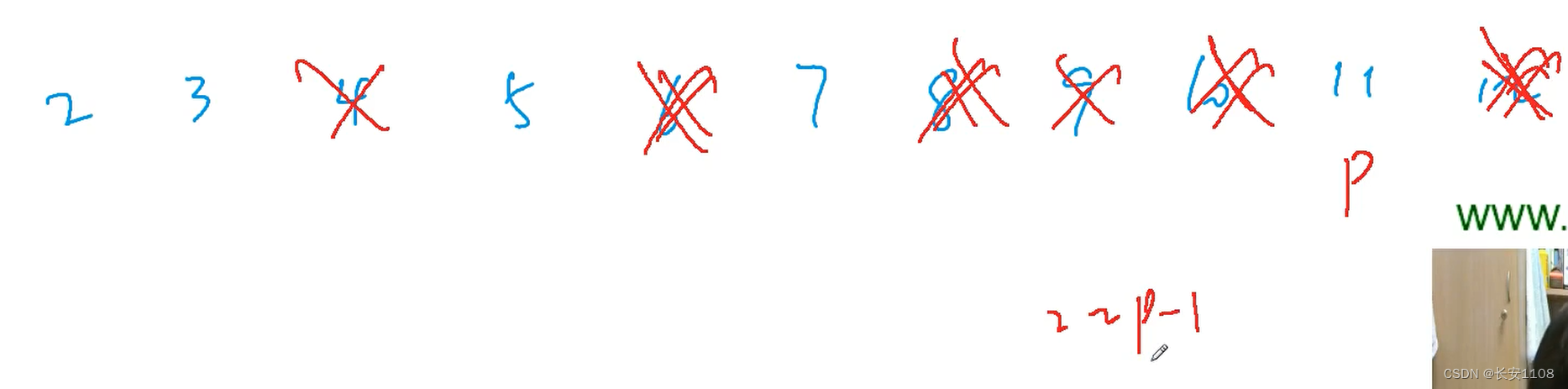
从2开始,删除后面2的倍数、删除3的倍数、4、5…
最后留下的都是质数,
因为假设p被留下了,那么就是前面2到p-1都没能把p删掉,也就是前面的倍数都没有p,所以p也就没有除去1和本身以外的因子,所以p一定是质数
具体代码
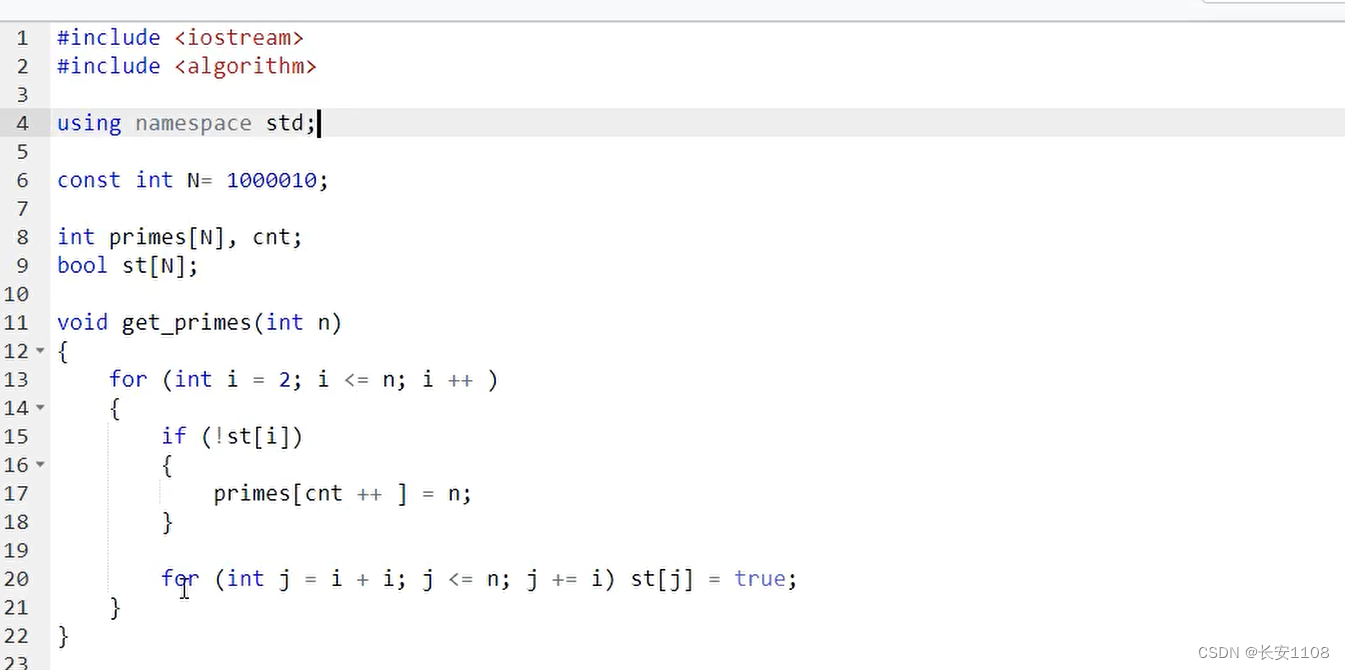
纠正:17行 primes【】= i
prime数组用来存放质数
cnt用来移动prime数组里的坐标,同时也在计数
st数组用来记录某个数是否被删掉了
首先从2到小于等于n遍历 i
之后 直接判断是否st[i]为假,如果是,那么放入prime数组中,并且cnt++
if之后,使用for循环对倍数进行删除:
初始化 j 为 i+i ; j <=n ; j += i
st[j]=true
初始化为 i 的2倍,之后递增条件是在 j 的基础上依次加 i,这样就可以找到 i 的所有倍数
优化(埃氏算法)
基本思想(时间复杂度约为n)
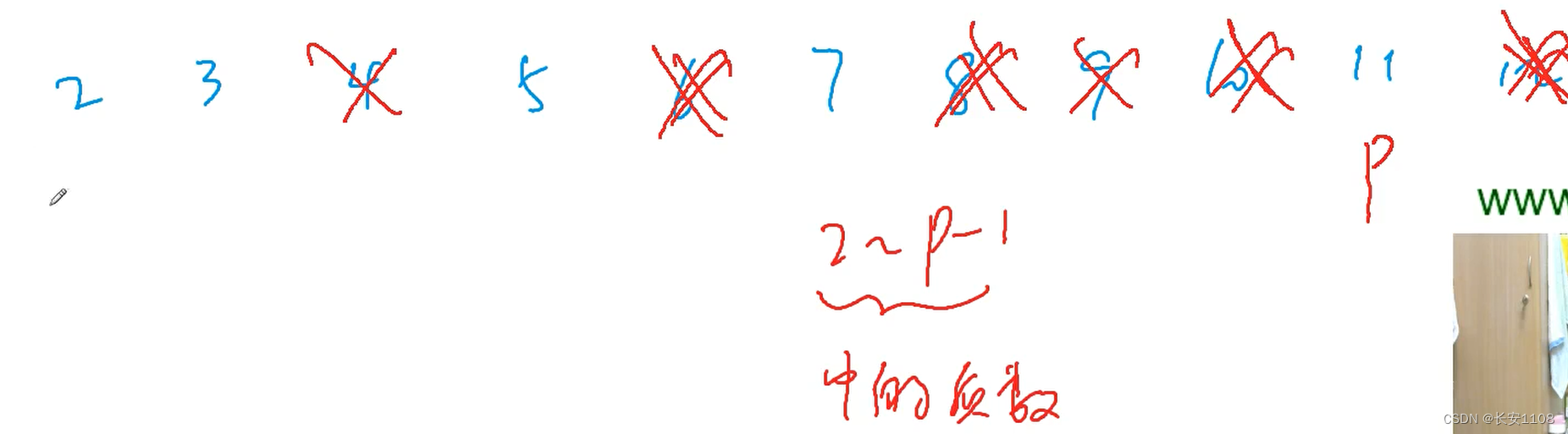
我们的目的是删掉合数,
任何一个合数都会被筛掉,因为质数的倍数包括所有的合数,任何一个合数都有一个质因子
所以我们只需要删除出来前面质数的倍数即可
具体代码

纠正:17行 primes【】= i
将for循环放入if里面即可
优化2(线性筛法)
基本思想

埃氏筛法:
我们的目的是删掉合数,
任何一个合数都会被筛掉,因为质数的倍数包括所有的合数,任何一个合数都有一个质因子
所以我们只需要删除出来前面质数的倍数即可
线性筛法的思路仍然是删掉质数的倍数 , 但是这种算法是根据每个最小质因子的倍数去筛,效率更高
具体代码
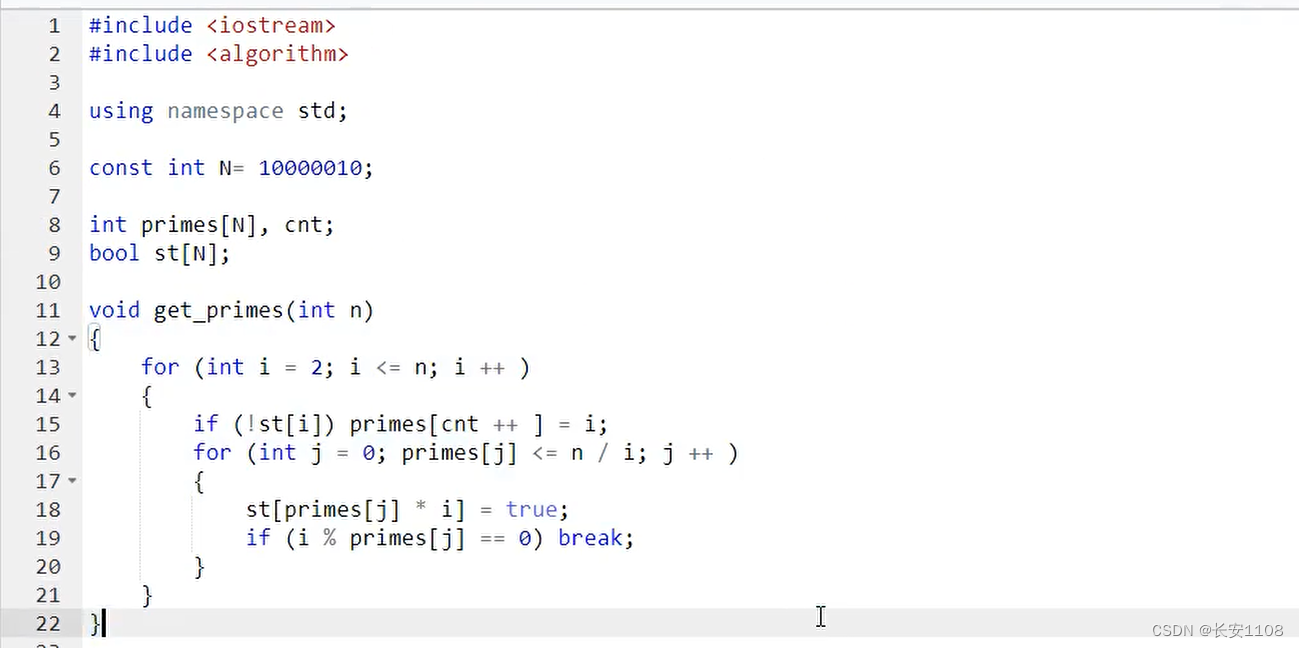
仍然是for循环 i 从2到小于等于 n
之后if不变
改变一下第二个for循环 :
j初始化为0 ;之后primes[j]<= n/i ;j++
然后标记st[primes[ j ] * i ]=true; (删除每个最小质因子的倍数)
之后加一个if (i % primes[ j ] == 0) break; (这一步可以保证primes[ j ]是 i 的最小质因子)
注意点:关于筛质数的三个算法中,只有该算法的第二个for循环不同于其他两个,前两个的第二个for循环都一样,只是位置不同,要特别注意
约数
求一个数的所有约数
试除法
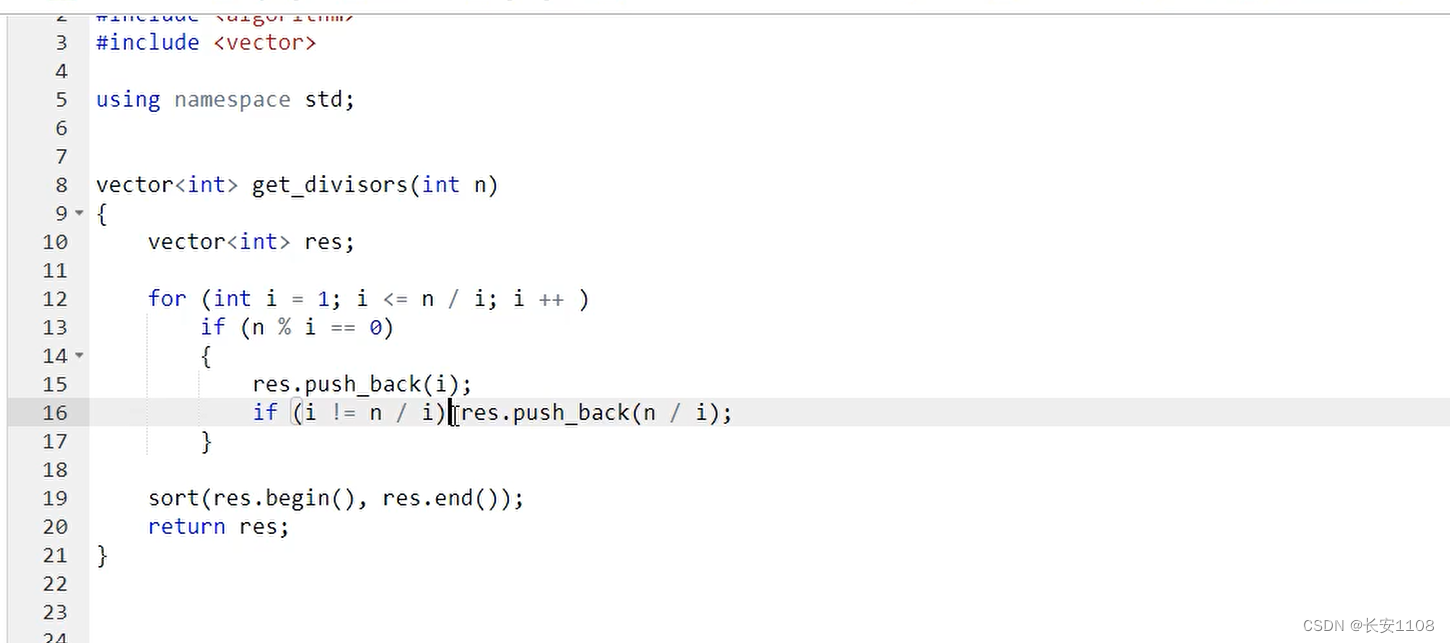
注意返回值是一个vector容器
首先是for循环从1到小于等于n
if i能被n整除
那么这个i就是一个约数,加入到容器中
另外这里需要一个特判:如果 i != n / i ,就把n / i 加到容器中,(因为约数不同于质数,约数是成对出现的,当我们找到一个 i 之后,可以顺势将其成对的另一个也加入到容器,前提是 i != n / i ,保证是两个成对的约数不相同时才加进去)
约数个数
基本思想
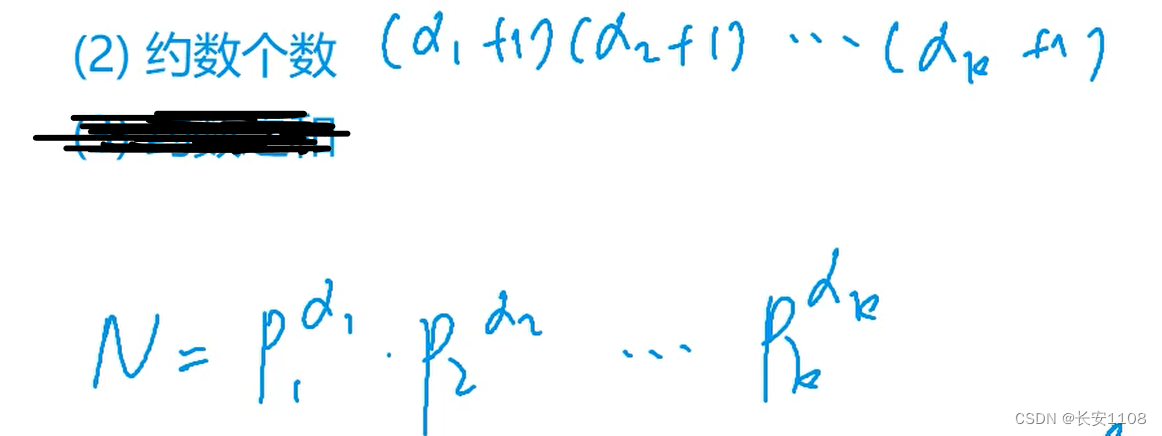
对于一个数N,可以写成多项的多次相乘的形式,这样的话,约数个数就是各个指数各自加一之后相乘的结果
原因:因为约数也就是N的因子,当N写成上图这种形式的时候,随便去掉一个p的一个次幂,相当于提出来了一个p的一次,而剩下的部分,还是N的因子,也还是N的约数,而a1次方的话,有0到a1一共(a1+1)种提法,所以所有的提法排列组合的个数,就是约数的个数
具体题目+代码
题目以及分析
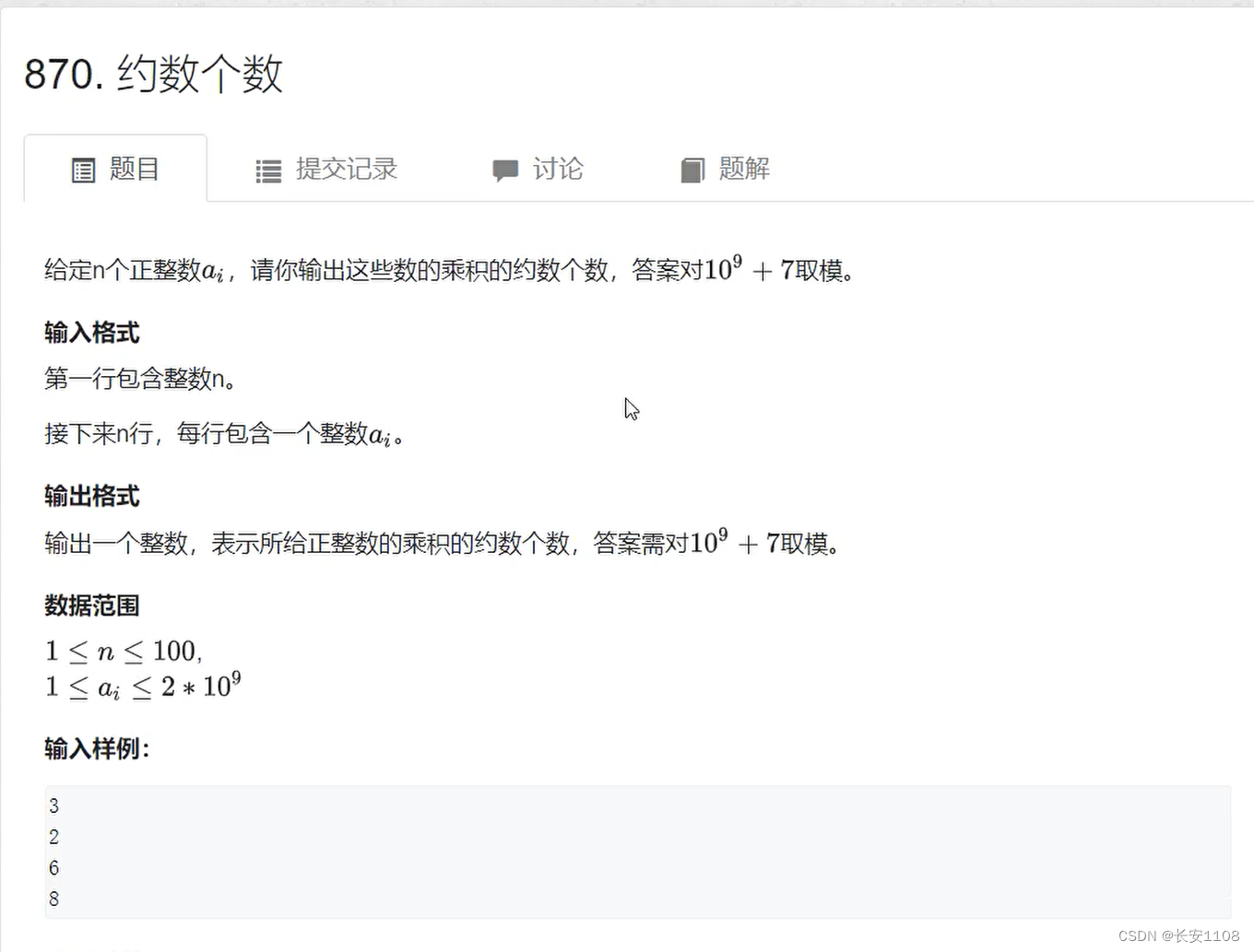
该题是一个n个整数乘积的原始数,所以,我们在求这个数的约数个数时,要先将乘积得到的结构进行分解,分解成指数相乘形式,具体我们可以先对每一个数进行分解,每个数分解出来指数形式之后,存入一个map里,这样依次进行下去,就可以得到一个个的底数和次幂组合,拿到这些组合,就可以计算约数个数或者约数之和
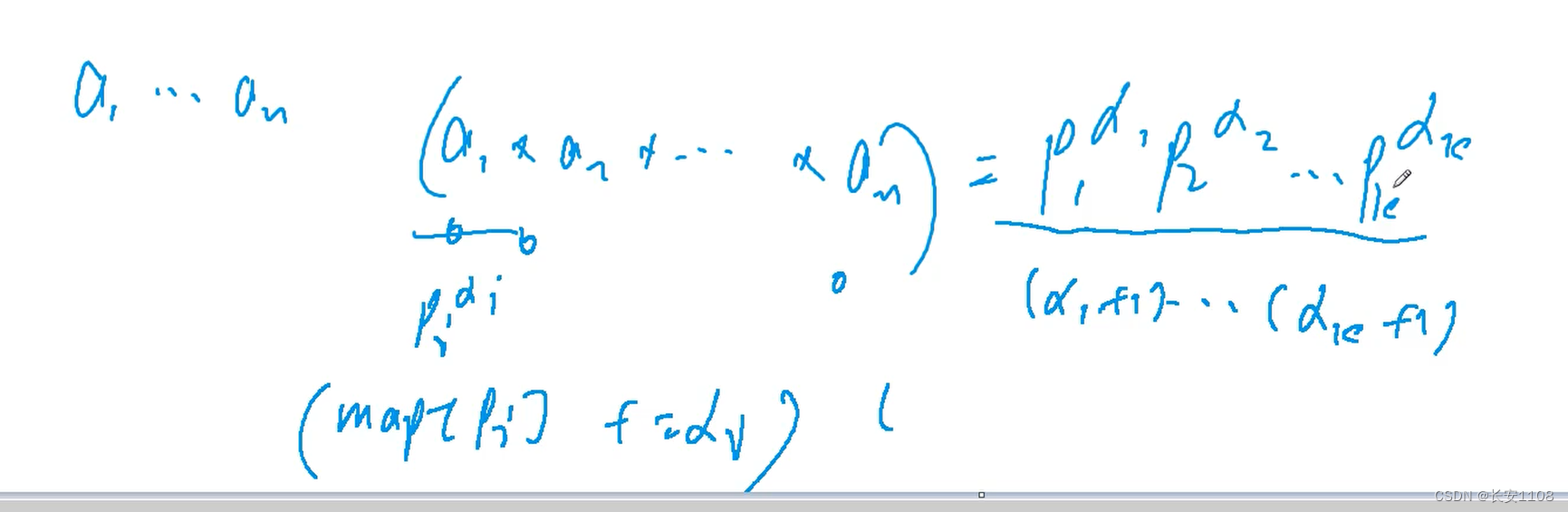
代码
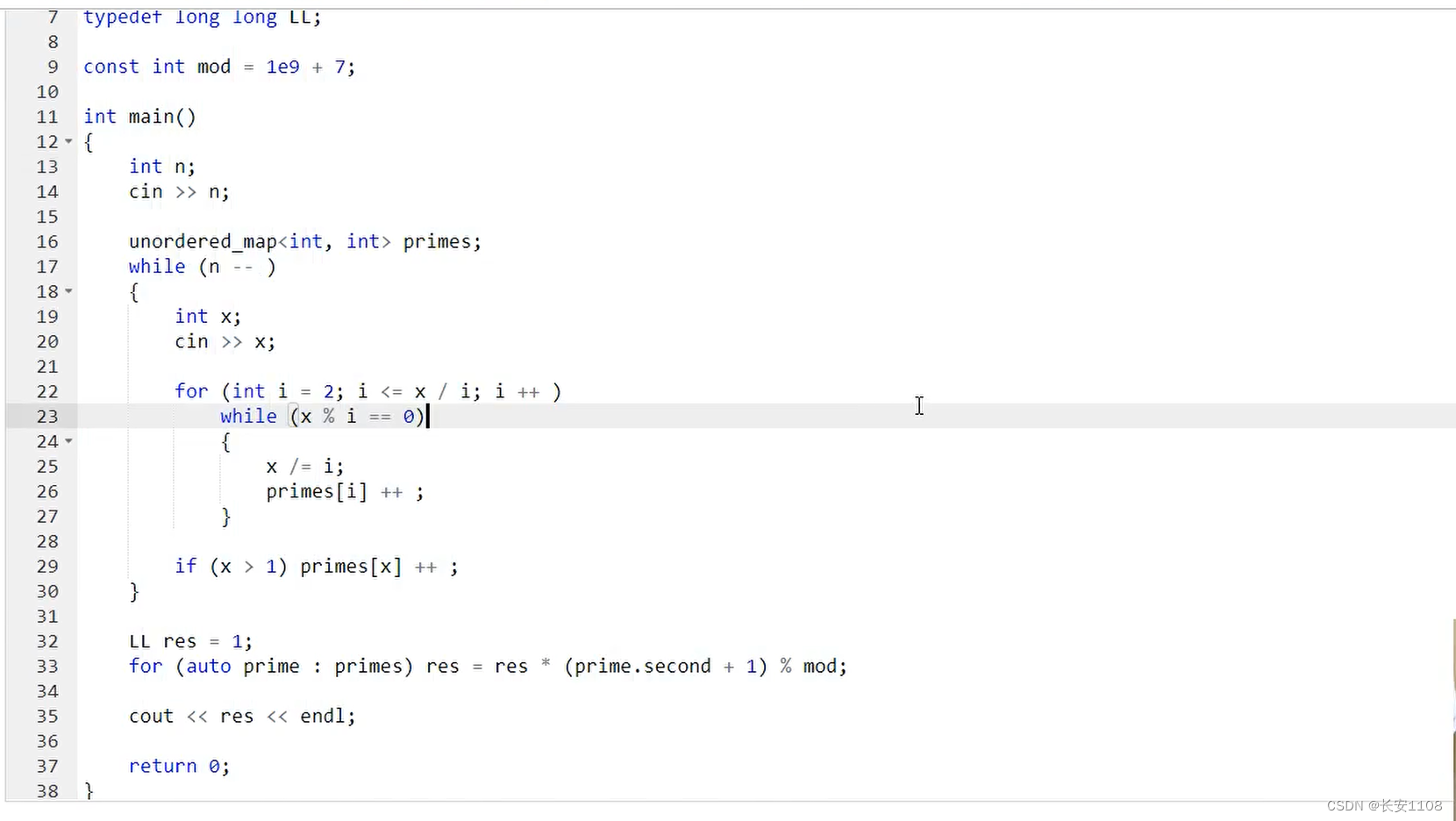
首先,操作的目标放在每一个输入进来的数,依次对其进行分解,分解的方式采用质因子分解:(实际上与上面的质因子分解如出一辙):
对于n个循环,每输入一个x,
我们对其进行一个for循环,i 从2到 小于等于 x / i
for循环里while循环,如果有x % i ==0
更新x(去除掉 i 部分)
同时primes[ i ] ++,i 的map值就是以 i 为底的组合中的次幂部分
for循环之后,就是对那个大于根号x的质子的特判,将其加入到primes的map中
之后就是根据题设套不同的公式,这里是求约数的个数,带入约数的个数公式即可,如上图
tips:

typedef long long LL;
数据范围巨大的数会用到LL
10的9次方+7,表示为: 1e9+7
约数之和
基本思想
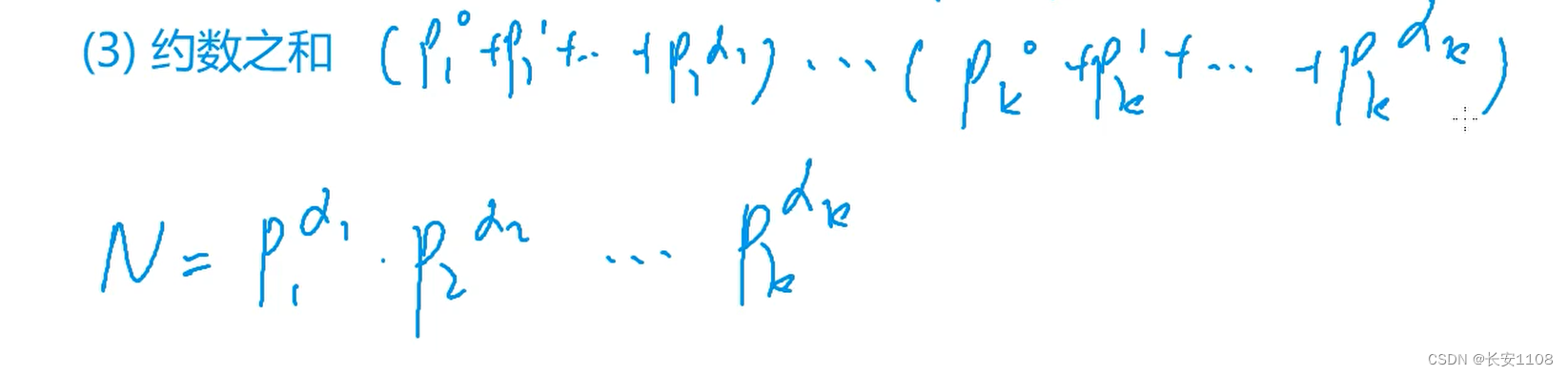
具体代码
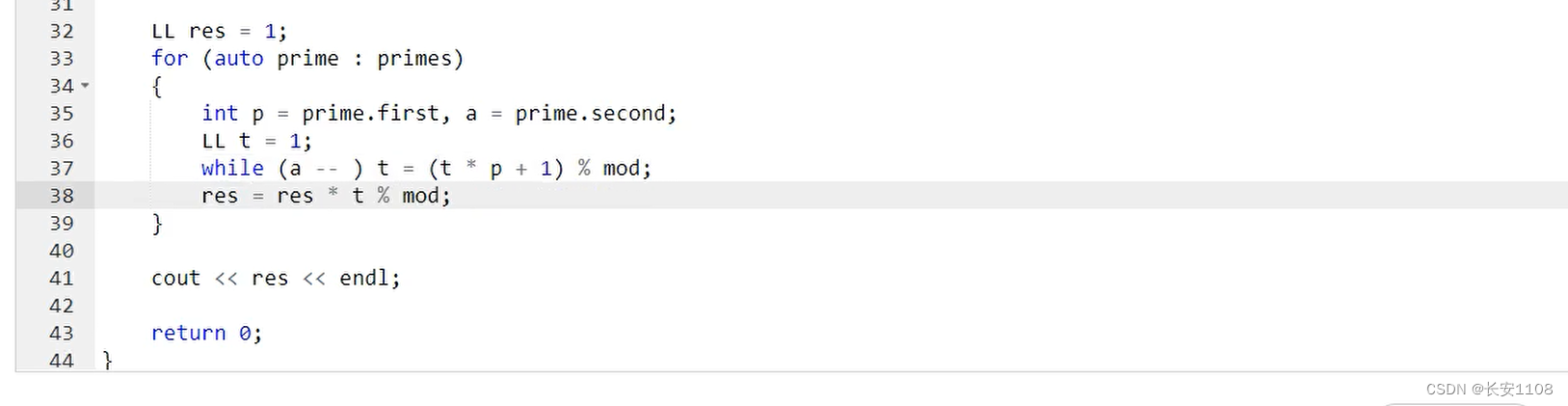
核心代码与上面的一样,不同的是公式的计算
for循环里面使用迭代器
对于每一个prime,先取出来first 以及 second
然后计算出他的p的0+p的1+p的2+p的3+…:
while(a–)t = (t * p +1),这样的话就可以得到p的0+p的1+p的2+p的3+…,上图取mod,是为了在这里取一次,可以节省效率
之后将while得到的t,乘入res,并取模,即可
具体while中的公式效果见下图:

求最大公约数
基本思想(欧几里得算法)

重要的是上图第二行被框住的部分
a 和 b 的最大公约数,可以转化为求b 和 a mod b 的最大公约数
具体代码
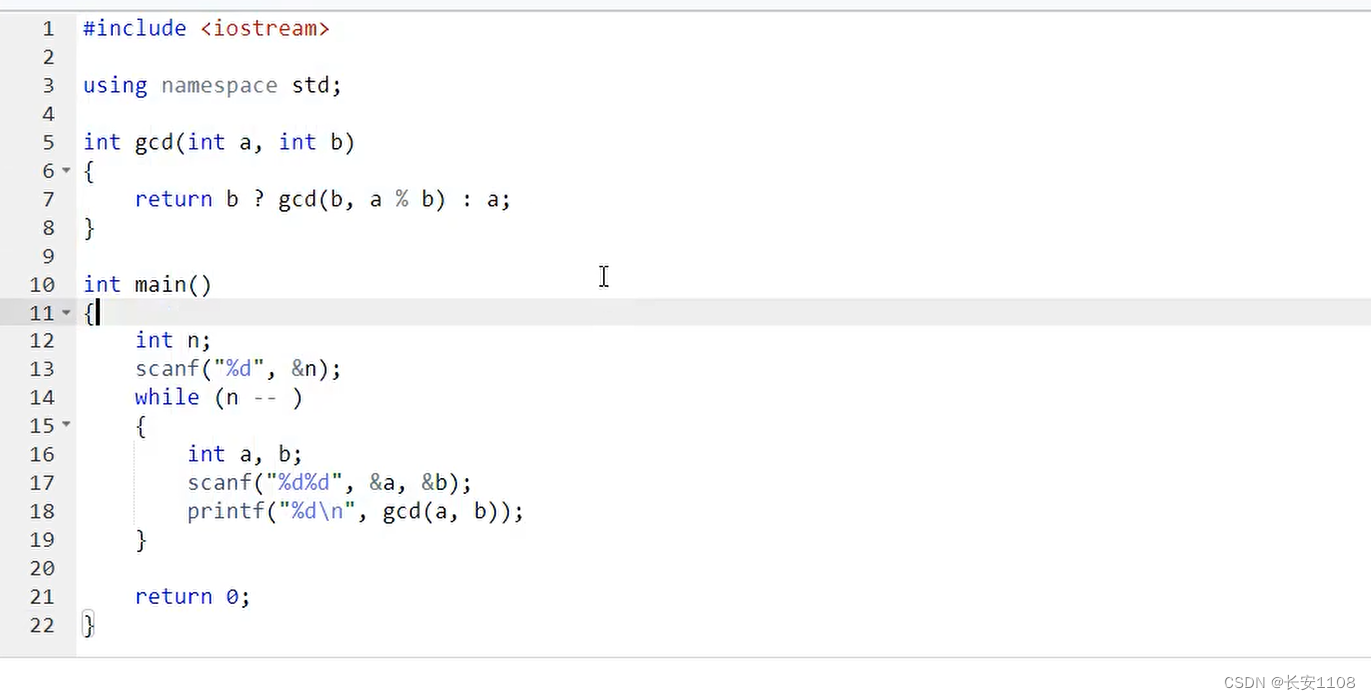
一行的模版
直接返回 b ?gcd(b, a % b ) : a
当b不为0时,返回gcd(b , a % b),递归下去
当b等于0,返回a即可