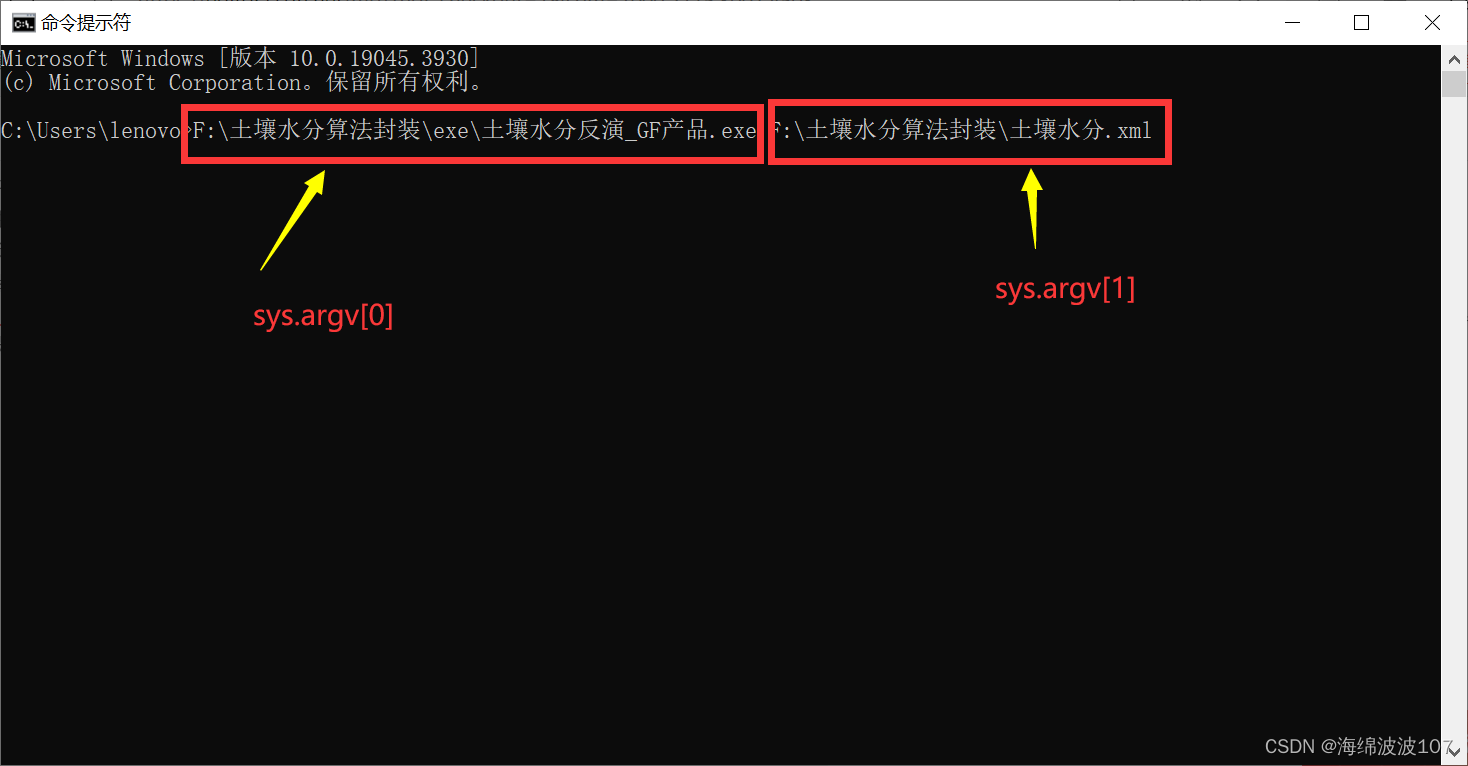
题目：

我们有一堆数，找出模Y的最小值。

思路：

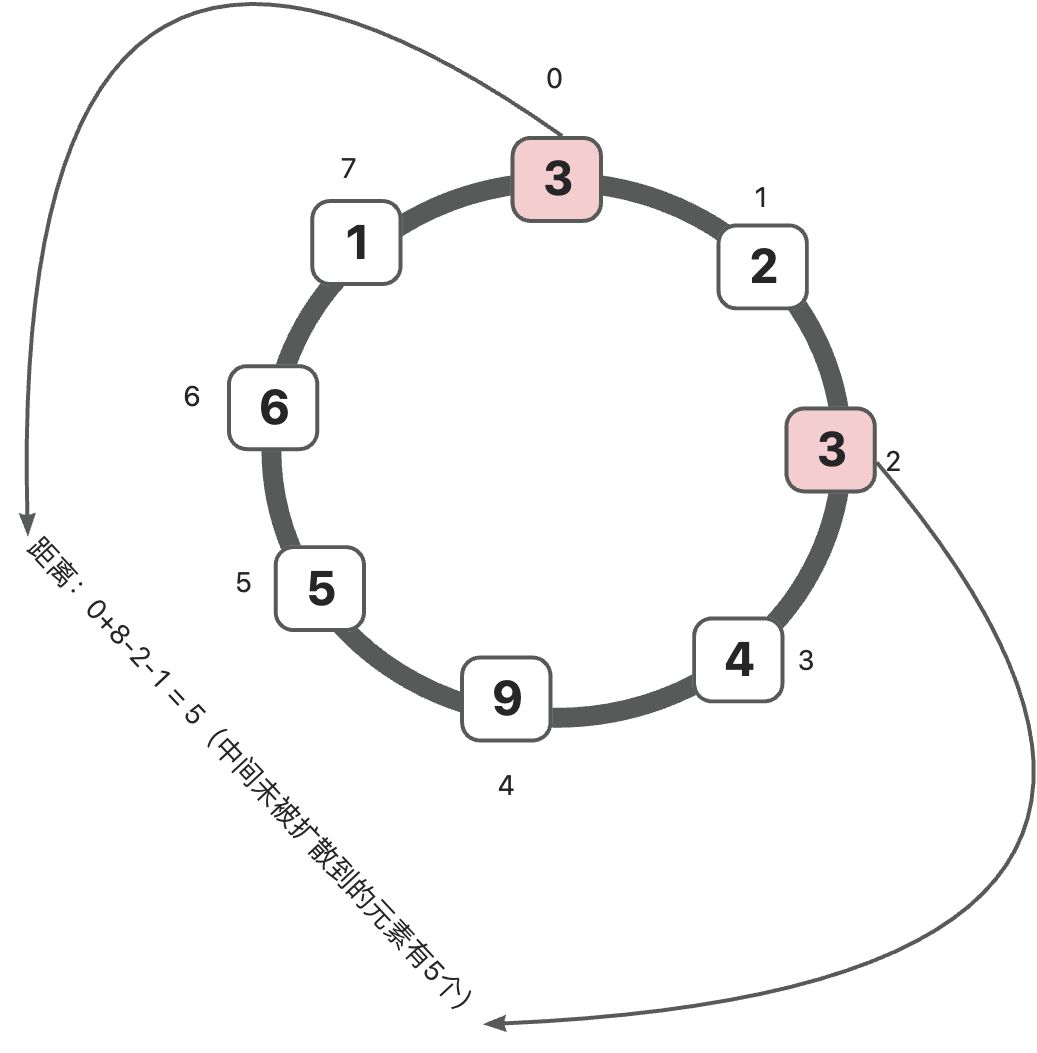
我们初步思考，会发现每个Y是一段，比如 1~Y , Y~2Y , 2Y~3Y ...

每个区间都可能有最小的答案。

这里对Y可以使用根号分治，因为：

当Y足够大时，每个区间都很大，区间数就很少。

而当Y足够小时，我们可以暴力这部分Y。

当Y足够大时，区间很大，我们对区间做处理：找大于1的最小值，大于Y的最小值，大于2Y的最小值，只需要找几次就能找完。

————

暂时规定Y小于V时，Y足够小。

A操作：

我们每插入一个数，挨着取模1~V并记录对应的最小值。（这里就是暴力，只记录1~V是可以承受的）

这样取模1~V的时候我们直接得到最小值。可以用map存。

（同时插入的数存入一个set中。）

B操作：

当模数小于V时，我们已经存好了，直接得到答案。

当模数大于V时，我们在每个区间找最小值。(因为区间很大，过几个区间可能就没有数了，结束就好了)

根号：

V怎么取呢？这。。

根号分治！

本题 Y ≤ 3e5，取个几百差不多，V*B == 3e5就行。（这个B对应大区间数目，大区间最小是V的时候也要覆盖整个Y，所以有个B）

可以取 ： 480*625        近似根号了，因为我们区间长度是整数

代码细节：

可以直接看代码，也可以看这里帮助理解写法：

set存数，lower_bound是下界的意思（参考set::lower_bound - C++ Reference (cplusplus.com)）

（可以测试lower_bound，当找的那个下界x不存在时，返回的是第一个比x大的数的迭代器

而up_bound找的就是第一个比x大的数的迭代器。这里我们要找最小的大于等于区间左边的数）

代码：

#define V 480
#define B 625

void solve()
{
	int n;
	cin >> n;
	set<int>s;
	unordered_map<int, int>m;
	for (int i = 1; i <= n; i++)
	{
		char op;
		int val;
		cin >> op >> val;
		if (op == 'A')
		{
			s.insert(val);
			for (int i = 1; i < V; i++)
			{
				if (m.count(i))m[i] = min(m[i], val % i);
				else m[i] = val % i;
			}
		}
		else
		{
			int ans = LLONG_MAX;
			if (val >= V)
			{
				for (int i = 0; i <= B; i++)
				{
					auto it = s.lower_bound(i * val);
					if (it == s.end())
						break;//都比i*val大了
					ans = min(ans, *it - (i * val));
				}
			}
			else
			{
				ans = m[val];
			}
			cout << ans << endl;
		}

	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int t = 1;
	//cin >> t;
	while (t--)
	{
		solve();
	}
	return 0;
}

然而。。。：

值域分块可以再优化，我不会。

我导师的讲解：