代码随想录算法训练营29期|day37 任务以及具体任务

第八章贪心算法 part06

738.单调递增的数字

版本2
class Solution {
    public int monotoneIncreasingDigits(int n) {
        String s = String.valueOf(n);
        char[] chars = s.toCharArray();
        int start = s.length();
        for (int i = s.length() - 2; i >= 0; i--) {
            if (chars[i] > chars[i + 1]) {
                chars[i]--;
                start = i+1;
            }
        }
        for (int i = start; i < s.length(); i++) {
            chars[i] = '9';
        }
        return Integer.parseInt(String.valueOf(chars));
    }
}

思路：每遇到一个前面的数大于后面的情况，就把前面的数-1，然后把后面的所有数赋值为9，达成最大的目的，用start记录需要修改的位置，切记！！start要赋值为s的长度。

968.监控二叉树

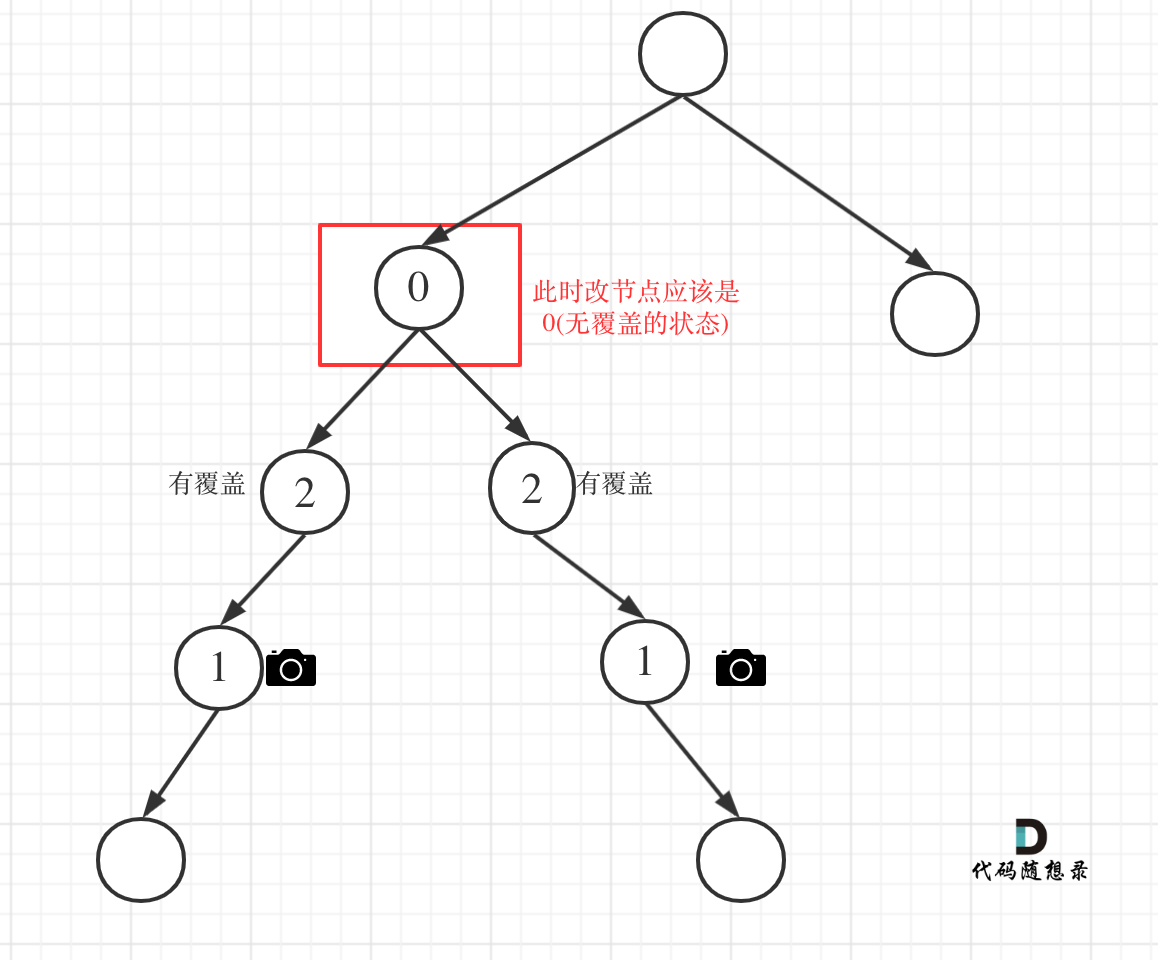
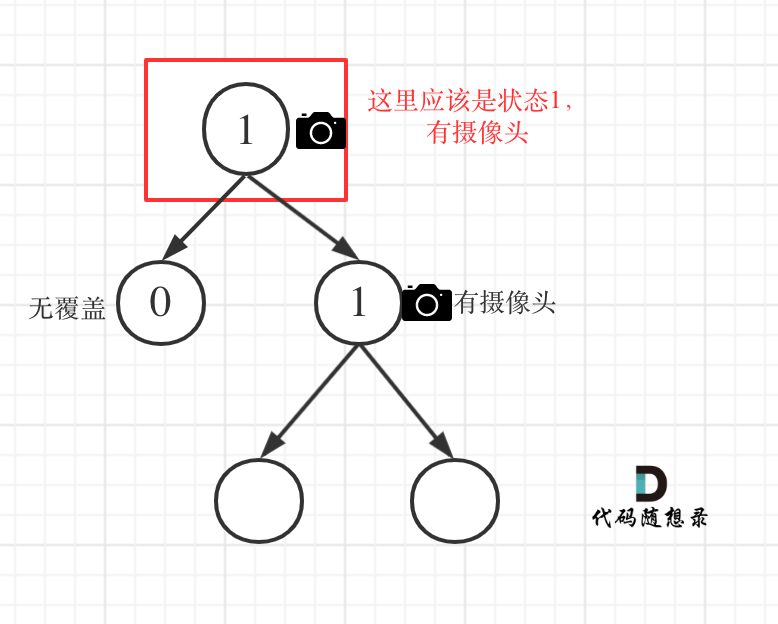
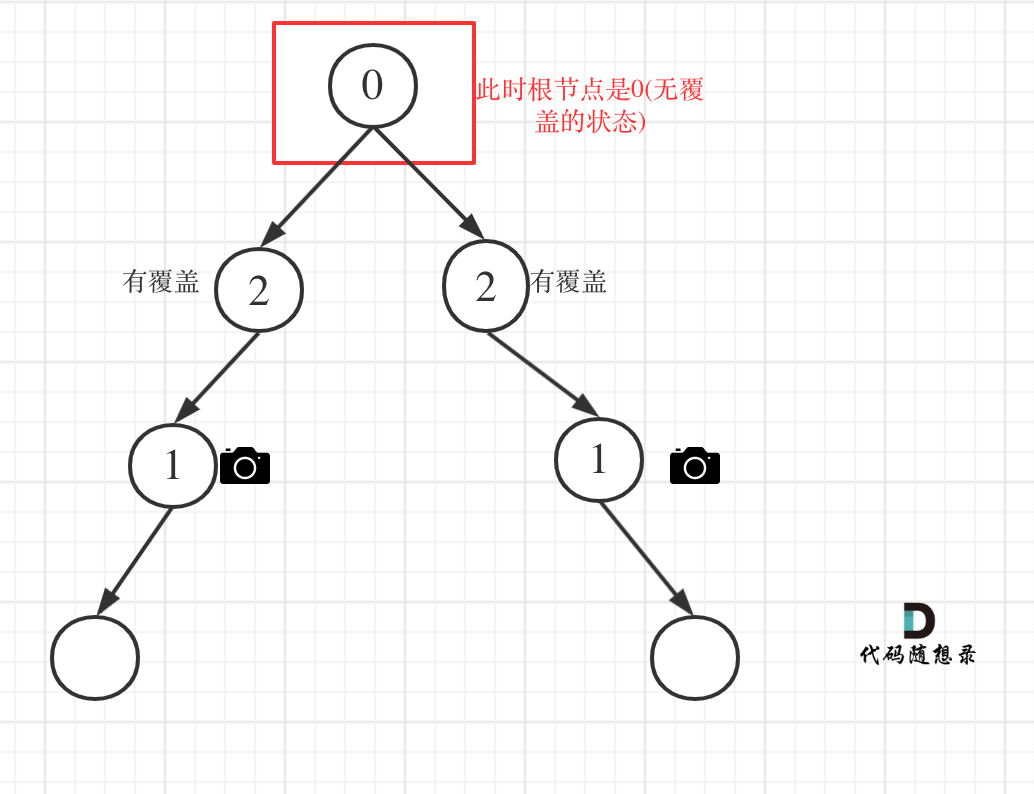
class Solution {
    int  res=0;
    public int minCameraCover(TreeNode root) {
        // 对根节点的状态做检验,防止根节点是无覆盖状态 .
        if(minCame(root)==0){
            res++;
        }
        return res;
    }
    /**
     节点的状态值：
       0 表示无覆盖
       1 表示 有摄像头
       2 表示有覆盖
    后序遍历，根据左右节点的情况,来判读 自己的状态
     */
    public int minCame(TreeNode root){
        if(root==null){
            // 空节点默认为 有覆盖状态，避免在叶子节点上放摄像头
            return 2;
        }
        int left=minCame(root.left);
        int  right=minCame(root.right);

        // 如果左右节点都覆盖了的话, 那么本节点的状态就应该是无覆盖,没有摄像头
        if(left==2&&right==2){
            //(2,2)
            return 0;
        }else if(left==0||right==0){
            // 左右节点都是无覆盖状态,那 根节点此时应该放一个摄像头
            // (0,0) (0,1) (0,2) (1,0) (2,0)
            // 状态值为 1 摄像头数 ++;
            res++;
            return 1;
        }else{
            // 左右节点的 状态为 (1,1) (1,2) (2,1) 也就是左右节点至少存在 1个摄像头，
            // 那么本节点就是处于被覆盖状态
            return 2;
        }
    }
}

思路：该题较为复杂，是二叉树和贪心的结合，分为三种状态0：无覆盖 1：代表摄像头 2：代表覆盖，还得处理三种不同的情况，左右子树全覆盖，返回0无覆盖；左或者右子树为无覆盖，父节点为摄像头1；左或者右子树为摄像头，父节点为2覆盖，注意！！处理逻辑二和三不能颠倒顺序。

968.监控二叉树2

贪心算法总结篇

我刚刚开始讲解贪心系列的时候就说了，贪心系列并不打算严格的从简单到困难这么个顺序来讲解。

因为贪心的简单题可能往往过于简单甚至感觉不到贪心，如果我连续几天讲解简单的贪心，估计录友们一定会不耐烦了，会感觉贪心有啥好学的。

但贪心的难题又真的有点难，所以我是简单困难交错着讲的，这样大家就感觉难度适中，而且贪心也没有什么框架和套路，所以对刷题顺序要求没有那么高。

但在贪心系列，我发的题目难度会整体呈现一个阶梯状上升，细心的录友们应该有所体会。

在刚刚讲过的回溯系列中，大家可以发现我是严格按照框架难度顺序循序渐进讲解的，和贪心又不一样，因为回溯法如果题目顺序没选好，刷题效果会非常差！

同样回溯系列也不允许简单困难交替着来，因为前后题目都是有因果关系的，相信跟着刷过回溯系列的录友们都会明白我的良苦用心。

每个系列都有每个系列的特点，我都会根据特点有所调整，大家看我每天的推送的题目，都不是随便找一个到就推送的，都是先有整体规划，然后反复斟酌具体题目的结果。

那么在贪心总结篇里，我按难易程度以及题目类型大体归个类。

贪心大总结正式开始：

#贪心理论基础

在贪心系列开篇词关于贪心算法，你该了解这些！ (opens new window)中，我们就讲解了大家对贪心的普遍疑惑。
贪心很简单，就是常识？
跟着一起刷题的录友们就会发现，贪心思路往往很巧妙，并不简单。
贪心有没有固定的套路？
贪心无套路，也没有框架之类的，需要多看多练培养感觉才能想到贪心的思路。
究竟什么题目是贪心呢？
Carl个人认为：如果找出局部最优并可以推出全局最优，就是贪心，如果局部最优都没找出来，就不是贪心，可能是单纯的模拟。（并不是权威解读，一家之辞哈）

但我们也不用过于强调什么题目是贪心，什么不是贪心，那就太学术了，毕竟学会解题就行了。
如何知道局部最优推出全局最优，有数学证明么？
在做贪心题的过程中，如果再来一个数据证明，其实没有必要，手动模拟一下，如果找不出反例，就试试贪心。面试中，代码写出来跑过测试用例即可，或者自己能自圆其说理由就行了

就像是要用一下 1 + 1 = 2，没有必要再证明一下 1 + 1 究竟为什么等于 2。（例子极端了点，但是这个道理）

相信大家读完关于贪心算法，你该了解这些！ (opens new window)，就对贪心有了一个基本的认识了。

#贪心简单题

以下三道题目就是简单题，大家会发现贪心感觉就是常识。是的，如下三道题目，就是靠常识，但我都具体分析了局部最优是什么，全局最优是什么，贪心也要贪的有理有据！
贪心算法：分发饼干(opens new window)
贪心算法：K次取反后最大化的数组和(opens new window)
贪心算法：柠檬水找零(opens new window)
#贪心中等题

贪心中等题，靠常识可能就有点想不出来了。开始初现贪心算法的难度与巧妙之处。
贪心算法：摆动序列(opens new window)
贪心算法：单调递增的数字(opens new window)
#贪心解决股票问题

大家都知道股票系列问题是动规的专长，其实用贪心也可以解决，而且还不止就这两道题目，但这两道比较典型，我就拿来单独说一说
贪心算法：买卖股票的最佳时机II(opens new window)
贪心算法：买卖股票的最佳时机含手续费 (opens new window)本题使用贪心算法比较绕，建议后面学习动态规划章节的时候，理解动规就好
#两个维度权衡问题

在出现两个维度相互影响的情况时，两边一起考虑一定会顾此失彼，要先确定一个维度，再确定另一个一个维度。
贪心算法：分发糖果(opens new window)
贪心算法：根据身高重建队列(opens new window)
在讲解本题的过程中，还强调了编程语言的重要性，模拟插队的时候，使用C++中的list（链表）替代了vector(动态数组)，效率会高很多。

所以在贪心算法：根据身高重建队列（续集） (opens new window)详细讲解了，为什么用list（链表）更快！

大家也要掌握自己所用的编程语言，理解其内部实现机制，这样才能写出高效的算法！

#贪心难题

这里的题目如果没有接触过，其实是很难想到的，甚至接触过，也一时想不出来，所以题目不要做一遍，要多练！

#贪心解决区间问题

关于区间问题，大家应该印象深刻，有一周我们专门讲解的区间问题，各种覆盖各种去重。
贪心算法：跳跃游戏(opens new window)
贪心算法：跳跃游戏II(opens new window)
贪心算法：用最少数量的箭引爆气球(opens new window)
贪心算法：无重叠区间(opens new window)
贪心算法：划分字母区间(opens new window)
贪心算法：合并区间(opens new window)
#其他难题

贪心算法：最大子序和 (opens new window)其实是动态规划的题目，但贪心性能更优，很多同学也是第一次发现贪心能比动规更优的题目。

贪心算法：加油站 (opens new window)可能以为是一道模拟题，但就算模拟其实也不简单，需要把while用的很娴熟。但其实是可以使用贪心给时间复杂度降低一个数量级。

最后贪心系列压轴题目贪心算法：我要监控二叉树！ (opens new window)，不仅贪心的思路不好想，而且需要对二叉树的操作特别娴熟，这就是典型的交叉类难题了。

#贪心每周总结

周总结里会对每周的题目中大家的疑问、相关难点或者笔误之类的进行复盘和总结。

如果大家发现文章哪里有问题，那么在周总结里或者文章评论区一定进行了修正，保证不会因为我的笔误或者理解问题而误导大家。

所以周总结一定要看！
本周小结！（贪心算法系列一）(opens new window)
本周小结！（贪心算法系列二）(opens new window)
本周小结！（贪心算法系列三）(opens new window)
本周小结！（贪心算法系列四）(opens new window)
#总结

贪心专题汇聚为一张图：

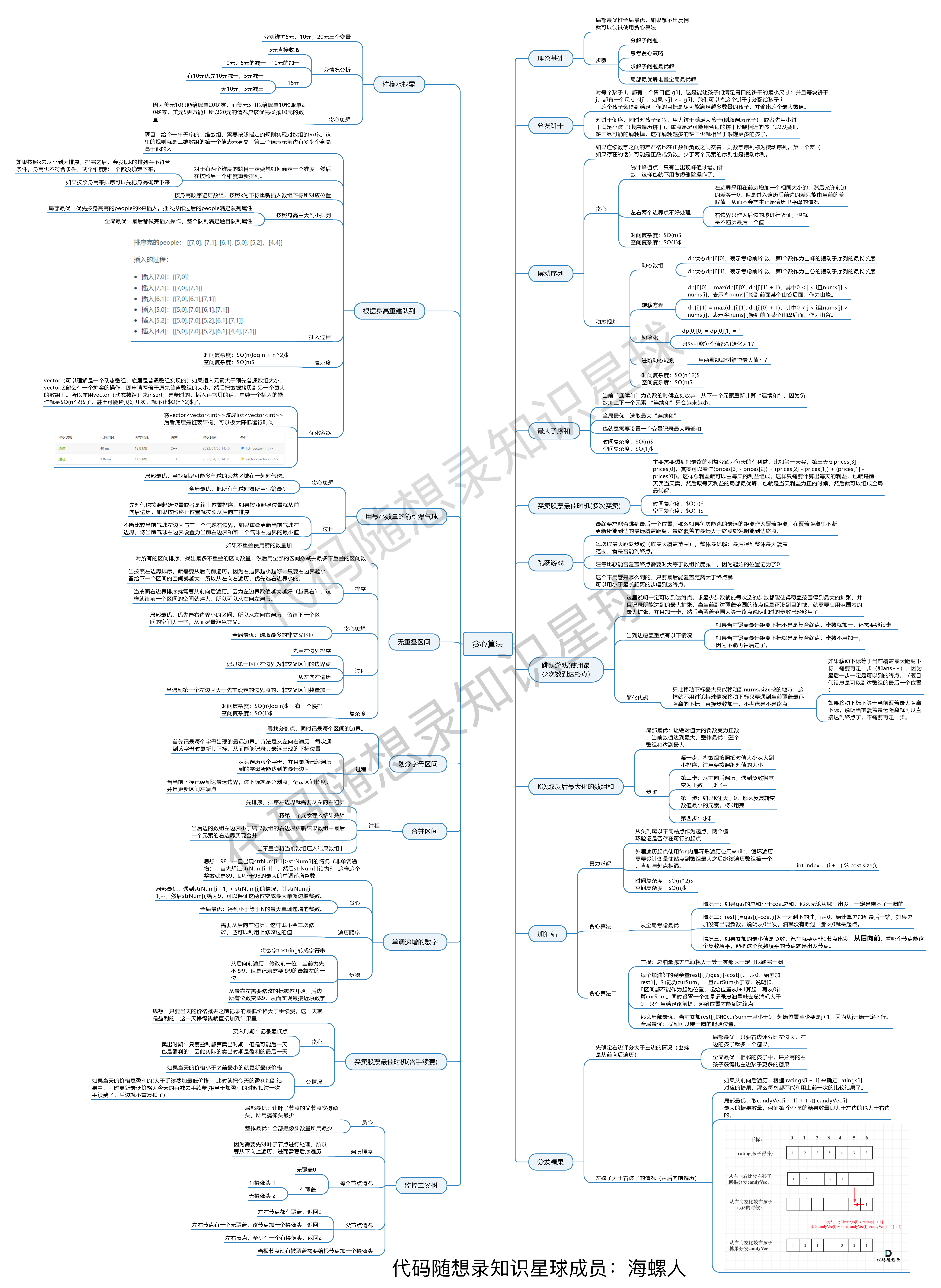
这个图是代码随想录知识星球 (opens new window)成员：海螺人 (opens new window)所画，总结的非常好，分享给大家。

很多没有接触过贪心的同学都会感觉贪心有啥可学的，但只要跟着「代码随想录」坚持下来之后，就会发现，贪心是一种很重要的算法思维而且并不简单，贪心往往妙的出其不意，触不及防！

回想一下我们刚刚开始讲解贪心的时候，大家会发现自己在坚持中进步了很多！

这也是「代码随想录」的初衷，只要一路坚持下来，不仅基础扎实，而且进步也是飞速的。

在这十八道贪心经典题目中，大家可以发现在每一道题目的讲解中，我都是把什么是局部最优，和什么是全局最优说清楚。