8位有符号整数-128的二进制码是1000 0000,而+128的二进制码也是1000 0000,你是不是觉得很奇怪?
下面就让我来解释一下。
从-128到127的跨越
8位二进制数能够表示2^8共256个不同的值,从0000 0000到1111 1111。在8位有符号整数的世界,它的取值范围从-128到+127,其中负数128个,正数(包括0)128个,负数是-1到-128,因为有0的存在,所以正数是0到127。
在一个8位有符号整数系统中,最大能表示的正数是+127(0111 1111),因为最高位(即最左边的位)被用作符号位,0表示正数,1表示负数。
因此,128实际上不能用一个8位有符号整数直接表示。128的16位二进制表示是0000 0000 1000 0000,这里,最高位是0,表示它是正数。
二进制如何表示负数呢?
二进制表示正负数时,一般会把最高位当做符号位,符号位0表示正数,1表示负数,那么-1用二进制怎么表示呢?1用二进制表示为00000001,所以推算一下-1应该就是10000001吧?让我们来验证一下,看看对不对,十进制 1 +(-1)= 0,二进制 00000001 + 10000001 = 10000010 很明显不等于0 啊。
我们知道二进制1是00000001,那么我们倒推一下,00000001加上什么数会等于00000000呢?
想来想去都想不到啊,不知道你有没有发现,计算机是没有减法运算的,计算机的减法是通过加法实现的,那么加法怎么能达到减法的效果呢?
我们看下这个例子:
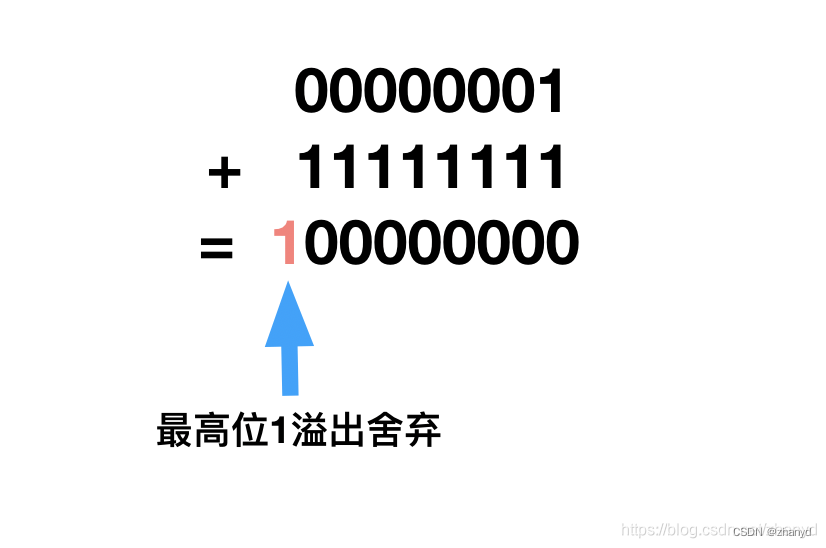
1 00000000超出了一个字节的范围,最高位1被舍弃,剩下的就是 00000000,这就是十进制的0啊,推理可得-1用二进制表示就是11111111,好神奇,原来二进制的负数表示叫做补码,补码的转换规则是正数的取反再加1。
比如:00000001 取反就是 11111110,然后再加1就是11111111,这就是-1的二进制表示了。
仔细想想所谓补码,就是加起来等于11111111的码啊,然后再加1,最高位溢出后,不就等于0了吗,一个和原来的数加起来等于0的数不就是它的负数吗?
这么想是不是就容易理解了呢?
如果你想了解计算机如何计算减法的,可以看下这篇文章:
计算机只会加法,那么它如何用加法来计算减法呢?
-128的独特之处
在8位有符号整数的范围内,-128占据了一个独特的位置。它不能通过常规的取反加1操作来得到,因为这样会超出8位的限制。因此,-128直接用1000 0000来表示,这在补码表示法中是一个例外。尽管这个表示也可以理解为+128的形式,但在8位有符号整数系统中,它被唯一地识别为-128。
如果把第一个数看成符号位的话1000 0000转换成十进制就是-0,但是-0没有意义,所以就拿来表示-128了。
验证
我们来验证一下,如果我们尝试将-128转换回正数,我们会先减1,得到0111 1111,然后取反,得到1000 0000,这代表正数128。所以,这验证了-128的二进制补码表示确实是1000 0000。
最后,我们再来看下8位有符号整数和16位有符号整数中-128的表示方法。
8位有符号整数
- 128:在8位有符号整数中,128实际上是无法表示的,因为8位有符号整数的取值范围是-128到127。如果我们试图表示128,它会超出这个范围。
- -128:在8位有符号整数中,-128是一个特殊情况,其二进制表示是1000 0000。这里,最高位(1)表示它是负数,其余位(000 0000)与128的正数表示相似,但在8位有符号系统中,它被理解为-128。
16位有符号整数
在16位有符号整数中,我们有足够的位来表示这两个数,因为16位有符号整数的范围是-32768到32767。
- 128:128的16位二进制表示是0000 0000 1000 0000。这里,最高位是0,表示它是正数。
- -128:-128的16位二进制表示是1111 1111 1000 0000。在这种情况下,最高位是1(表示它是负数),其余位是128的二进制表示的补码。
所以,-128的二进制码1000 0000是二进制补码表示法的一个特例。
同样的在16位有符号整数中,-32768是16位有符号整数中能表示的最小数,它的二进制补码表示是1000 0000 0000 0000,也是一个特例。