1.题目

输入一个长度为 $n$ 的整数序列。

接下来输入 $m$ 个操作，每个操作包含三个整数 $l,r,c$，表示将序列中 $[l,r]$ 之间的每个数加上 $c$。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 $n$ 和 $m$。

第二行包含 $n$ 个整数，表示整数序列。

接下来 $m$ 行，每行包含三个整数 $l，r，c$，表示一个操作。

输出格式
共一行，包含 $n$个整数，表示最终序列。

数据范围
$1\le n,m\le 100000,$
$1\le l\le r\le n,$
$-1000\le c\le 1000,$
$-1000\le 整数序列中元素的值\le 1000$

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

2.基本思想

前缀和的逆运算

类似于数学中的求导和积分，差分可以看成前缀和的逆运算。

差分数组：

首先给定一个原数组a：a[1], a[2], a[3],,,,,, a[n];

然后我们构造一个数组b ： b[1] ,b[2] , b[3],,,,,, b[i];

使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]

也就是说，a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。换句话说，每一个a[i]都是b数组中从头开始的一段区间和。

考虑如何构造差分b数组？

最为直接的方法

如下：

a[0 ]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] =a [3] - a[2];

........

b[n] = a[n] - a[n-1];

图示:

我们只要有b数组，通过前缀和运算，就可以在O(n) 的时间内得到a数组 。

话说有这么一个问题：

给定区间[l ,r ]，让我们把a数组中的[ l, r]区间中的每一个数都加上c,即 a[l] + c , a[l+1] + c , a[l+2] + c ,,,,,, a[r] + c;

暴力做法是for循环l到r区间，时间复杂度O(n)，如果我们需要对原数组执行m次这样的操作，时间复杂度就会变成O(n*m)。有没有更高效的做法吗? 考虑差分做法。

始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i]的修改，会影响到a数组中从a[i]及往后的每一个数。

首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c,,,,,, a[n] + c;

然后我们打个补丁，b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c;

为啥还要打个补丁？
我们画个图理解一下这个公式的由来:

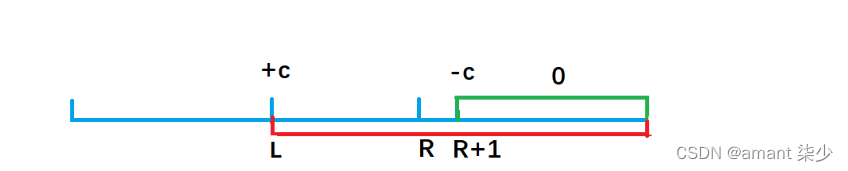
b[l] + c，效果使得a数组中a[l]及以后的数都加上了c(红色部分)，但我们只要求l到r区间加上c, 因此还需要执行 b[r+1] - c,让a数组中a[r+1]及往后的区间再减去c(绿色部分)，这样对于a[r] 以后区间的数相当于没有发生改变。

因此我们得出一维差分结论：给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c。时间复杂度为O(1), 大大提高了效率。
总结：

3.代码实现

import java.util.Scanner;

public class Main {
    static int N = 100010;
    static int[] a = new int[N], b = new int[N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(), m = sc.nextInt();
        for (int i = 1; i <= n; i++) a[i] = sc.nextInt();//读入数组
        for (int i = 1; i <= n; i++) insert(i, i, a[i]);//插入
        while (m-- > 0) {
            int l = sc.nextInt(), r = sc.nextInt(), c = sc.nextInt();
            insert(l, r, c);
        }
        for (int i = 1; i <= n; i++) {
            a[i] = b[i] + a[i - 1];//前缀和运算
            System.out.print(a[i] + " ");
        }//输出
    }

    private static void insert(int l, int r, int c) {
        b[l] += c;
        b[r + 1] -= c;
    }
}