难度参考
难度:中等
分类:栈与队列
难度与分类由我所参与的培训课程提供,但需要注意的是,难度与分类仅供参考。且所在课程未提供测试平台,故实现代码主要为自行测试的那种,以下内容均为个人笔记,旨在督促自己认真学习。
题目
根据逆波兰表示法,求表达式的值。
有效的运算符包括+,·,*,/。每个运算对像可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数
为0的情况。
示例1:
输入:["2","1","+","3","*门
输出:9
解释:该算式转化为常见的中缀算术表达式为:(2+1)*3)=9
示例2:
输入:["4","13","5","/","+"门
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4+(13/5)=6
思路
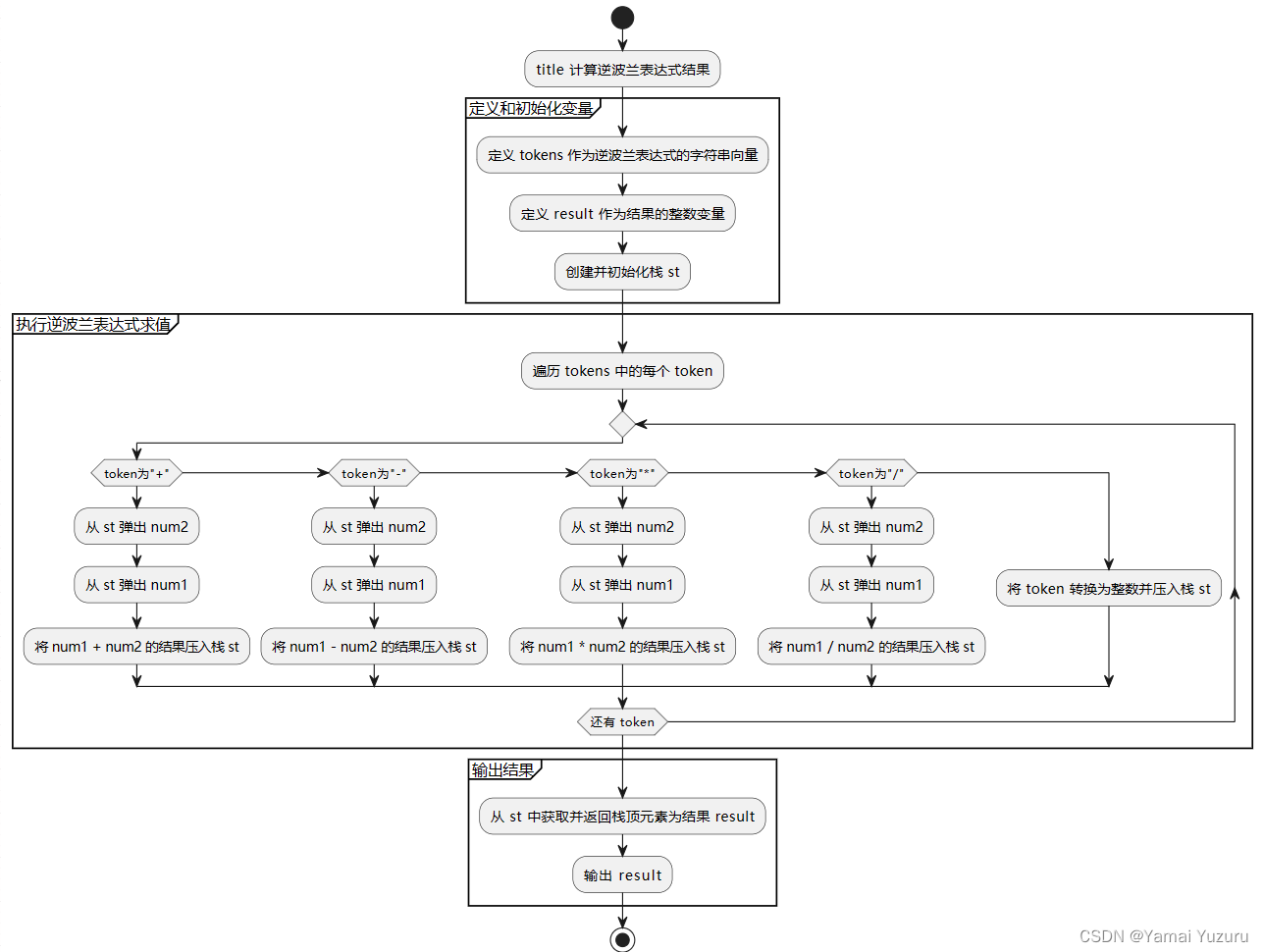
逆波兰表达式求解的一般思路是使用栈来存储操作数,然后遍历逆波兰表达式的每个元素,根据遇到的操作符进行相应的计算,并将结果重新入栈。遍历逆波兰表达式,并根据运算符进行相应的计算操作。
具体步骤如下:
- 定义一个栈,用于存储中间结果。
- 遍历逆波兰表达式,对于每个元素:
- 如果是数字,则将其转换为整数并压入栈中。
- 如果是运算符,则从栈中取出两个数字进行相应的运算。将运算结果压入栈中。
- 遍历结束后,栈中存储的元素即为表达式的最终结果。
示例
逆波兰表达式是一种不需要括号的数学表达式表示法,操作符位于操作数之后。
主要思路是使用一个栈来存储操作数,并依次遍历输入的表达式。当遇到操作符时,从栈中弹出对应数量的操作数,并根据操作符进行相应的运算,将运算结果压入栈中。当遍历完整个表达式后,栈中只会剩下一个元素,即表达式的最终结果。
举个例子来说明,假设我们要求解的逆波兰表达式是:2 1 + 3 *。我们依次遍历表达式中的每个字符:
- 第一个字符 “2” 是一个操作数,我们直接将其压入栈中;
"2", "1", "+", "3", "*" //字符 ^ st={2} //数字 - 第二个字符 “1” 是另一个操作数,同样将其压入栈中;
"2", "1", "+", "3", "*" //字符 ^ st={2, 1} //数字 - 第三个字符 “+” 是一个加法操作符,此时栈中的顶部两个元素分别是 1 和 2,我们将它们弹出并做加法运算得到 3,将结果 3 压入栈中;
"2", "1", "+", "3", "*" //字符 ^ st={3} //数字 - 第四个字符 “3” 是一个操作数,将其压入栈中;
"2", "1", "+", "3", "*" //字符 ^ st={3, 3} //数字 - 最后一个字符 “*” 是一个乘法操作符,此时栈中的顶部两个元素分别是 3 和 3,弹出并做乘法运算得到 9,将结果 9 压入栈中。
"2", "1", "+", "3", "*" //字符 ^ st={9} //数字
最终栈中只剩下一个元素 9,即为表达式的结果。
梳理
根据逆波兰表达式的性质,每当遇到一个操作符时,它前面的两个操作数已经被处理过并保存在栈中。所以,我们只需要从栈中弹出这两个操作数,根据操作符进行相应的运算,并将结果再次压入栈中。
- 没有括号:逆波兰表达式的特点是不需要括号来标识优先级,因为操作数和操作符的顺序已经明确,不存在歧义。
- 简化运算符的处理:由于操作符总是位于操作数之后,栈可以很方便地保存操作数。每当遇到一个操作符,只需要从栈中弹出所需的操作数进行运算,而不需要关心操作数之间的顺序或优先级。
- 遍历一次求解:由于逆波兰表达式的特点,我们只需要遍历一次表达式即可求解,无需进行多次迭代或递归。
总体来说,通过利用栈的先入后出(LIFO)的特性,将逆波兰表达式转化为了一种线性的、遍历一次即可求解的算法,从而实现了逆波兰表达式的求值。
代码
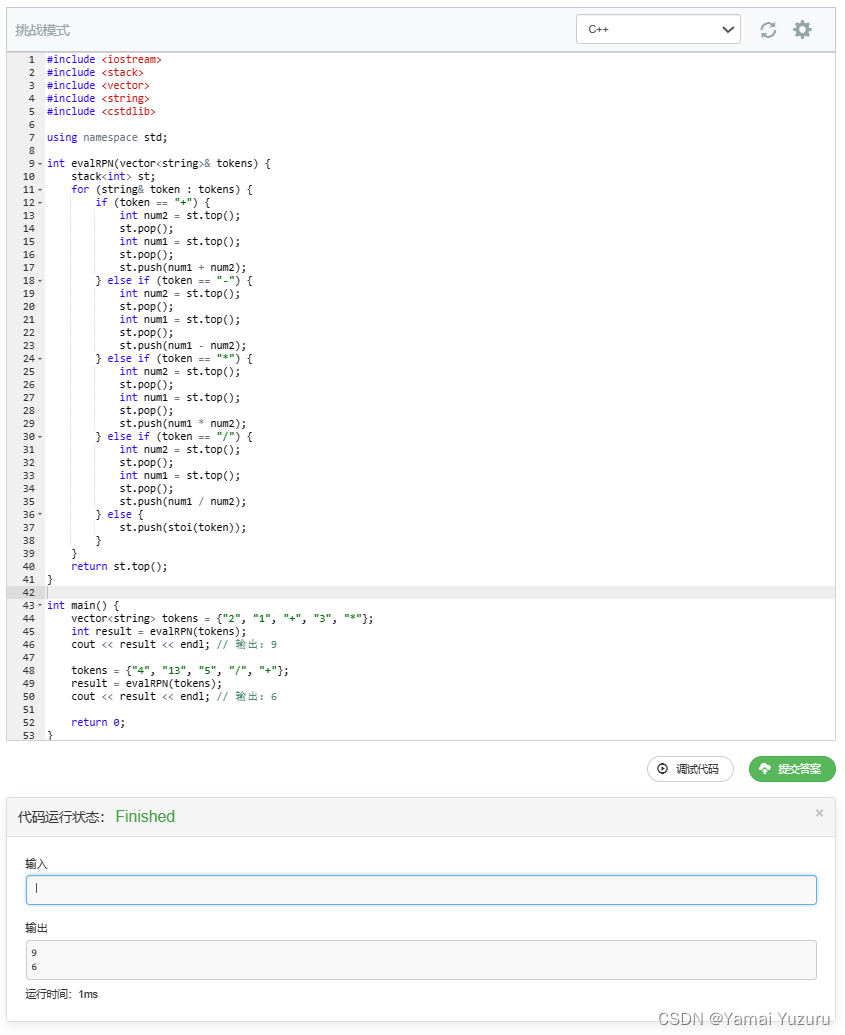
#include <iostream> // 包含输入输出流库,用于标准输入输出
#include <stack> // 包含栈库,用于存储操作数
#include <vector> // 包含向量库,用于存储输入的逆波兰表达式
#include <string> // 包含字符串库,用于操作字符串
#include <cstdlib> // 包含标准库,用于字符串转整数的函数
using namespace std; // 使用标准命名空间
int evalRPN(vector<string>& tokens) { // 定义了一个函数,用于计算逆波兰表达式的值,参数为存储表达式的向量
stack<int> st; // 创建一个整型栈对象,用于存储操作数
for (string& token : tokens) { // 遍历逆波兰表达式的每个元素
if (token == "+") { // 如果当前元素为加号
int num2 = st.top(); // 取出栈顶元素作为第二个操作数
st.pop(); // 弹出栈顶元素
int num1 = st.top(); // 取出新的栈顶元素作为第一个操作数
st.pop(); // 弹出栈顶元素
st.push(num1 + num2); // 将计算结果入栈
} else if (token == "-") { // 如果当前元素为减号,逻辑同上
int num2 = st.top();
st.pop();
int num1 = st.top();
st.pop();
st.push(num1 - num2);
} else if (token == "*") { // 如果当前元素为乘号,逻辑同上
int num2 = st.top();
st.pop();
int num1 = st.top();
st.pop();
st.push(num1 * num2);
} else if (token == "/") { // 如果当前元素为除号,逻辑同上
int num2 = st.top();
st.pop();
int num1 = st.top();
st.pop();
st.push(num1 / num2);
} else { // 如果当前元素为数字
st.push(stoi(token)); // 将字符串转换为整数后入栈
}
}
return st.top(); // 返回栈中最终的结果
}
int main() { // 主函数
vector<string> tokens = {"2", "1", "+", "3", "*"}; // 创建一个存储逆波兰表达式的向量,其中元素为字符串
int result = evalRPN(tokens); // 调用 evalRPN 函数计算表达式的值
cout << result << endl; // 输出计算结果
tokens = {"4", "13", "5", "/", "+"}; // 更新逆波兰表达式
result = evalRPN(tokens); // 调用 evalRPN 函数计算表达式的值
cout << result << endl; // 输出计算结果
return 0; // 返回 0,表示正常结束程序
}打卡