集合的基本概念

集合间的关系

特殊集合

集合的运算

以上都是高一学过的内容。

有穷集的计数（容斥定理）

序偶与集合的笛卡尔积

 

 

 

 

 

二元关系及其表示法

 

 

 

 

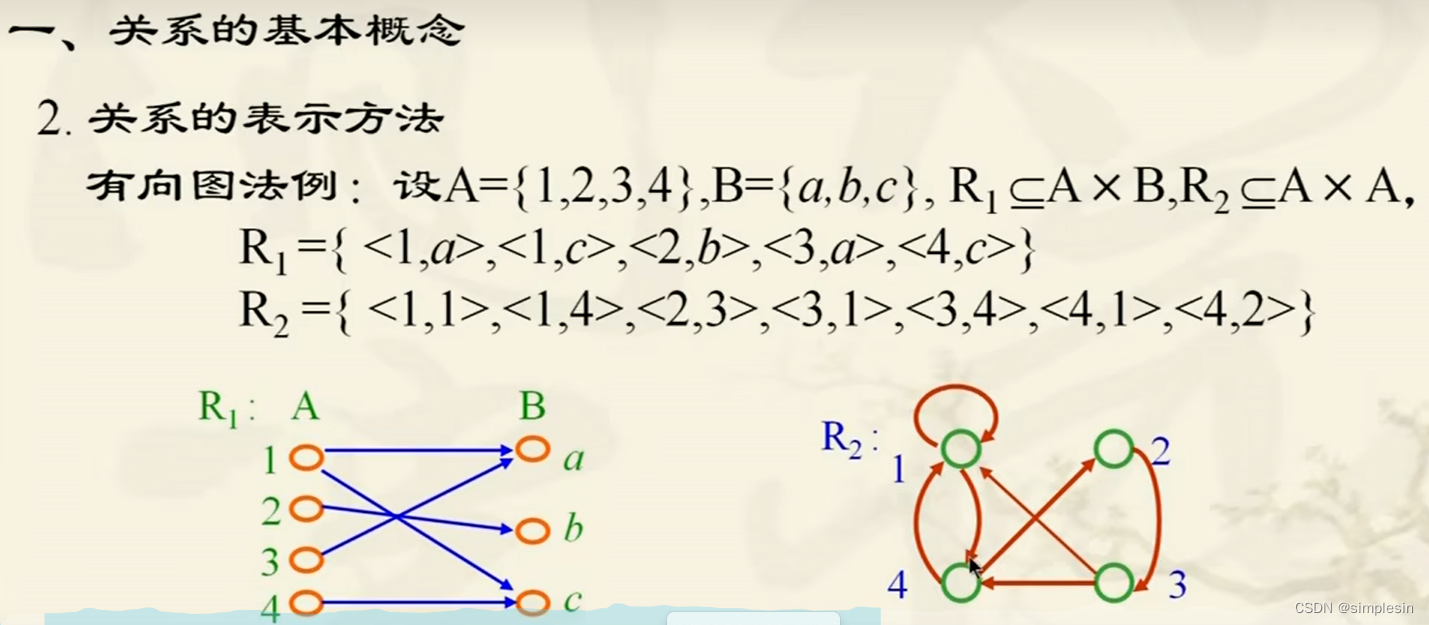
二元关系的性质

 

 

 

 

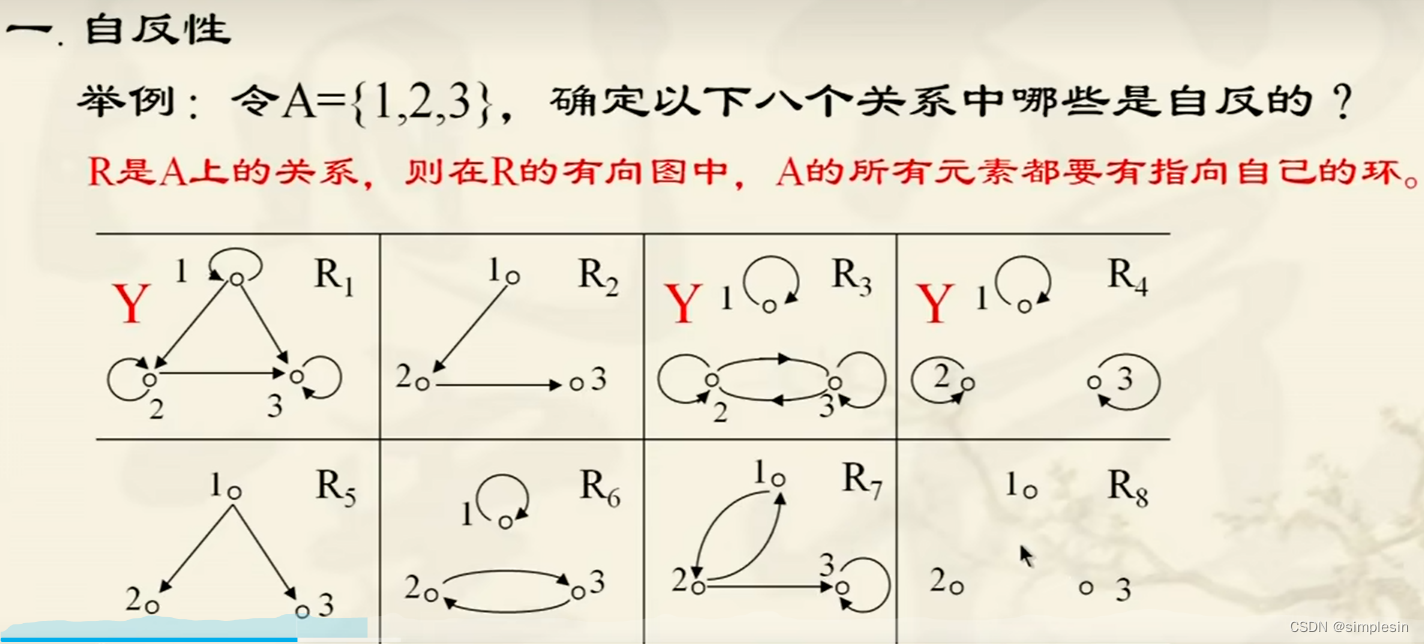
前件<x,y>,<y,z>后件<x,z>通过前件能推出后件，只有前真后假这一种情况整个推不出，则不具有传递性，其他情况均具有传递性 

 对于R3，有<x,x><x,y>也就是有<x，y><y，z>，也就是前件，也有后件<x，y>，就是x->y这条线既是条件，也是结论

对于R6，有<x,y><y,x>,前件是对的，但是没有后件，也就是没有<x,x>

 对于R2来说，有<x,y>也就是<1，2>，也有<y,z><2，3>，但是没有<1，3>，因此前件，也就是条件是对的，但是结论是错的。

我们知道，如果条件是错的，那不管结论是对的还是错的，那都是对的

如果条件是对的，那只有结论是对的，才是对的

如果条件是对的，结论是错的，则是错的。

关系的复合运算

 

 

 

关系的求逆运算

 

 

关系的闭包运算

不是很懂

集合的划分与覆盖

 

等价关系与等价类

相容关系与相容类

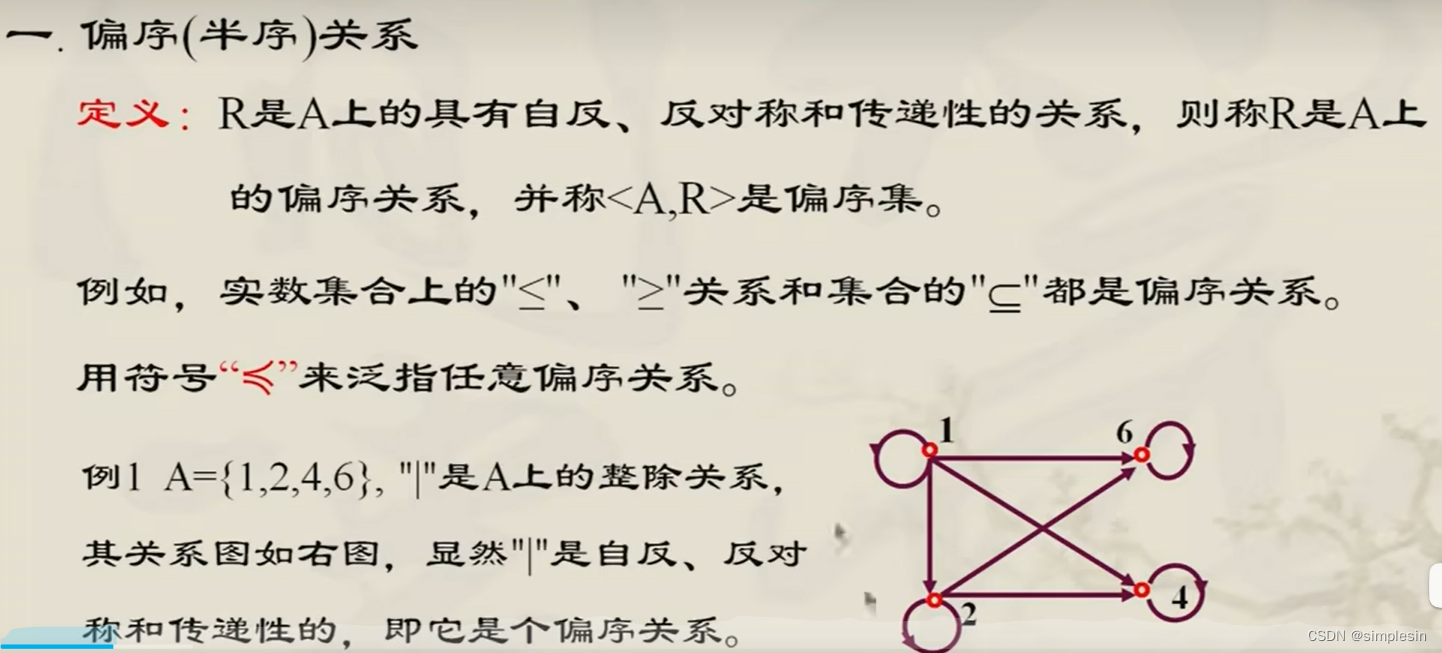
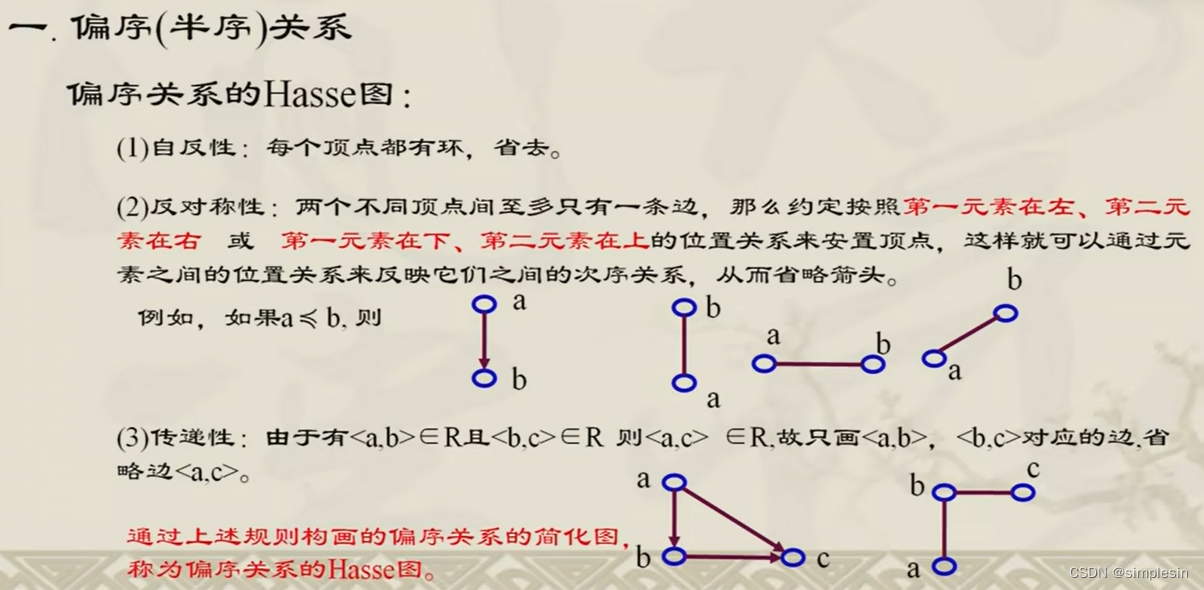
偏序关系