目录
- 参考文献
- 三维实体建模内核CSG/BREP
- Parasolid简介
- Parasolid接口函数
- Parasolid类的结构
- Parasolid数据分类:几何(Geometry)和拓扑(Topology)
- 拓扑(Topology)
- 什么是“拓扑”呢?
- Principle Geometry- Topology - Construction Geometry
- 案例:拓扑等价
参考文献
- https://mp.weixin.qq.com/s/1sVOUeCiKxWPESDOfETaeg作者:人月 [全球工业软件产业发展资讯](javascript:void(0)😉
- https://en.wikipedia.org/wiki/Solid_modeling
- https://en.wikipedia.org/wiki/ACIS
- https://en.wikipedia.org/wiki/Boundary_representation
- Parasolid Functional Description
三维实体建模内核CSG/BREP
大体上可以分为三种:线框模型、表面模型和实体模型。
实体建模指的是一组用于三维形状(实体)的数学和计算机建模的概念。实体建模与一般的几何建模和计算机图形学的相关领域(例如 3D 建模)的主要区别在于它强调物理保真度
实体模型基本上可以分为构造表示CSG(Constructive Solid Geometry)和边界表示BREP(Boundary Representation)两大类

图 . CSG表示法构造表示CSG(Constructive Solid Geometry)
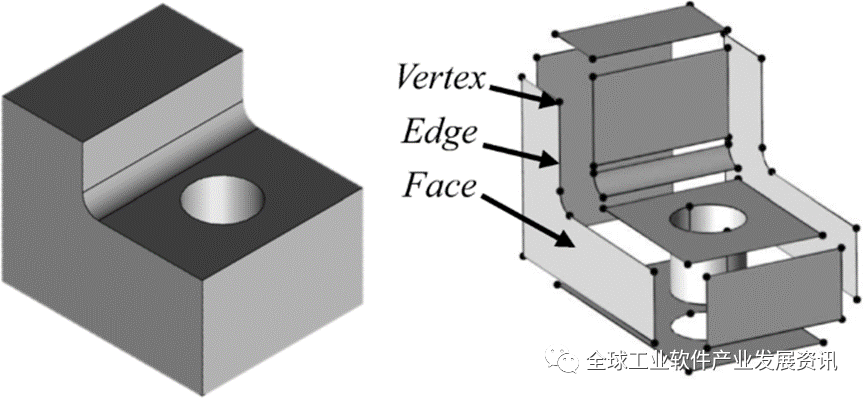
图 . B-rep表示法边界表示BREP(Boundary Representation)
目前市场上的主流建模内核主要有
西门子公司开发的Parasolid
达索公司的ACIS
开源的OpenCascade.
ACIS (Advanced CSG and Implicit Surfaces)
- 开发公司: 最初由Spatial Technology开发,后被Dassault Systèmes收购。
- 功能:
- 提供从简单到复杂实体的造型。
- 实体的布尔运算。
- 曲面裁剪和过渡编辑功能。
- 实体数据存储。
- 支持
SAT文件格式的导入导出。- 特点:
- 面向对象的数据结构。
- 使用C++编程语言。
- 灵活的线架造型、曲面造型、实体造型组合。
- 线架造型: 仅使用边和顶点定义物体。
- 曲面造型: 在线架造型基础上定义物体的可视面。
- 实体造型: 用物体的大小、形状、密度和属性(如重量、容积、重心)表示。
- 软件组件技术:
- 可自由组合使用ACIS的软件组件。
- 可以用自己开发的组件替换ACIS组件。
- 提供ACIS 3D Toolkit和多种专业软件包。
- 可定制性: 提供接口源程序,支持基于ACIS内核的系统开发,鼓励与STEP标准兼容的系统开发。
Open CASCADE (OCC)
- 类型: 开源几何造型引擎。
- 应用: 成为多款CAD/CAE/CAM软件的开发基础,如FreeCAD、HeeksCAD、AnyCAD。
- 特点:
- 基于BREP结构。
- 提供2D/3D实体造型和曲面造型。
- 逐渐增加的国内研究和使用情况。
- 组成:
- 建模核心组件。
- 可视化组件(基于
OpenGL,功能简单,显示效果一般)。- 数据管理(OCAF)(使用树状结构,复杂且效率较低,自定义扩展不便)。
Parasolid简介
什么是Parasolid呢?Parasolid是世界上领先的、经过生产证明的三维几何建模组件软件。
Parasolid是一种几何建模内核,由Siemens PLM Software开发,广泛应用于工程设计软件中。Parasolid的内核提供了一个富有表现力的API(应用程序编程接口),允许软件开发者在他们的应用程序中实现复杂的几何建模功能。
利用该软件提供的核心功能,基于Parasolid产品的用户能够快速、稳定地对行业最复杂的产品建模。由于基于高精度的边界表示技术(B-rep),
Parasolid支持在一个集成框架中进行实体建模、广义单元建模以及自由曲面建模。
Parasolid接口函数
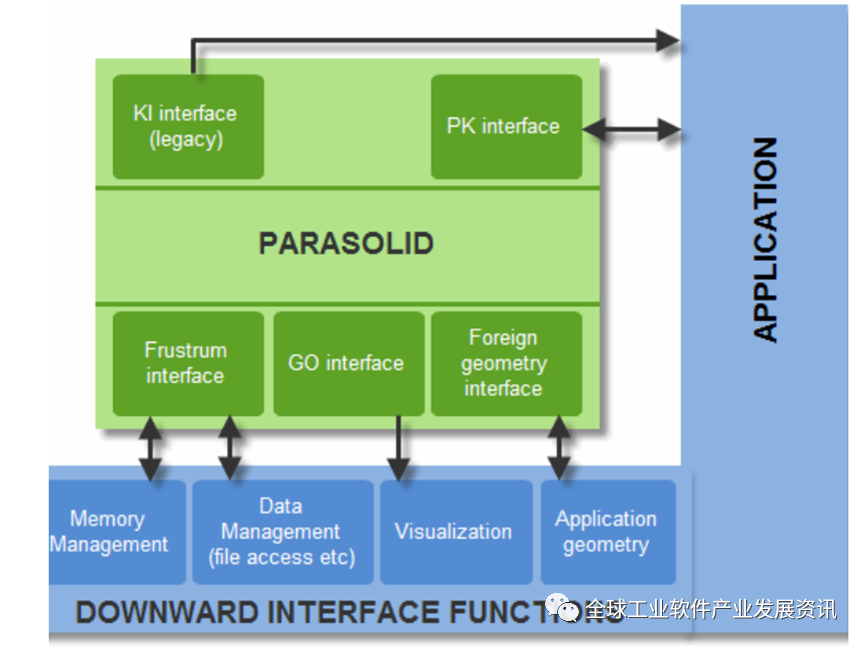
Parasolid中几个特定接口的简要解释:
-
Kl interface (legacy): Kl接口是Parasolid的
旧版API接口,通常保留用于向后兼容。"Legacy"意味着该接口可能已经不再是推荐使用的接口,但仍然被维护以支持旧软件或过时的功能。 -
PK interface: PK接口是Parasolid的主要
C语言API接口,提供了对Parasolid功能的全面访问。PK是"Parasolid Kernel"的缩写,该接口使得开发者能够利用内核的全部能力,如创建和编辑复杂的几何形状、执行布尔运算等。 -
Frustrum interface: Frustrum通常指的是图形学中的
视锥体,它是视觉观察空间的一部分。在Parasolid中,Frustrum interface可能指的是与几何视图或渲染有关的接口,用于处理和优化在特定视角下显示的几何数据。frustum
英/ˈfrʌstəm/美/ˈfrʌstəm
n.[数] 截头锥体;平截头体
-
GO interface: GO接口(
Geometric Operationsinterface)可能是指用于执行几何操作的接口,比如计算形状的交点、合并或切割形状等。这种接口通常包含一组函数,允许开发者在几何体上实施各种操作。 -
Foreign geometry interface: 在Parasolid中,Foreign geometry interface可能是指与
外部几何数据交互的接口。它允许Parasolid处理非Parasolid原生格式的几何数据,例如导入或导出到其他几何建模内核或CAD系统支持的格式。
Parasolid类的结构
根据Parasolid定义,可以在内核和用户的应用程序之间传递的数据项统统称为对象(Object)。每个对象都属于一个定义通用类型对象的类。Parasolid 中的类符合层次树的结构,如下图所示,最顶层的类是CLASS, 它是所有其它类型的父类。
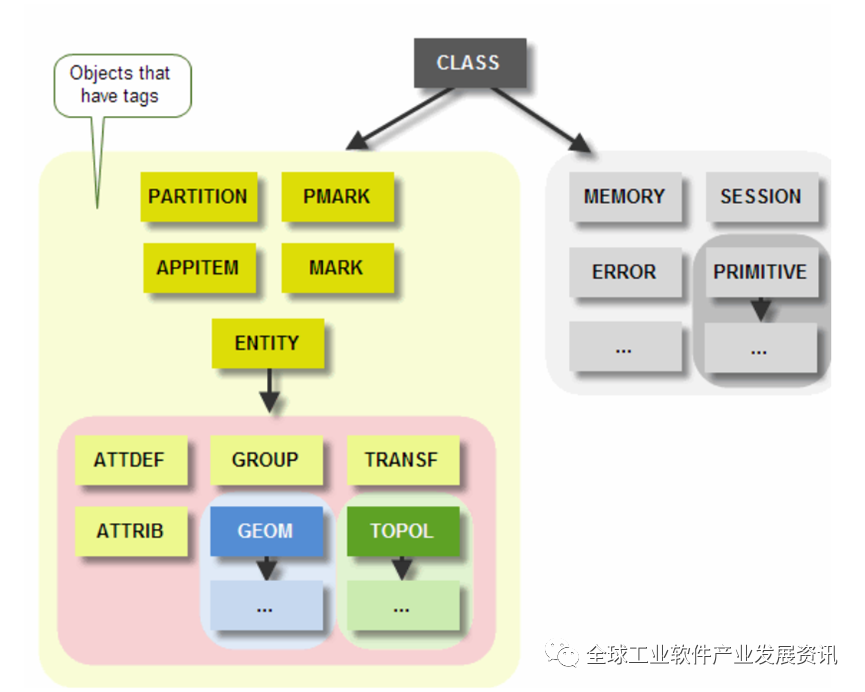
Parasolid模型中,标签(tags)是用于唯一标识实体的内部引用。标签允许应用程序和内核有效地引用和操作特定的几何和拓扑元素。例如,您可以使用标签来引用特定的几何实体,如点、线、面等,以便在算法中操作它们或在用户界面中显示信息。标签是Parasolid内核中实体管理的一部分,对于确保数据的一致性和完整性至关重要。
-
PARTITION: 在Parasolid中,Partition 指的是将复杂的几何模型
分割成更小的、可管理的部分,或者指代模型中的一个逻辑分区。partition
英/pɑːˈtɪʃ(ə)n/
美/pɑːrˈtɪʃ(ə)nn.隔墙,隔板;(国家的)分裂,分治;(化学)分离层;(计算机)存储分区;(数学)分割
v.分割,分裂(国家);(用隔板、隔扇等)隔开,分隔
-
PMARK: PMARK可能代表
标记点,用于在模型中指定位置,或者用于在执行某些操作(如修剪或分割)时标记几何特征。 -
APPITEM: APPITEM 是应用程序项目的简称,用于表示用户定义的数据或自定义数据项,这些数据可以附加到模型的不同部分。
-
MARK: 在Parasolid中,MARK通常用于
临时标记实体以便在操作过程中追踪它们,例如,在选择过程中标记多个实体以便对它们进行统一操作。 -
ENTITY: ENTITY是Parasolid中的基本构建块,指的是构成模型的
基本元素,如点、线、面、体等。 -
ATTDEF: ATTDEF 是
属性定义的缩写,用于定义可以附加到实体上的属性的结构或类型。 -
GROUP: GROUP可能指的是实体的
集合,允许将相关的实体组合在一起进行管理和操作。 -
TRANSF: TRANSF 指的是
变换,代表几何变换操作,如平移、旋转、缩放等。 -
ATTRIB: ATTRIB 是属性的缩写,用于表示附加到实体上的数据,如材料
属性、颜色、标签等。 -
GEOM: GEOM是
几何的简写,指的是模型中的几何元素,这可能包括点、线、曲线、面等。 -
TOPOL: TOPOL是
拓扑的简写,指的是模型的拓扑结构,如实体的边界表示(B-rep)等。
几何体的变换通常是通过变换矩阵来实现的,这在计算机图形学和几何建模中是一个标准的做法。变换矩阵是一个可以表示平移、旋转、缩放和倾斜等操作的数学工具。在三维空间中,这些变换通常通过4x4矩阵来表示。
下面是主要的几何变换和它们的矩阵表示:
平移(Translation): 平移操作通过添加一个常数向量到原始坐标来移动对象。平移矩阵如下:
[ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} 100001000010txtytz1 旋转(Rotation): 旋转操作围绕一个轴(x、y或z轴)旋转对象。例如,围绕z轴的旋转矩阵如下:
[ cos ( θ ) − sin ( θ ) 0 0 sin ( θ ) cos ( θ ) 0 0 0 0 1 0 0 0 0 1 ] \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 & 0 \\ \sin(\theta) & \cos(\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} cos(θ)sin(θ)00−sin(θ)cos(θ)0000100001
其中,θ 是旋转角度。
- 缩放(Scaling): 缩放操作通过乘以一个常数因子来改变对象的大小。缩放矩阵如下:
[ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} sx0000sy0000sz00001
- 倾斜或剪切(Shearing): 倾斜变换会沿着一个轴向另一个轴方向拉伸对象。剪切矩阵取决于剪切的类型和方向。
Parasolid数据分类:几何(Geometry)和拓扑(Topology)
在Parasolid里,按照使用目的一般把数据分为两类:几何(Geometry)和拓扑(Topology)。其中,
“几何”描述的是具体位置和形状,
“拓扑”描述的是邻接关系。
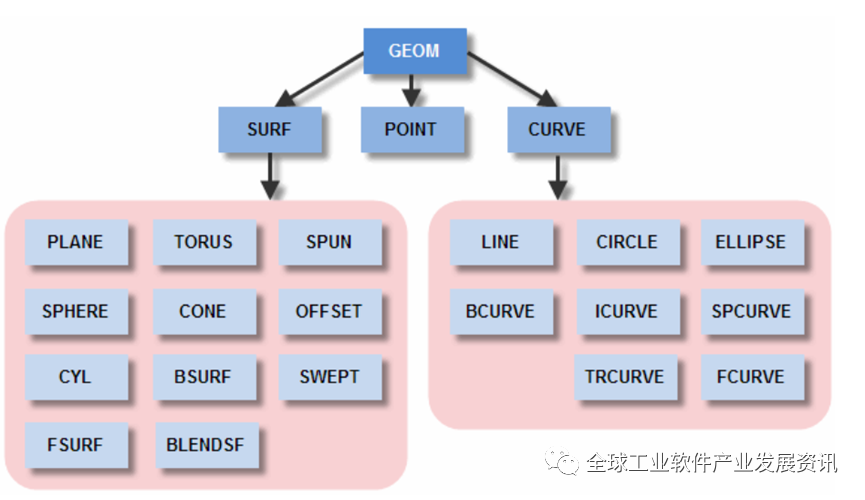
表面的不同类型:
-
PLANE: 平面。在三维空间中,平面是由两个非平行的向量定义的无限延伸的二维表面。
-
TORUS: 圆环体。一种形状类似于甜甜圈的三维几何体,由一个圆绕着另一个不在同一平面上的圆旋转生成。
torus
英/ˈtɔːrəs/
美/ˈtɔːrəs/
n. [植] 花托;圆环面;[解剖] 隆凸 -
SPUN: 旋转体。通过围绕一个轴旋转一个二维轮廓(如圆形、椭圆或其它形状)来生成的三维几何体。
spun
英/spʌn/
美/spʌn/v.(使)旋转;(使)急转身;纺线;结网;驾车飞驰(spin 的过去式及过去分词)
adj.纺制的
-
SPHERE: 球体。所有点与中心点等距离的三维几何体。
-
CONE: 圆锥体。一个有圆形底面的三维几何体,且底面中心到顶点的连线与底面垂直。
圆锥体;圆锥形物;锥形路标;(松树或冷杉的)球果;(盛冰淇淋的)锥形蛋卷筒,蛋筒冰激凌;视锥细胞;圆锥形山脉(或山峰)(尤指)火山锥;锥体,锥面;(在既定温度下融化的,用以测量窑温的)测温锥,示温锥;芋螺(=cone shell);
(尤指啤酒花藤的)球花;<英>用锥形交通路标分隔(或标明)道路(cone sth. off);使成锥形;【名】 (Cone)(英)科恩,(罗)科内,(塞)措内(人名);
-
OFFSET: 偏置。在几何建模中,偏置通常指创建一个与原始形状平行的曲面或体,两者之间有固定的距离。
-
CYL: 圆柱体。由两个相等的圆形底面和侧面组成的三维几何体,底面中心线是侧面的高线。
cylinder
-
BSURF: B样条曲面(B-Spline Surface)。利用B样条基函数定义的曲面,可以创建复杂的自由形状曲面。
-
SWEPT: 扫掠体/挤压体。由一个二维轮廓沿着一条直线或曲线路径"扫掠"或"挤压"出的三维几何体。
-
FSURF: 自由形曲面(Freeform Surface)。在CAD中,这通常指不由标准几何形状(如圆,平面等)定义的曲面,允许创建更复杂和有机的形状。
-
BLENDSF: 混合曲面(Blend Surface)。用于在两个或多个曲面之间创建平滑过渡的曲面,常用于圆角和过渡区域。
曲线的不同类型:
-
LINE: 直线。在三维空间中,直线可以无限延伸,但在计算机几何中,通常会有起点和终点来定义一条线段。
-
CIRCLE: 圆。所有点到一个固定中心点的距离相等的平面闭合曲线。
-
ELLIPSE: 椭圆。平面上一种闭合曲线,其中任一点到两个固定点(焦点)的距离之和是常数。
英/ɪˈlɪps/
美/ɪˈlɪps/
n.[数] 椭圆形,[数] 椭圆 -
BCURVE: B样条曲线(B-Spline Curve)。通过一组
控制点和B样条基函数定义的曲线,可以灵活地表示形状。 -
ICURVE: 插值曲线(Interpolating Curve)。一种通过
一组点并且曲线通过这些点的曲线。 -
SPCURVE: 特殊曲线(Special Curve)。这个术语不是标准的CAD术语,它可能特指某一款软件中的特定曲线类型,或者是一个统称,指的是任何特殊形式或属性的曲线。
-
TRCURVE: 转换曲线(Transformed Curve)。这可能指的是经过几何变换(如平移、旋转、缩放等)的曲线。
-
FCURVE: 自由形曲线(Freeform Curve)。通常是指不受简单几何形状约束的曲线,可以是任意形状的曲线,常用于描述复杂的或有机形状的边界。
拓扑(Topology)
什么是“拓扑”呢?
它是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的一个概念, 它只考虑物体间的位置关系而不考虑它们的形状和大小。
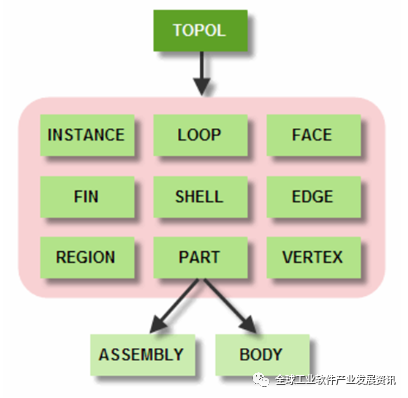
图 . Parasolid的拓扑类型
在CAD、CAM和CAE系统中。Parasolid的数据模型包括多种拓扑实体类型,每种类型都代表了三维空间中的不同几何和拓扑构件。以下是Parasolid拓扑类型的简要说明:
-
INSTANCE: 一个实例(Instance)代表了一个复杂的
几何体或者拓扑结构的副本。这允许在不同的位置、尺寸或方向重复相同的几何体而不需要重新定义几何体本身。
-
LOOP: 在面拓扑结构中,环(Loop)是定义一个面边界的边的集合。一个面可以有一个
外环(定义外边界)和多个内环(定义洞或内部边界)。 -
FACE: 面(Face)是一个二维的几何实体,表现为三维空间中的曲面。在Parasolid中,
一个面由一个或多个环定义,这些环标识了面的边界。 -
FIN: 鳍(Fin)是两个相邻面之间的
共享边。在Parasolid中,鳍是边(Edge)和面(Face)的连接,它表示了面之间的连接。英/fɪn/美/fɪn/
n.(鱼的)
鳍;鳍状物,(飞机或汽车的)尾翅,尾翼;(潜水者的)脚蹼;散热片v.(穿着脚蹼)在水下游泳
【名】 (Fin)(法)芬(人名)
-
SHELL: 壳(Shell)是构成
实体(Solid)的面的集合。一个实体可以由一个外壳(定义外部边界)和多个内壳(定义空腔或孔洞)组成。 -
EDGE: 边(Edge)是一个
一维的几何实体,它代表了两个顶点之间的直线或曲线段。在Parasolid的拓扑结构中,边是环的组成部分。 -
REGION: 区域(Region)是一组
相连的壳。它通常用来表示具有共同边界的一组面,例如,一个壳可能被分割成多个区域以便于处理。 -
PART: 零件(Part)是Parasolid中的一个基本单位,可以包含一个或多个实体(Solids)。它代表了一个完整的三维模型或模型的一个部分。
-
VERTEX: 顶点(Vertex)是一个
零维的几何实体,它代表了空间中的一个点。在拓扑结构中,顶点是边的端点。
Parasolid中的这些拓扑类型是构建和操作复杂三维模型的基础,它们之间的关系定义了模型的几何形状和拓扑连续性。通过这些类型,可以对模型进行各种操作,如布尔运算、修剪、偏移和复杂形状的创建等。
所以在Parasolid中,所有的拓扑类型按照边界表示法共构成了模型的骨架。
Principle Geometry- Topology - Construction Geometry
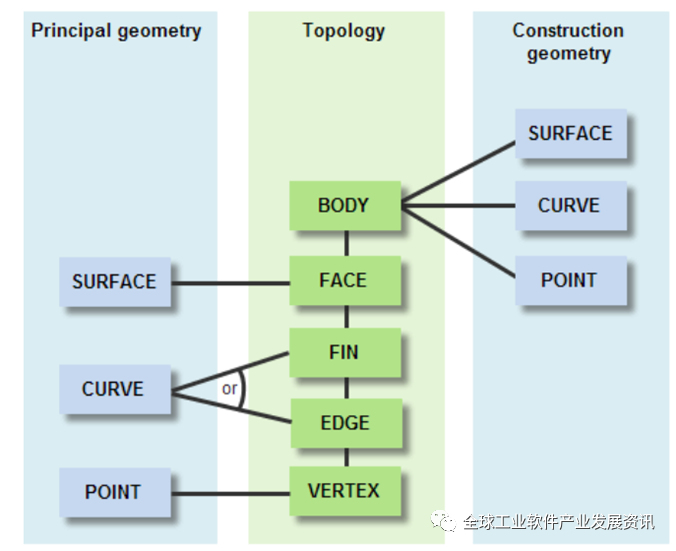
图 . Parasolid的拓扑类型和几何类型的联系
附着在某一特定拓扑上的几何类型(Surface, Curve, Point)构成了模型具体的形状和位置,Parasolid把这一类几何称为Principle Geometry。与之相对的,只附着在体(Body)上的几何,Parasolid称之为Construction Geometry。例如,用户需要用一个点来表示体的质心,那么就可以创建这个点然后附着在Body上。
案例:拓扑等价
为什么要有“拓扑”的概念?
“拓扑”(Topology)的概念源于数学,特别是几何学的一个分支,它研究空间的属性和结构,这些属性在连续变形下保持不变,如伸展、弯曲和扭曲,但不包括撕裂或粘合。在数学以外的领域,如计算机科学、网络理论、和物理学等,拓扑的概念也有其独特的应用和重要性。
拓扑的概念之所以重要,是因为它允许我们抽象地理解和描述物体或系统的连续性和关系,而不依赖于其精确的几何形状。这样可以使我们更容易地分析和解决复杂的问题。
数学和几何学中的拓扑
在数学中,拓扑关注的是对象如何连接在一起,以及它们如何形成一个连续的整体。例如,一个咖啡杯和一个甜甜圈(圆环)在拓扑学中是等价的,因为一个可以通过无穷的橡胶伸展变形成为另一个,咖啡杯的把手相当于甜甜圈的一个洞。
计算机科学中的拓扑
在计算机科学中,拓扑结构被用于描述网络中的布局。例如,在网络拓扑中,不同的布局,如星形拓扑、环形拓扑和总线拓扑等,对于理解网络的性能和通信模式至关重要。
工程和技术中的拓扑
在使用CAD(计算机辅助设计)软件进行产品设计时,拓扑概念帮助工程师理解和设计零件的连通性和相互作用。例如,一个复杂的机械装置(Body)可以被分解成多个零件(Parts)和子装配体(Sub-assemblies),它们之间的关系可以通过拓扑结构来描述。
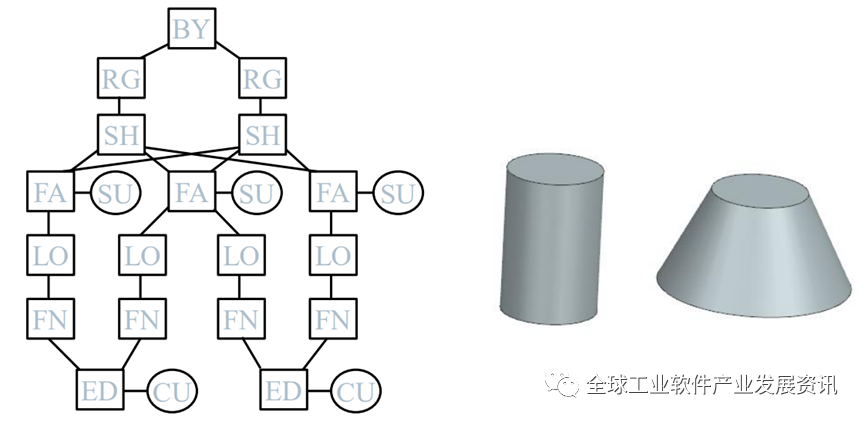
图 . Parasolid的拓扑结构示例
从上图的示例中我们可以去更直观的感受到拓扑其实只是模型的骨架。图中圆柱和圆台虽然形状不一样,但是他们有相同的拓扑结构,在拓扑学的框架下,圆柱(Cylinder)和圆锥台(Frustum,一种圆锥的一部分,典型的圆锥台是有两个平行的圆形底面,底面之间连接的侧面是斜的)通常被视为拓扑等价的,因为它们都可以被看作是具有两个圆形边界的三维物体。这意味着,如果我们允许连续的、不撕裂的变形,则可以将一个圆柱形变形为一个圆锥台,反之亦然。
在拓扑学中,两个对象如果可以通过拉伸、压缩等连续变形(称为同胚)而不是通过切割或黏合来相互转换,则它们被认为是拓扑等价的。圆柱和圆锥台之间的差异仅在于它们的几何形状和尺寸,而不影响它们的拓扑性质。具体来说:
- 圆柱具有两个平行且大小相同的圆形底面,以及一个连接这两个底面的侧面。
- 圆锥台具有两个平行但大小不同的圆形底面,以及一个斜面(侧面),在高度方向上连接这两个底面。
在拓扑学的视角中,这两种形状都可以被看作是由一个侧面和两个边界组成,因此在没有撕裂和黏合的情况下,它们是可以相互连续变形的。因此,从拓扑的角度来看,它们是相同的。这就是为什么在拓扑学中,圆柱和圆锥台被认为是拓扑上没有区别的。