前言

经过上一章节对于 union-find 算法的实现以及分析，这一章节主要是对于算法的一些分析以及理论性的总结说明，还包含三数之和的实现以及优化、二分查找的实现以及证明等。

需要说明一下，Sedgewick 教授讲解第一章的顺序不是按照书本的编排顺序，而是先讲了实例，再对算法分析进行总结，然后再到基础理论说明，即 1.5 到 1.4 再到 1.3（1.1 和 1.2 没有讲，主要是 Java 相关的内容，但实际上算法课是没有语言限制的，可能有 Java 基础的话看这本书会比较舒服，但是如果是听教授讲课我觉得影响不大）。

参考目录

• B站 普林斯顿大学《Algorithms》视频课
  （请自行搜索。主要以该视频课顺序来进行笔记整理，课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。）
• 微信读书《算法（第4版）》
  （本文主要内容来自《1.4 算法分析》）
• 官方网站
  （有书本配套的内容以及代码）

学习笔记

注1：下面引用内容如无注明出处，均是书中摘录。
注2：所有 demo 演示均为视频 PPT demo 截图。

1：科学方法

本章开篇首先说明的是应用于算法研究的科学方法以及其原则。

（截图自官方文档）

（用官网的英文原版是便于直观展示每一个强调的点）

再贴一下中译版：

2：观察举例：三数之和

简单说明一下三数之和，即输入一组整数，需要统计出所有和为 0 的三整数数组的数量。

首先，最容易想到的便是暴力算法。

edu.princeton.cs.algs4.ThreeSum#count

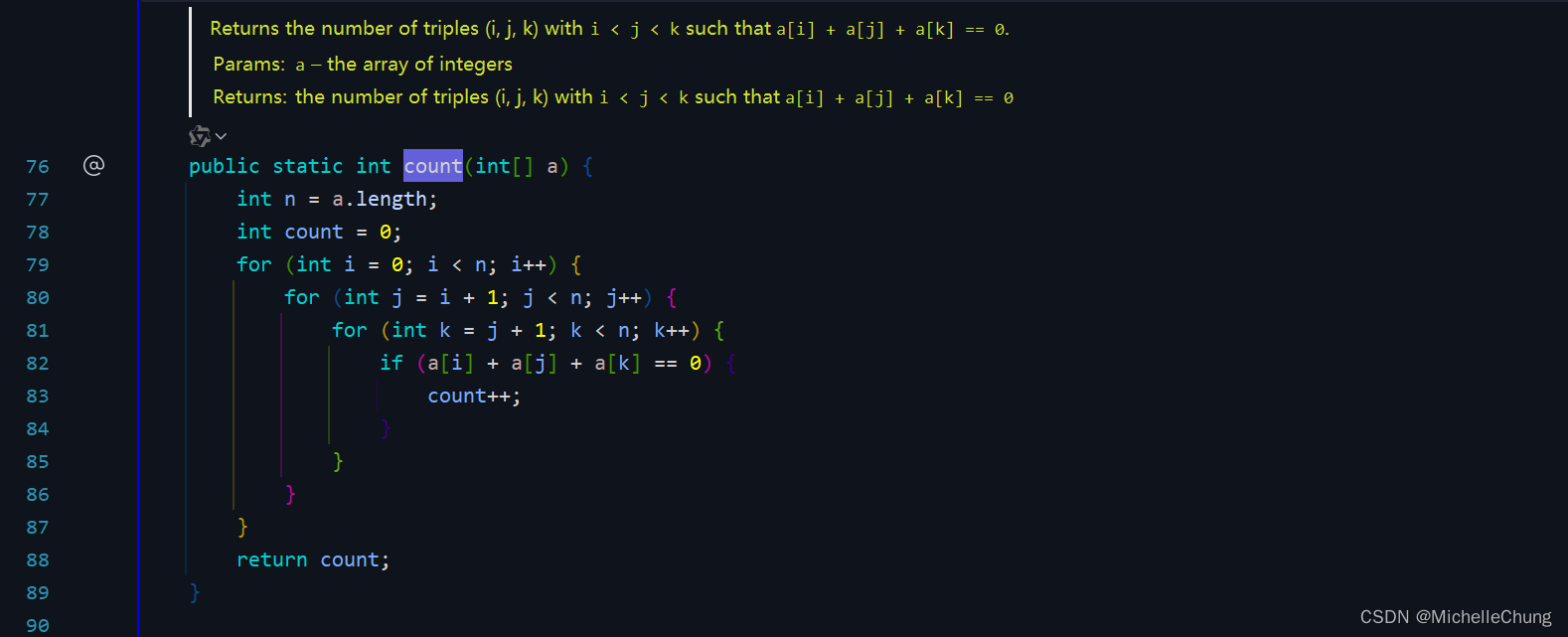
三重循环，由已有的运行时间记录推算得到的运行时间大致为：

T(N)=9.98×10^-11×N³

3：近似

一个程序运行的总时间主要和两点有关：
❏执行每条语句的耗时；
❏执行每条语句的频率。
前者取决于计算机、Java编译器和操作系统，后者取决于程序本身和输入。

我们常常使用约等于号（～）来忽略较小的项，从而大大简化我们所处理的数学公式。该符号使我们能够用近似的方式忽略公式中那些非常复杂但幂次较低，且对最终结果的贡献无关紧要的项。

4：增长数量级

表1.4.7 对增长数量级的常见假设的总结

在增长数量级这一节中，主要以二分查找来进行说明。

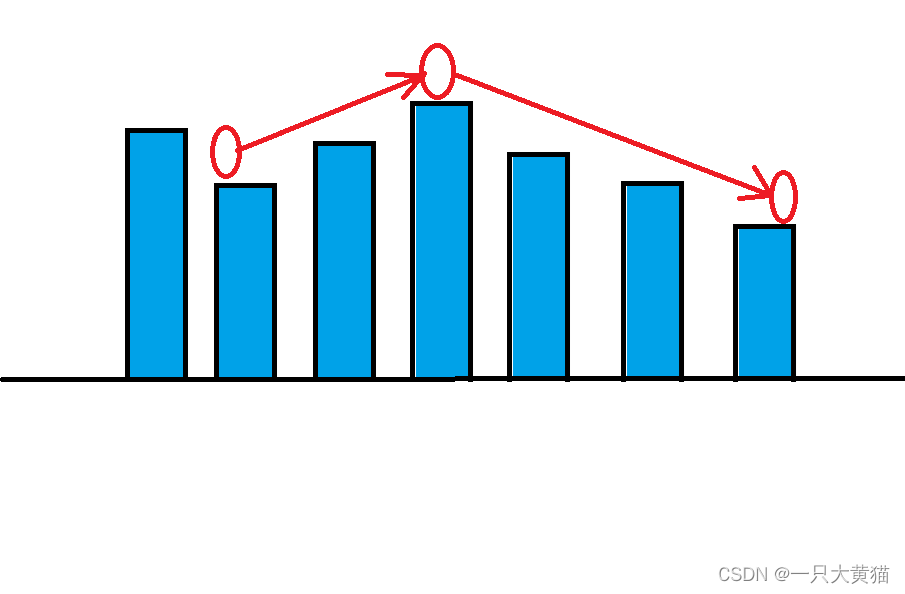
4.1：二分查找 demo

简单说明二分查找的demo：

给定一个排序好的数组以及一个key，查到key在数组中的下标。

实现方式：

二分查找：循环比较key和数组中间的元素

• 如果key小，往左；
• 如果key大，往右；
• 相等，返回。

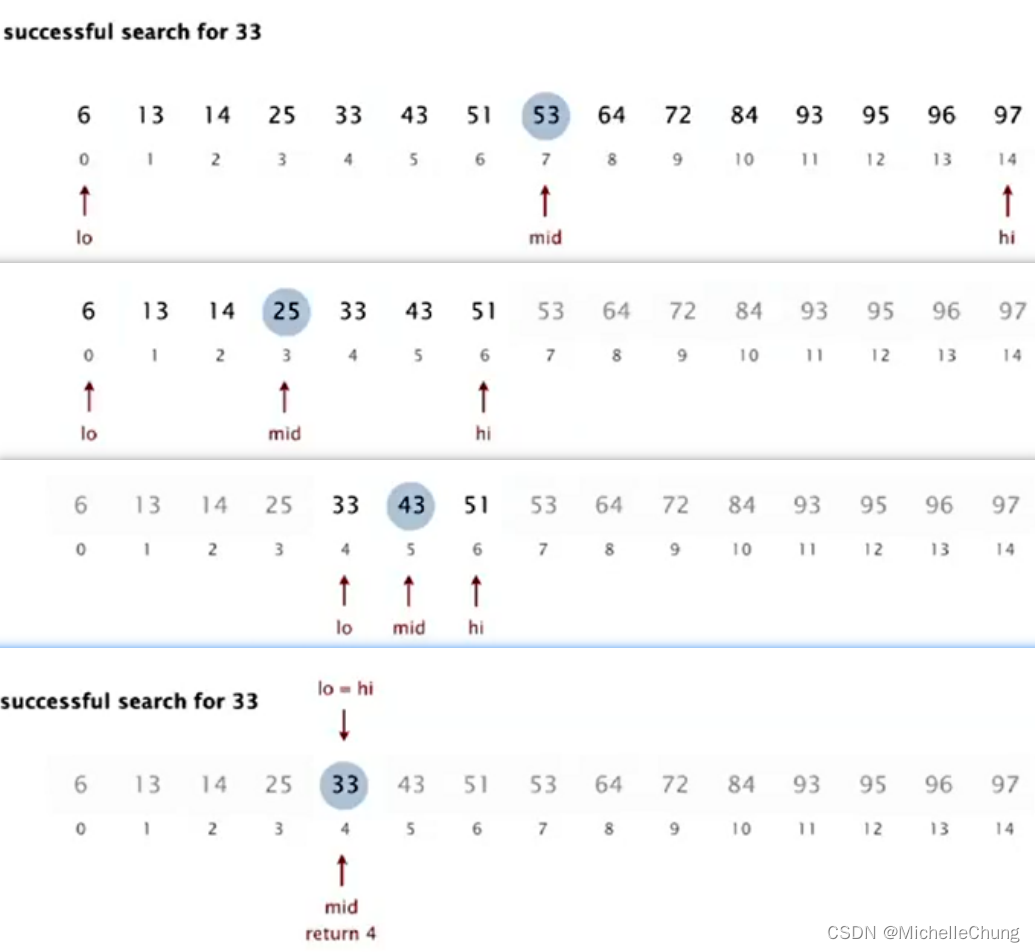
在一组排序好的数字中找到整数 33 的下标：

4.2：二分查找代码实现

edu.princeton.cs.algs4.BinarySearch#indexOf

4.3：二分查找比较次数的证明（比较次数最多为lgN+1）

先看下教授给出的证明方式：

但是吧，我数学真的一般般，所以我又去问了一下通义，所幸看懂了它给出的证明步骤：

（格式有点问题，我就直接贴原文了，有些描述进行了修改）

二分查找（Binary Search）在每次迭代中都会将搜索范围减半，直到找到目标值或者搜索范围缩小到不存在为止。假设我们有一个包含n个元素的有序数组（比如升序排列），初始搜索范围是整个数组，即从索引0到n-1。

证明步骤：

1. 初始化比较次数k=0，表示开始时还未进行任何比较。

2. 每次迭代，我们将当前搜索区间划分为两半，取中间元素与目标值进行比较。如果相等，则找到了目标值并停止搜索；如果不相等，根据比较结果舍弃一半区间（不包含目标值的那一半）。

3. 由于每次比较后至少会排除掉原来区间的一半，因此，在第k次迭代后剩余的区间长度为 n 的 部分。

   对于长度n的数组，k=0是，剩余部分为 1/(2⁰) = 1；
   以此类推，剩余部分为 1/(2¹) = 1/2；1/(2²) = 1/4；1/8；1/16……

4. 我们的目标是确定最大的比较次数，使得剩下的区间长度为1（即只剩一个元素或刚好找到目标值）。这意味着：
   $$n/2^k=1$$

5. 解这个方程得到：
   $$k=log2(n)$$

6. 因为实际情况下k必须是整数，并且计算机程序中通常使用向下取整来决定迭代次数，所以实际上最大迭代次数是。

7. 但是，当 log₂(n) 不是整数时，需要再进行一次迭代以确定最后一个元素是否为目标值，所以总共的最大比较次数应该是向下取整的基础上加1：
   $$最大比较次数=\lfloor {\log }_2(n)\rfloor +1$$

8. 这意味着对于任意大小为n的有序数组，最多需要执行第 7 点中计算得到的比较次数就能确定目标值是否存在。

5：三数之和的优化

对于 2 中三数之和的暴力算法，这里提出了一种利用二分查找进行优化的方法：

• 升序排列非重复的一组数字
• 对于每一对组合 a[i] 和 a[j]，利用二分查找寻找是否存在 -(a[i]+a[j])

5.1：三数之和优化代码实现

edu.princeton.cs.algs4.ThreeSumFast#count

6：上下界

这一部分属于理论性比较强的内容，主要是说明了这个概念对于算法研究的必要性。

同样贴一下通义关于上下界概念的说明，便于理解：

算法上下界是指在分析算法性能时，对算法执行时间或空间复杂度的一个范围的界定。这个范围可以帮助我们更好地了解算法在不同情况下的表现，并对算法进行更全面的评估。

1. 算法上界（Upper Bound）：

   • 定义：算法在最坏情况下的执行时间或空间复杂度的一个上限。
   • 作用：提供了算法性能的悲观估计。上界告诉我们，在最不利的情况下，算法的性能不会超过这个值。这对于确保算法在任何情况下都能在合理的时间内完成任务很有帮助。

2. 算法下界（Lower Bound）：

   • 定义：算法在最好情况下的执行时间或空间复杂度的一个下限。
   • 作用：提供了算法性能的乐观估计。下界告诉我们，在最理想的情况下，算法的性能不会低于这个值。这对于了解算法的优势和在最优情况下能够达到的极限非常重要。

3. 平均情况复杂度：

   • 平均情况复杂度考虑了算法在所有可能输入下的性能。它可以被视为上界和下界的平均值。

在分析算法性能时，我们通常关注最坏情况下的上界，因为这提供了对算法在任何情况下的性能都足够保守的估计。同时，下界可以帮助我们了解算法的潜在优势。

作用：

1. 性能保证： 算法上界提供了对算法在最坏情况下性能的保证，这对于实际应用中的稳定性和可靠性至关重要。

2. 算法选择： 在设计和选择算法时，我们可以根据算法的上下界来判断它是否满足问题的要求。较低的上界和较高的下界通常是理想选择的标志。

3. 问题难度： 下界可以用来表征特定问题的难度。如果一个问题的下界很高，说明在任何情况下找到更好的算法可能是困难的。

4. 理论研究： 上下界有助于理论计算机科学的研究，因为它们提供了对问题复杂性的深刻理解，而不仅仅是特定算法的表现。

总体来说，算法上下界的定义和分析有助于我们更全面地理解算法的性能，并在设计和选择算法时做出明智的决策。

（完）