机器学习-3降低损失(Reducing Loss)

学习内容来自：谷歌ai学习
https://developers.google.cn/machine-learning/crash-course/framing/check-your-understanding?hl=zh-cn
本文作为学习记录

1.降低损失：迭代方法

迭代学习
下图展示了机器学习算法用于训练模型的迭代试错过程：

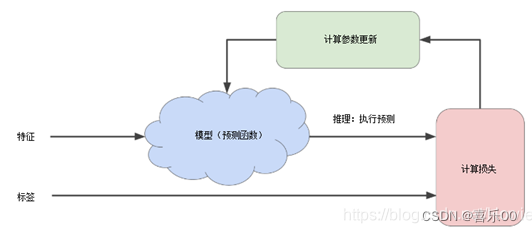
迭代策略在机器学习中很常见，主要是因为它们可以很好地扩展到大型数据集。
“模型”将一个或多个特征作为输入，并返回一项预测作为输出。为简单起见，假设一个模型接受一个特征 ( X1) 并返回一个预测 (y’)：
y’ = b + $w_1$ $x_1$**

最后，我们已经到达图中的“计算参数更新”部分。机器学习系统会在这里检查损失函数的值，并为b 和 w1生成新值。现在，我们先假设这个神秘的框会产生新值，然后机器学习系统会根据所有标签重新评估所有特征，为损失函数生成一个新值，而该值又产生新的参数值。学习过程会持续迭代，直到该算法发现损失可能最低的模型参数。通常，您可以反复迭代，直到整体损失不再发生变化或变化速度至少变化得非常缓慢。这时候，我们可以说该模型已收敛。

训练机器学习模型时，首先对权重和偏差进行初始猜测，然后以迭代方式调整这些猜测，直到学习出损失可能最低的权重和偏差。

2. 降低损失：梯度下降法 Gradient Descent

迭代方法图包含一个标题为“计算参数更新”的华而不实的绿色方框。我们现在要用更实质的方法代替这种精明的算法。

理解梯度下降就好比在山顶以最快速度下山：好比道士下山，如何在一座山顶上，找到最短的路径下山，并且确定最短路径的方向

假设我们有时间和计算资源来计算w1的所有可能值的损失。对于我们一直在研究的那类回归问题，产生的损失与w1的图表始终是凸形。换句话说，图表将始终是碗状图，如下所示： 图 2. 回归问题产生的损失与权重图呈凸形。

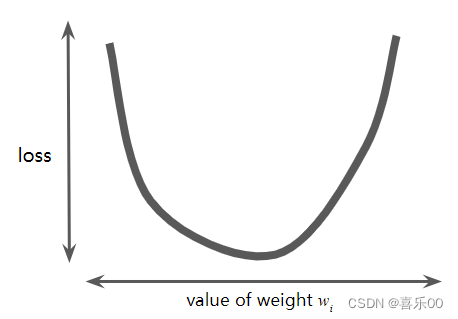
凸形问题只有一个最小值；即只有一个位置的斜率正好为 0。这个最小值就是损失函数收敛的位置。
通过计算整个数据集内每个w1可能的值的损失函数来寻找收敛点的效率非常低下。我们来研究一种更好的机制，这种机制在机器学习领域非常热门，称为梯度下降法。
通过计算整个数据集中 每个可能值的损失函数来找到收敛点这种方法效率太低。我们来研究一种更好的机制，这种机制在机器学习领域非常热门，称为梯度下降法。
梯度下降法的第一阶段是为w1选择一个起始值（起点）。起点并不重要；因此，许多算法直接将w1设置为 0 或选择随机值。在下图中，我们选择了一个略大于 0 的起点：
然后，梯度下降法算法会计算损失曲线在起点的梯度。在图 3 中，损失的梯度等于曲线的导数（斜率），可以告诉您哪个方向是“更暖”还是“冷”。当有多个权重时，梯度是偏导数相对于权重的矢量。

执行梯度下降法时，我们会泛化上述过程，以同时调整所有模型参数。例如，为了找到w1和b偏差的最优值，我们会同时计算w1和b的梯度。接下来，我们根据w1和b各自的梯度修改它们的值。然后重复上述步骤，直到达到最小损失。

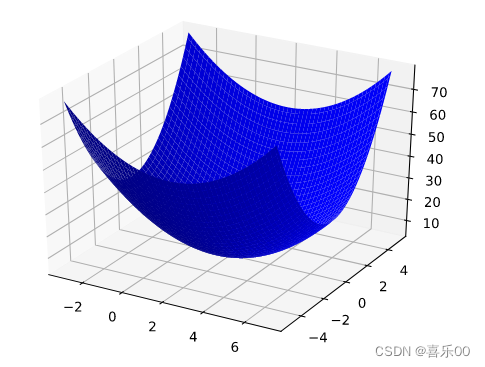
原理上就是凸形问题求最优解，因为只有一个最低点；即只存在一个斜率正好为 0 的位置。这个最小值就是损失函数收敛之处。

梯度下降法的目标：寻找梯度下降最快的那个方向
梯度是一个矢量，因此具有以下两个特征：方向、大小
梯度始终指向损失函数中增长最为迅猛的方向。梯度下降法算法会沿着负梯度的方向走一步，以便尽快降低损失

为了确定损失函数曲线上的下一个点，梯度下降法算法会将梯度大小的一部分与起点相加

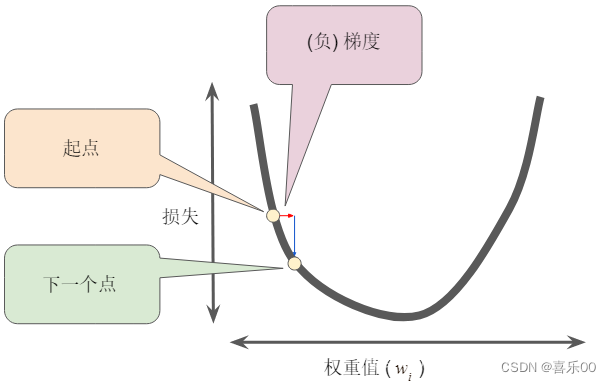
然后，梯度下降法会重复此过程，逐渐接近最低点。（找到了方向）

3.降低损失 (Reducing Loss)：学习速率

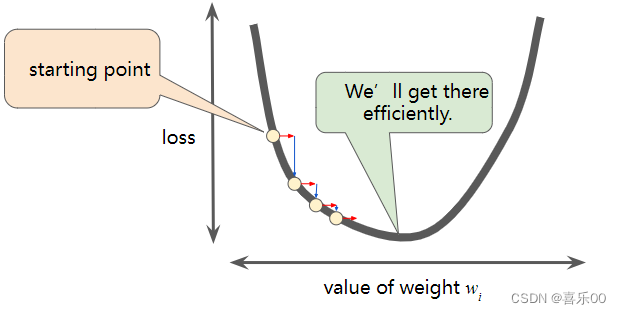
超参数是编程人员在机器学习算法中用于调整的旋钮。大多数机器学习程序员都会花费大量时间来调整学习速率。如果您选择的学习速率过小，则学习将会花费太长时间：
相反，如果您指定的学习速率过大，则下一个点将永远在井底随意弹跳，就像量子力学实验大错一样：
每个回归问题都存在一个金发姑娘学习速率。“金发姑娘”值与损失函数的平坦程度有关。如果您知道损失函数的梯度较小，则可以放心地尝试较大的学习速率，以抵消小的梯度，从而产生较大的步长。

3.1黑塞矩阵（Hessian Matrix）

黑塞矩阵又译作海森矩阵、海瑟矩阵、海塞矩阵等，是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。

4.降低损失：优化学习速率

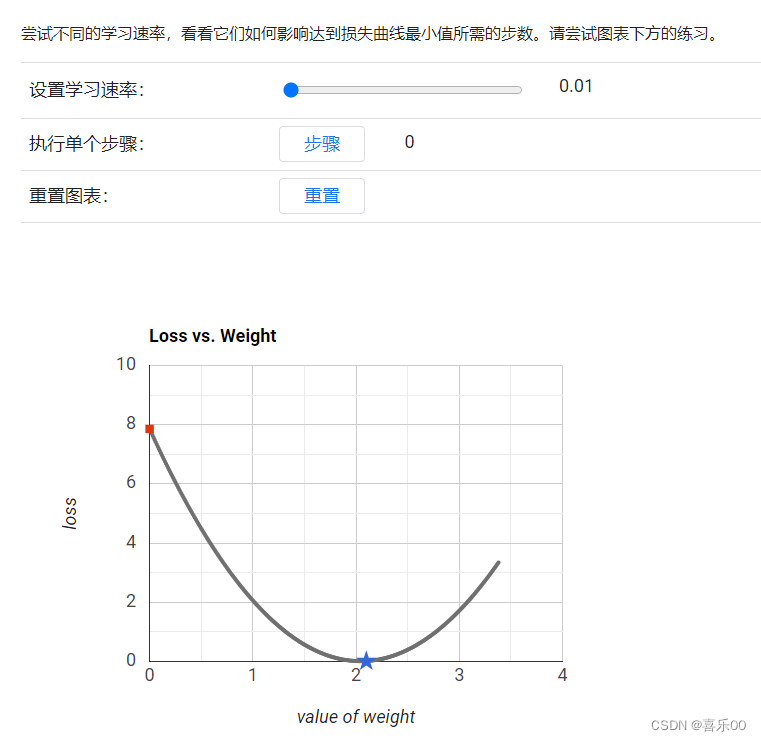
谷歌学习平台提供了： 尝试不同的学习速率，看看它们如何影响达到损失曲线最小值所需的步数。
https://developers.google.cn/machine-learning/crash-course/fitter/graph?hl=zh-c

5.降低损失 (Reducing Loss)：随机梯度下降法

在梯度下降法中，批次是用于在单次训练迭代中计算梯度的一组样本。 Google 数据集通常包含大量特征。因此，一个批次可能非常庞大。超大的批量也可能会导致单次迭代就可能需要很长时间才能完成计算。

具有随机抽样样本的大型数据集可能包含冗余数据。事实上，随着批次大小的增加，冗余的可能性会越来越高。一些冗余可能有助于消除嘈杂的梯度，但与大批量相比，大量的批量往往具有更高的预测价值。

如果我们可以通过更少的计算量得出正确的平均梯度，会怎么样？通过从数据集内随机选择样本，我们可以从小得多的样本中估算出大的平均值（尽管会有噪声）。 随机梯度下降法 (SGD) 将这种想法运用到极致，它每次迭代只使用一个样本（批次大小为 1）。如果有足够的迭代，SGD 可以正常工作，但噪声非常嘈杂。术语“随机”表示构成每个批次的一个样本是随机选择的。

小批量随机梯度下降法（小批量 SGD）是介于全批量迭代与 SGD 之间的折衷方案。小批次通常包含 10 到 1,000 个随机选择的样本。小批量 SGD 可以减少 SGD 中的噪声数，但仍然比全批量更高效。

5.1 补充：Goldilocks Principle 金发女孩原则

Goldilocks
(usually initial capital) Not being extreme or not varying drastically between extremes, especially between hot and cold.
Goldilocks Principle = Just the right amount = 刚刚好

西方有这么一个儿童故事叫 “ The Three Bears（金发女孩与三只小熊）”，迷路了的金发姑娘未经允许就进入了熊的房子，她尝了三只碗里的粥，试了三把椅子，又在三张床上躺了躺。最后发现不烫不冷的粥最可口，不大不小的椅子坐着最舒服，不高不矮的床上躺着最惬意。道理很简单，刚刚好就是最适合的，just the right amount，这样做选择的原则被称为 Goldilocks principle（金发女孩原则）。

金发姑娘原则不仅适用于日常生活中的决策，也被广泛应用于多个领域，如发展心理学、经济学、通讯科学、医学和天体生物学等。在个人发展和人际关系方面，这个原则鼓励人们寻找平衡点，避免走向极端，从而更有效地解决问题和建立和谐的关系。

在天体宇宙学中，Goldilocks Zone是最适合居住的环境，温度上不过热不过冷，正正好适宜生命的成长，地球就是最典型的Goldilocks Planet。
在经济学中，Goldilocks economy 描述的经济状态不会太热导致通货膨胀，也不太冷导致经济萧条。这种正正好的状态下经济稳定，货币政策有利于市场，就业率也往往较高。