一、莱昂纳多·斐波那契（Leonardo Fibonacci）

斐波那契公元1170年生于意大利比萨，卒于1250年，被人称作“比萨的莱昂纳多”，是一名闻名于欧洲的数学家，其主要的著作有《算盘书》、《实用几何》和《四艺经》等。1202年，他撰写了《算盘全书》（Liber Abacci）一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。他的父亲被比萨的一家商业团体聘任为外交领事，派驻地点于阿尔及利亚地区，莱昂纳多因此得以在一个阿拉伯老师的指导下研究数学。他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地研究数学。

二、斐波那契数列（Fibonacci Sequence）

在1202年斐波那契提出了一个非常著名的数列，即：

假设一对兔子每隔一个月生一对一雌一雄的小兔子，每对小兔子在两个月以后也开始生一对一雌一雄的小兔子，每月一次，如此下去。年初时兔房里放一对大兔子，问一年以后，兔房内共有多少对兔子？
 

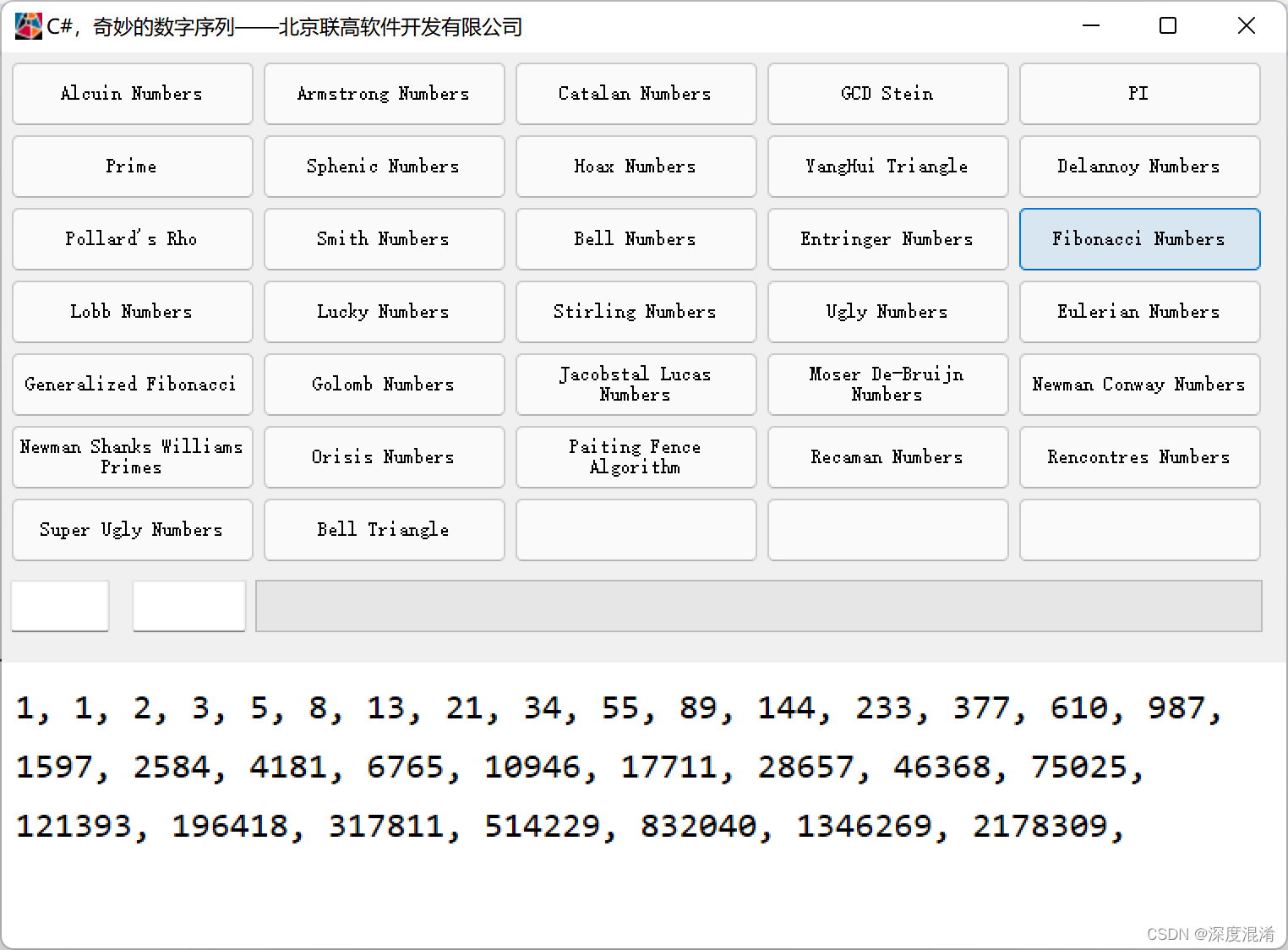
斐波那契数列（Fibonacci Sequence）指的是这样一个数列：1，1，2，3，5，8，13，21，34，55，89...，数列从第3项开始，每一项都等于前两项之和。

斐波那契数列由意大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci）定义。

斐波那契数列（Fibonacci Sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

三、斐波那契数列的算法

公式：

F(n)=F(n−1)+F(n−2)

计算结果：

 源程序：

using System;

namespace Legalsoft.Truffer.Algorithm
{
	public static partial class Number_Sequence
	{
		/// <summary>
		/// 斐波那契数列的原始（递归）算法
		/// </summary>
		/// <param name="n"></param>
		/// <returns></returns>
		public static int Fibonacci_Number(int n)
		{
			if (n <= 1)
			{
				return n;
			}
			else
			{
				return Fibonacci_Number(n - 1) + Fibonacci_Number(n - 2);
			}
		}

		/// <summary>
		/// 斐波那契数列的改进（非递归）算法
		/// </summary>
		/// <param name="n"></param>
		/// <returns></returns>
		public static int Fibonacci_Number_Second(int n)
		{
			int[] f = new int[n + 2];
			f[0] = 0;
			f[1] = 1;
			for (int i = 2; i <= n; i++)
			{
				f[i] = f[i - 1] + f[i - 2];
			}
			return f[n];
		}

		/// <summary>
		/// 斐波那契数列的改进（非递归）算法
		/// </summary>
		/// <param name="n"></param>
		/// <returns></returns>
		public static int Fibonacci_Number_Third(int n)
		{
			if (n <= 0)
			{
				return 0;
			}
			int a = 0;
			int b = 1;
			for (int i = 2; i <= n; i++)
			{
				int c = a + b;
				a = b;
				b = c;
			}
			return b;
		}

		/// <summary>
		/// 斐波那契数列的改进（非递归）算法
		/// </summary>
		/// <param name="n"></param>
		/// <returns></returns>
		public static int Fibonacci_Number_Fourth(int n)
		{
			int[,] F = new int[2, 2] { { 1, 1 }, { 1, 0 } };
			if (n <= 0)
			{
				return 0;
			}
			Fib4_Power(ref F, n - 1);
			return F[0, 0];
		}

		/// <summary>
		/// 2x2矩阵乘法
		/// </summary>
		/// <param name="F"></param>
		/// <param name="M"></param>
		static void Fib_Multiply(ref int[,] F, int[,] M)
		{
			int x = F[0, 0] * M[0, 0] + F[0, 1] * M[1, 0];
			int y = F[0, 0] * M[0, 1] + F[0, 1] * M[1, 1];
			int z = F[1, 0] * M[0, 0] + F[1, 1] * M[1, 0];
			int w = F[1, 0] * M[0, 1] + F[1, 1] * M[1, 1];

			F[0, 0] = x;
			F[0, 1] = y;
			F[1, 0] = z;
			F[1, 1] = w;
		}

		/// <summary>
		/// 求幂
		/// </summary>
		/// <param name="F"></param>
		/// <param name="n"></param>
		static void Fib4_Power(ref int[,] F, int n)
		{
			int[,] M = new int[2, 2] { { 1, 1 }, { 1, 0 } };
			for (int i = 2; i <= n; i++)
			{
				Fib_Multiply(ref F, M);
			}
		}

		/// <summary>
		/// 斐波那契数列的改进（非递归）算法
		/// </summary>
		/// <param name="n"></param>
		/// <returns></returns>
		public static int Fibonacci_Number_Fifth(int n)
		{
			if (n <= 0)
			{
				return 0;
			}
			int[,] F = new int[2, 2] { { 1, 1 }, { 1, 0 } };
			Fib5_Power(ref F, n - 1);
			return F[0, 0];
		}

		/// <summary>
		/// 求幂方法的改进
		/// </summary>
		/// <param name="F"></param>
		/// <param name="n"></param>
		private static void Fib5_Power(ref int[,] F, int n)
		{
			if (n == 0 || n == 1)
			{
				return;
			}
			int[,] M = new int[,] { { 1, 1 }, { 1, 0 } };
			Fib5_Power(ref F, n / 2);
			Fib_Multiply(ref F, F);
			if (n % 2 != 0)
			{
				Fib_Multiply(ref F, M);
			}
		}

		private static int MAX { get; set; } = 1000;
		private static int[] pool { get; set; } = null;

		/// <summary>
		/// 斐波那契数列的改进（非递归）算法
		/// </summary>
		/// <param name="n"></param>
		/// <returns></returns>
		public static int Fibonacci_Number_Sixth(int n)
		{
			if (pool == null)
			{
				pool = new int[MAX];
			}
			if (n <= 0)
			{
				return 0;
			}
			if (n == 1 || n == 2)
			{
				return (pool[n] = 1);
			}
			if (pool[n] != 0)
			{
				return pool[n];
			}
			int k = ((n & 1) == 1) ? ((n + 1) / 2) : (n / 2);
			int k1 = Fibonacci_Number_Sixth(k - 1);
			int k2 = Fibonacci_Number_Sixth(k);
			int b1 = (k2 * k2 + k1 * k1);
			int b2 = (2 * k1 + k2) * k2;
			pool[n] = ((n & 1) == 1) ? b1 : b2;
			//f[n] = (n & 1) == 1 ? (fib(k) * fib(k) +
			//				   fib(k - 1) * fib(k - 1))
			//				   : (2 * fib(k - 1) + fib(k)) *
			//									   fib(k);
			return pool[n];
		}

		/// <summary>
		/// 斐波那契数列的改进（非递归）算法
		/// </summary>
		/// <param name="n"></param>
		/// <returns></returns>
		public static int Fibonacci_Number_Seventh(int n)
		{
			double phi = (1 + Math.Sqrt(5)) / 2;
			return (int)Math.Round(Math.Pow(phi, n) / Math.Sqrt(5));
		}

		/// <summary>
		/// 斐波那契数列的改进（非递归）算法
		/// </summary>
		/// <param name="n"></param>
		/// <returns></returns>
		public static int Fibonacci_Number_Eighth(int n)
		{
			if (pool == null)
			{
				pool = new int[MAX];
			}
			if (n <= 1)
			{
				return n;
			}
			int first;
			int second;
			if (pool[n - 1] != -1)
			{
				first = pool[n - 1];
			}
			else
			{
				first = Fibonacci_Number_Eighth(n - 1);
			}
			if (pool[n - 2] != -1)
			{
				second = pool[n - 2];
			}
			else
			{
				second = Fibonacci_Number_Eighth(n - 2);
			}
			pool[n] = first + second;
			return pool[n];
		}
	}
}

——————————————————————————

POWER  BY  TRUFFER.CN