257. 二叉树的所有路径
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
示例 2:
输入:root = [1] 输出:["1"]
思路:递归,结束条件是一个结点没有左孩子和右孩子。题目提示中写到至少会有一个根节点,那么不用判断树空的情况。
代码实现:
class Solution {
void generate(TreeNode *node, string path, vector<string> &result) {
path += to_string(node->val);
if(node->left && !node->left->left && !node->left->right) {
result.push_back(path);
return;
}
if(node->left) generate(node->left, path + "->", result);
if(node->right) generate(node->right, path + "->", result);
}
vector<string> binaryTreePaths(TreeNode* root) {
string path = "";
vector<string> result;
//if(!root) return result;
generate(root, path, result);
return result;
}
};404. 左叶子之和
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:

输入: root = [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1] 输出: 0
思路:递归,迭代都可以。迭代的话,前中后续都可行,下面的代码是后序遍历,注意判断左叶子结点即可。递归的判定条件也是相同的。
代码实现1:迭代
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
stack<TreeNode *> stk;
if(!root) return 0;
stk.push(root);
int ret = 0;
TreeNode *node;
while(!stk.empty()) {
node = stk.top();
stk.pop();
if(node->left && !node->left->left && !node->left->right) ret += node->left->val;
if(node->left) stk.push(node->left);
if(node->right) stk.push(node->right);
}
return ret;
}
};代码实现2:递归
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if(!root) return 0;
int leftValue = 0;
if(root->left && !root->left->left && !root->left->right) {
leftValue = root->left->val;
}
return leftValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
}
};
112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
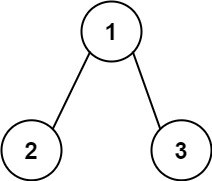
输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0 输出:false 解释:由于树是空的,所以不存在根节点到叶子节点的路径。
思路:递归+回溯,当得到的结果不满足时,需要往回退一步,寻找新的可能满足需求的路径。
代码实现:
class Solution {
public:
bool calculate(TreeNode *node, int count) {
if(!node->left && !node->right && count == 0) return true;
if(!node->left && !node->right) return false;
if(node->left) {
count -= node->left->val;
if(calculate(node->left, count)) return true;
count += node->left->val;
}
if(node->right) {
count -= node->right->val;
if(calculate(node->right, count)) return true;
count += node->right->val;
}
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root) return false;
return calculate(root, targetSum - root->val);
}
};