每日一练：LeeCode-404、左叶子之和【二叉树】

news2024/9/22 9:44:18

本文是力扣LeeCode-404、左叶子之和 学习与理解过程，本文仅做学习之用，对本题感兴趣的小伙伴可以出门左拐LeeCode。

404、左叶子之和
给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：
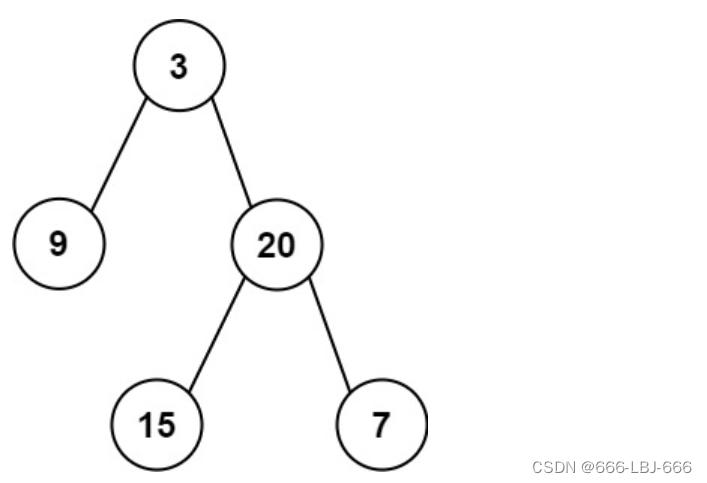
在这里插入图片描述

输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

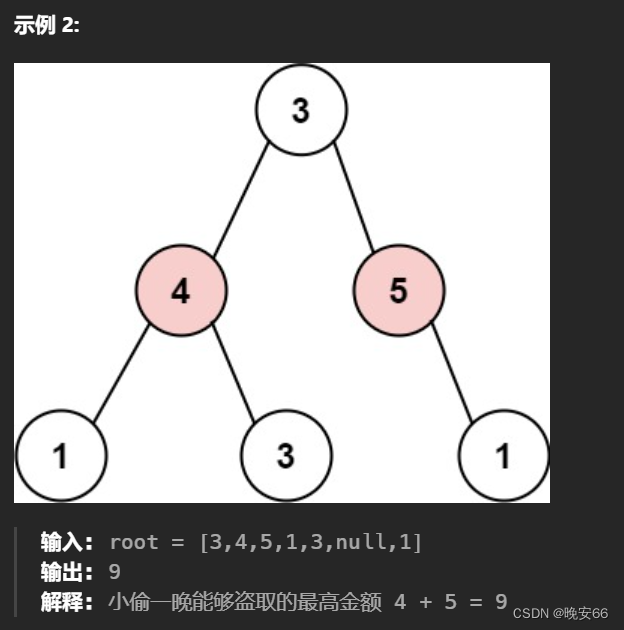
示例 2:

输入: root = [1]
输出: 0

提示:

节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000

思路

⾸先要注意是判断左叶⼦，不是⼆叉树左侧节点，所以不要上来想着层序遍历

左叶⼦的明确定义：节点A的左孩⼦不为空，且左孩⼦的左右孩⼦都为空（说明是叶⼦节点），那么A节点的左孩⼦为左叶⼦节点

直接判断当前节点是不是左叶⼦是不可能的，必须要通过节点的⽗节点来判断其左孩⼦是不是左叶⼦

递归法

本题采用后序遍历（左右中）是最好的，是因为要通过递归函数的返回值来累加求取左叶⼦数值之和

1、确定递归函数的参数和返回值

int sumOfLeftLeaves(TreeNode root)

2、确定终⽌条件
如果遍历到空节点，那么左叶⼦值⼀定是0

if(root==null)return 0;

3、确定单层递归的逻辑
当遇到左叶⼦节点的时候，记录数值，然后通过递归求取左⼦树左叶⼦之和，和 右⼦树左叶⼦之和，相加便是整个树的左叶⼦之和。

        int leftSum = sumOfLeftLeaves(root.left);
        //当前节点的左节点不为空，且该左节点的左右节点为空，则为左叶⼦节点的情况
        if(root.left!=null&&root.left.left==null&&root.left.right==null){
            leftSum+=root.left.val;
        }
        int rightSum = sumOfLeftLeaves(root.right);
        int sum = leftSum+rightSum;
        return sum;

完整代码

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root==null)return 0;
        int leftSum = sumOfLeftLeaves(root.left);
        if(root.left!=null&&root.left.left==null&&root.left.right==null){
            leftSum+=root.left.val;
        }
        int rightSum = sumOfLeftLeaves(root.right);
        int sum = leftSum+rightSum;
        return sum;
    }
}