数据分析讲课笔记02：科学计算库Numpy

文章目录

零、学习目标
一、认识NumPy数组对象
- （一）N维数组对象ndarray
- （二）ndarray对象重要的属性
- （三）ndarray数组案例演示
二、创建NumPy数组
- （一）采用array()函数创建数组
- （二）采用zeros()和ones()函数创建数组
- （三）采用empty()函数创建数组
- （四）采用arange()函数创建数组
- （五）注意事项
三、ndarray对象的数据类型
- （一）查看数据类型
- - 1、查看数据类型名
  - 2、数据类型的构成
  - 3、常用的数据类型
  - 4、数据类型的特征码
- （二）转换数据类型
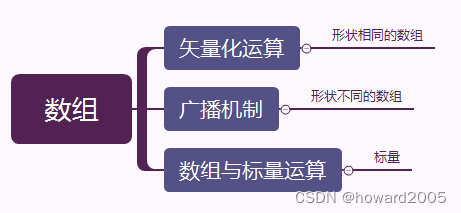
四、数组运算
- （一）矢量化运算
- （二）广播机制
- - 1、广播机制出现的场景
  - 2、广播机制满足的条件
- （三）数组与标量运算
五、ndarray的索引和切片
- （一）整数索引和切片的基本使用
- - 1、针对一维数组
  - 2、针对二维数组
- （二）花式（数组）索引的基本使用
- （三）布尔型索引的基本使用
六、数组的转置和轴对称
- （一）使用T属性实现数组的转置
- （二）使用transpose()方法实现数组的转置
- （三）使用swapaxes()方法实现数组的转置
- （四）多学一招 - 维度编号问题
七、NumPy通用函数
- （一）通用函数概念
- （二）常见一元通用函数
- （三）常见二元通用函数
八、利用NumPy数组进行数据处理
- （一）将条件逻辑转为数组运算
- （二）数组统计运算
- （三）数组排序
- （四）检索数组元素
- （五）唯一化及其他集合逻辑
九、线性代数模块
- （一）线性代数模块
- （二）案例 - 求解线性方程组
- - 1、利用行列式计算
  - 2、利用矩阵计算
十、随机数模块
- （一）rand()函数
- （二）其它函数
十一、本节小结

零、学习目标

掌握创建数组，数组运算，索引与切片
掌握利用数组进行数据处理
掌握转置和轴对称，通用函数
熟悉数据类型，线性代数模块，随机数模块

NumPy是Python中用于数值计算的核心库，其中ndarray（n维数组）为其主要数据结构，提供高效存储和处理多维数据的能力。通过array()函数、zeros()、ones()等方法创建数组，并可指定数据类型如int32或float64。数组支持矢量化运算、广播机制以及与标量运算，简化了大量数学计算操作。利用索引和切片技术可以访问和修改数组元素，包括整数索引、切片索引、花式索引和布尔型索引。此外，NumPy提供了转置、轴对称变换以及通用函数如sum()、mean()等进行统计计算，还有排序、唯一化及集合逻辑操作。其linalg模块涵盖了线性代数相关功能，如矩阵乘法、求逆、解方程组等。随机数生成方面，random模块可产生各种概率分布的随机数，助力模拟实验和数据分析。

一、认识NumPy数组对象

（一）N维数组对象ndarray

NumPy库的核心功能体现在其N维数组对象ndarray上，该对象在Python中被广泛用于高效科学计算和数据分析。ndarray是一个多维数据结构，能够容纳同类型元素的集合，并且支持向量化运算、广播机制以及丰富的数学函数操作。通过定义如维度（ndim）、形状（shape）、大小（size）和数据类型（dtype）等关键属性，ndarray能够精确描述和控制大规模数值数据集。用户可通过多种方式创建数组，包括从列表、元组或特定值填充，并能灵活指定数据类型以满足不同精度需求。这些特性使得ndarray成为现代科学计算、机器学习和数据分析等领域不可或缺的基础工具。

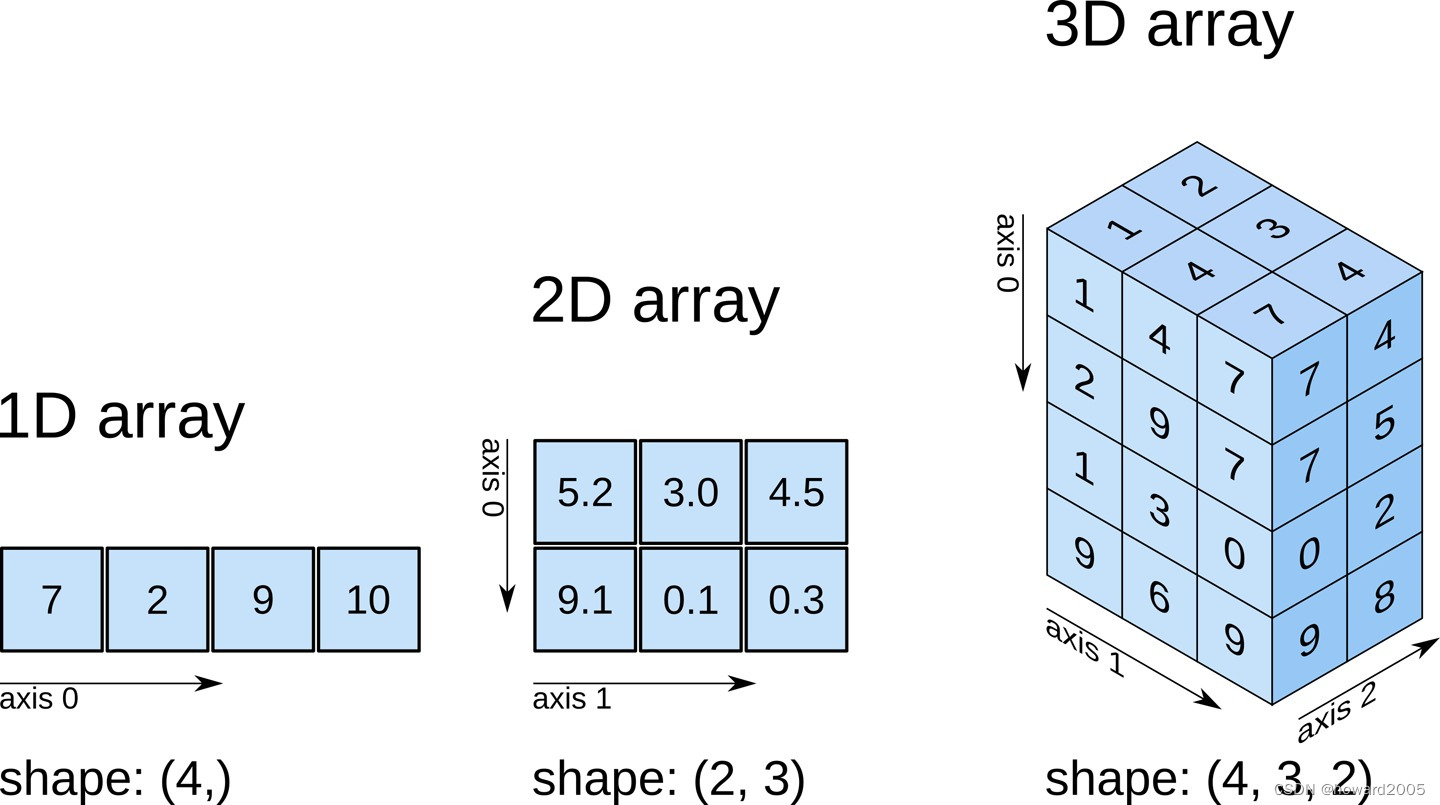
（二）ndarray对象重要的属性

属性	具体说明
ndarray	维度个数，也就是数组轴的个数，比知如一维、二维、三维等
ndarray.shape	数组的维度。这是一个整数的元组，表示每个维度上数组的大小。例如，一个n行和m列的数组，它的shape属性为(n, m)
ndarray.size	数组元素的总个数，等于shape属性中元组元素的乘积
ndarray.dtype	描述数组中元素类型的对象，既可以使用标准的Python类型创建或指定，也可以使用NumPy特有的数据类型来指定，比如numpy.int32、numpy.float64等
ndarray.itemsize	数组中每个元素的字节大小。例如，元素类型为float64的数组有8 ( 64/8）个字节，这相当于ndarray.dtype.itemsize

（三）ndarray数组案例演示

创建数组（3行4列的二维数组）
查看变量数据类型
查看数组对象属性

二、创建NumPy数组

NumPy库中创建ndarray对象有多种方式。首先，使用array()函数将列表或元组转换为数组。其次，zeros()和ones()分别生成元素全为0或1的数组，而empty()则创建一个未初始化（随机填充）的数组。另外，通过arange()可以创建等差数列组成的数组，类似Python内置的range()但返回结果是数组类型。最后，注意数组中的元素显示形式，如1与1.的区别源于元素的数据类型差异。

（一）采用array()函数创建数组

最简单的创建ndarray对象的方式是使用array()函数，在调用该函数时传入一个列表或者元组。

（二）采用zeros()和ones()函数创建数组

通过zeros()函数创建元素值都是0的数组；通过ones()函数创建元素值都为1的数组。

（三）采用empty()函数创建数组

通过empty()函数创建一个新的数组，该数组只分配了内存空间，它里面填充的元素都是随机的。

（四）采用arange()函数创建数组

通过arange()函数可以创建一个等差数组，它的功能类似于range()，只不过arange()函数返回的结果是数组，而不是列表。

（五）注意事项

大家可能注意到，有些数组元素的后面会跟着一个小数点，而有些元素后面没有，比如1和1.，产生这种现象，主要是因为元素的数据类型不同所导致的。

三、ndarray对象的数据类型

NumPy的ndarray对象具有特定的数据类型，通过ndarray.dtype.name可查看具体类型名称。数组创建时，默认如zeros、ones等函数生成float64类型数据，在不同系统上整数默认长度可能不同（int32或int64）。支持多种数据类型包括布尔、整型、浮点型、复数以及对象和字符串等，并可通过dtype参数指定。转换数据类型使用astype()方法，例如将整型数组转为浮点型。特征码提供了一种简写形式标识数据类型。

（一）查看数据类型

1、查看数据类型名

ndarray.dtype可以创建一个表示数据类型的对象，如果希望获取数据类型的名称，则需要访问name属性进行获取。

2、数据类型的构成

NumPy的数据类型是由一个类型名和元素位长的数字组成。

通过zeros()、ones()、empty()函数创建的数组，默认的数据类型为float64。
默认情况下，64位windows系统输出的结果为int32，64位Linux或macOS系统输出结果为int64，当然也可以通过dtype来指定数据类型的长度。

3、常用的数据类型

数据类型	含义
bool_	布尔类型，值为True或False
int8, uint8	有符号和无符号的8位整数
int16, uint16	有符号和无符号的16位整数
int32, uint32	有符号和无符号的32位整数
int64, uint64	有符号和无符号的64位整数
float16	半精度浮点数（16位）
float32	半精度浮点数（32位）
float64	半精度浮点数（64位）
complex64	复数，分别用两个32位浮点数表示实部和虚部
complex128	复数，分别用两个64位浮点数表示实部和虚部
object	Python对象
stirng_	固定长度的字符串类型
uncode_, str_	固定长度的unicode类型

创建数组时不指定数据类型
创建数组时指定数据类型

4、数据类型的特征码

特征码	含义
b	布尔型
u	无符号整型
c	复数类型
S, a	字节字符串
V	原始数据
i	有符号整型
f	浮点型
O	Python对象
U	unicode字符串

（二）转换数据类型

ndarray对象的数据类型可以通过astype()方法进行转换。
创建二维整型数组
将整型转换成浮点型

四、数组运算

NumPy数组支持三种类型的运算：矢量化运算、广播机制和数组与标量运算。矢量化运算允许相同形状的数组进行元素级别的算术运算，生成新数组。广播机制在不同形状数组间运算时启用，自动扩展数组以匹配维度并逐元素计算。满足条件（相同维度长度或一维数组参与）时可进行广播。标量与数组运算会将标量值应用到数组所有元素上，产生同样形状的新数组。

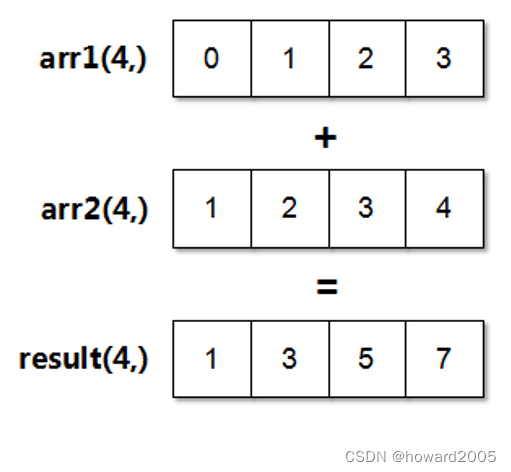
（一）矢量化运算

形状相等的数组之间的任何算术运算都会应用到元素级，即只用于位置相同的元素之间，所得的运算结果组成一个新的数组。
一维数组加法运算（逐个元素相加）
二维数组乘法运算（逐个元素相乘）

（二）广播机制

1、广播机制出现的场景

当形状不相等的数组执行算术计算的时候，就会出现广播机制，该机制会对数组进行扩展，使数组的shape属性值一样，这样就可以进行矢量化运算了。
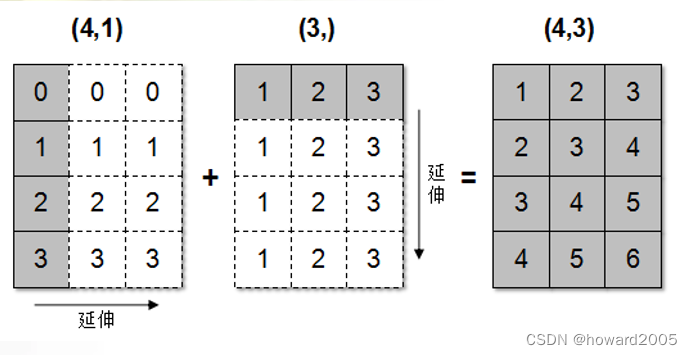
案例演示

2、广播机制满足的条件

广播机制进行数组运算时，要求满足以下条件之一：要么两个数组在某一维度上有相同长度，要么其中一个是单维度数组。为实现逐元素运算，广播会将较小维度的数组扩展到与较大数组相同的形状，确保二者可以进行兼容的元素级计算。

（三）数组与标量运算

标量运算会产生一个与数组具有相同行和列的新矩阵，其原始矩阵的每个元素都被相加、相减、相乘或者相除。
案例演示

五、ndarray的索引和切片

NumPy库中的ndarray支持整数索引和切片操作，与Python列表相似但功能更丰富。在一维数组中，通过单个或多个整数直接索引元素；在二维数组中，采用元组形式(行号, 列号)访问特定元素，而切片可按需选取部分行或列。此外，ndarray特有的花式索引允许使用整数数组或列表选择多处数据，并能混合使用整数索引和切片。布尔型索引则根据布尔数组选取对应为True的元素。这些灵活的索引方式极大地增强了对多维数组数据的操作能力。

（一）整数索引和切片的基本使用

1、针对一维数组

对于一维数组来说，从表面上来看，它使用索引和切片的方式，与Python列表的功能相差不大。

2、针对二维数组

对于多维数组来说，索引和切片的使用方式与列表就大不一样了
二维数组的索引方式如下所示
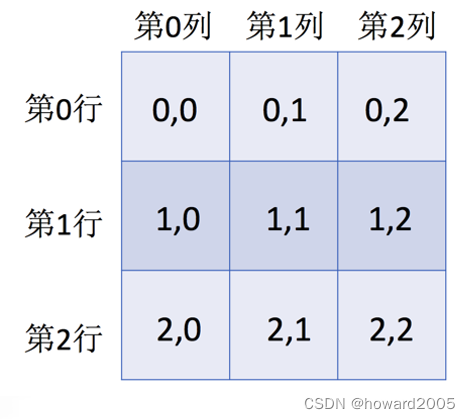
在二维数组中，每个索引位置上的元素不再是一个标量了，而是一个一维数组。
获取二维数组第1行数据
获取二维数组第2列数据
如果想获取二维数组的单个元素，则需要通过形如“arr[x，y]”的索引来实现，其中x表示行号，y表示列号。
多维数组的切片是沿着行或列的方向选取元素的，我们可以传入一个切片，也可以传入多个切片，还可以将切片与整数索引混合使用。

（二）花式（数组）索引的基本使用

花式索引是NumPy的一个术语，是指用整数数组或列表进行索引，然后再将数组或列表中的每个元素作为下标进行取值。
当使用一个数组或列表作为索引时，如果使用索引要操作的对象是一维数组，则获取的结果是对应下标的元素。
如果要操作的对象是一个二维数组，则获取的结果就是对应下标的一行数据。
获取索引为[0, 2]的元素
案例演示
如果用两个花式索引操作数组，则会将第1个作为行索引，第2个作为列索引，以二维数组索引的方式选取其对应位置的元素。
获取索引为(1, 1)和(3, 2)的元素

（三）布尔型索引的基本使用

布尔型索引指的是将一个布尔数组作为数组索引，返回的数据是布尔数组中True对应位置的值。

六、数组的转置和轴对称

NumPy中数组的转置操作可通过T属性或transpose()方法实现，其中T属性适用于简单转置（例如二维数组行列互换），而transpose()允许指定轴编号进行更复杂的维度变换，默认情况下执行常规转置。此外，针对特定两个轴交换需求，可使用swapaxes()方法。在处理高维数据时需注意，轴编号从0开始计数，依次对应各个维度，这在进行转置等操作时至关重要。

（一）使用T属性实现数组的转置

简单的转置可以使用T属性，它其实就是进行轴对换而已。

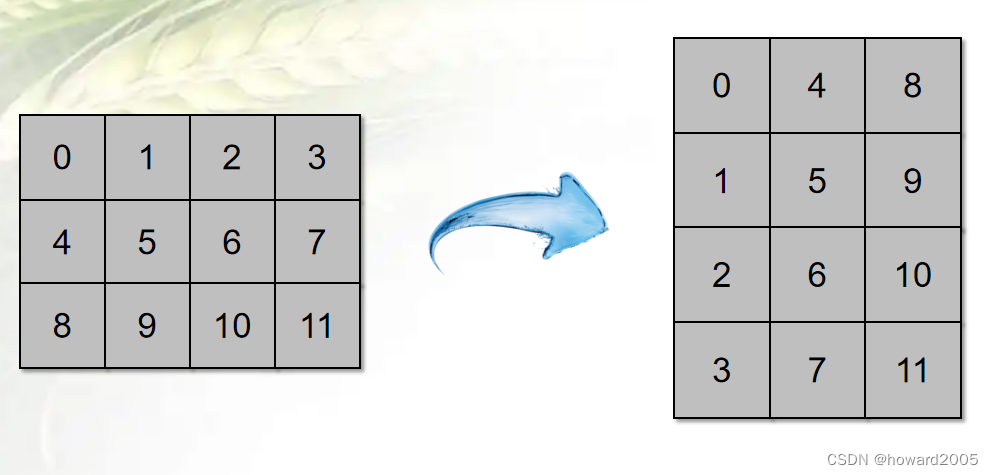
（二）使用transpose()方法实现数组的转置

当使用transpose()方法对数组的shape进行调换时，需要以元组的形式传入shape的编号，比如(1, 0, 2)。
如果我们不输入任何参数，直接调用transpose()方法，则其执行的效果就是将数组进行转置，作用等价于transpose(2, 1, 0)。

（三）使用swapaxes()方法实现数组的转置

有时可能只需要转换其中的两个轴，这时可以使用swapaxes()方法实现，该方法需要接受一对轴编号，比如(1,0)。

（四）多学一招 - 维度编号问题

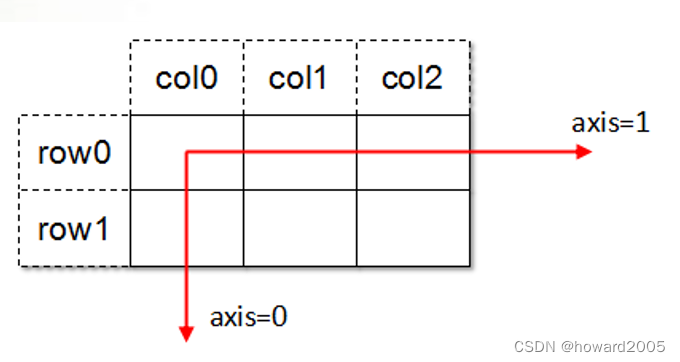
高维数据执行某些操作（如转置）时，需要指定维度编号，这个编号是从0开始的，然后依次递增1。其中，位于纵向的轴（y轴）的编号为0，位于横向的轴（x轴）的编号为1，以此类推。

七、NumPy通用函数

（一）通用函数概念

NumPy中的通用函数（ufuncs）是高效执行数组元素级运算的关键工具，包括一元和二元函数。一元ufunc如abs计算绝对值，sqrt求平方根等；二元ufunc如add进行元素级加法，subtract进行减法等。这些函数可处理整数、浮点数、复数及逻辑比较，并支持三角函数、指数对数运算以及判断无穷、NaN等特殊数值。通过运用ufunc，用户能轻松实现快速且向量化的基本数学运算。

（二）常见一元通用函数

函数	描述
abs, fabs	计算整数、浮点数或复数的绝对值
sqrt	计算各元素的平方根
exp	计算各元素的指数 $e^x$
log, log10, log2, log1p	分别为自然对数（底数为e），底数为10的log，底数为2的log，自然底数的log(1+x)
sign	计算各元素的正负号：1（正数）、0（零）、-1（负数）
ceil	计算各元素的ceiling值，即大于或者等于该值的最小整数
floor	计算各元素的floor值，即小于或者等于该值的最大整数
rint	将各元素四舍五入到最接近的整数
modf	将数组的小数和整数部分以两个独立数组的形式返回
isnan	返回一个表示“哪些值是NaN”的布尔型数组
isfinite, isinf	分别返回表示“哪些元素是有穷的”或“哪些元素是无穷”的布尔型数组
sin、sinh、cos、cosh、tan、tanh	普通型和双曲型三角函数
arcsin、arcsinh、arccos、arccosh、arctan、arctanh	普通型和双曲型反三角函数

案例演示

（三）常见二元通用函数

函数	描述
add	将数组中对应的元素相加
subtract	将数组中对应的元素相减
multiply	将数组中对应的元素相乘
divide, floor_divide	除法或向下整除法（舍去余数）
maximum, fmax	元素级的最大值计算
minimum, fmin	元素级的最小值计算
mod	元素级的求模运算
copysign	将第二个数组的值的符号赋值给第一个数组中的值
greater、greater_equal、less、less_equal、equal、not_equal、logical_and、logical_or、logical_not	执行元素级的比较运算，最终产生布尔型数组，相当于运算符>、≥、<、≤、==、!=

案例演示

八、利用NumPy数组进行数据处理

NumPy库为数组数据处理提供了丰富的方法。其中where()函数实现条件逻辑的向量化，进行元素级选择赋值。统计运算如求和、平均、最大最小值以及它们对应的索引等操作简单易行。数组排序可使用sort()方法，并指定轴参数对特定维度排序。通过all()和any()函数可快速判断数组内所有或任一元素是否满足条件。此外，NumPy还支持集合逻辑操作，如唯一化（unique()）、交集（intersect1d()）、并集（union1d()）和差集（setdiff1d()）等，便于高效处理集合关系。利用这些功能，用户能便捷地完成各类复杂的数据分析任务。

（一）将条件逻辑转为数组运算

NumPy的where()函数是三元表达式x if condition else y的矢量化版本。

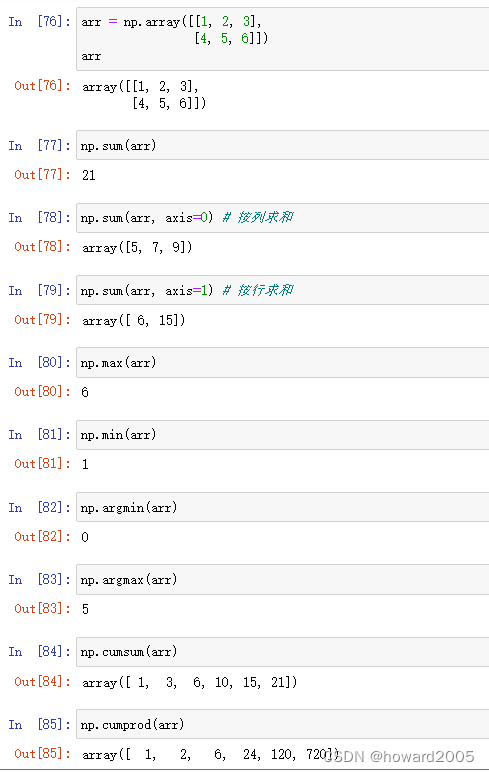
（二）数组统计运算

通过NumPy库中的相关方法，我们可以很方便地运用Python进行数组的统计汇总。

方法	描述
sum	对数组中全部或某个轴向的元素求和
mean	算术平均值
min	计算数组中的最小值
max	计算数组中的最大值
argmin	表示最小值的索引
argmax	表示最大值的索引
cumsum	所有元素的累计和
cumprod	所有元素的累计积

案例演示

（三）数组排序

如果希望对NumPy数组中的元素进行排序，可以通过sort()方法实现。
如果希望对任何一个轴上的元素进行排序，则需要将轴的编号作为sort()方法的参数传入。

（四）检索数组元素

all()函数用于判断整个数组中的元素的值是否全部满足条件，如果满足条件返回True，否则返回False。
any()函数用于判断整个数组中的元素至少有一个满足条件就返回True，否则就返回False。

（五）唯一化及其他集合逻辑

针对一维数组，NumPy提供了unique()函数来找出数组中的唯一值，并返回排序后的结果。
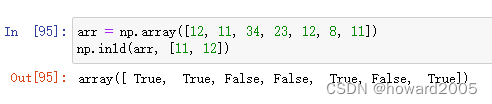
in1d()函数用于判断数组中的元素是否在另一个数组中存在，该函数返回的是一个布尔型的数组。
NumPy提供的有关集合的函数还有很多，常见的函数如下表所示。

函数	描述
unique(x)	计算x中的唯一元素，并返回有序结果
intersect1d(x, y)	计算x和y的交集，并返回有序结果
union1d(x, y)	计算x和y的并集，并返回有序结果
in1d(x, y)	得到一个表示“x的元素是否包含y”的布尔型数组
setdiff1d(x, y)	集合的差，即元素在x中且不在y中
setxor1d(x, y)	集合的对称差，即存在于一个数组中但不同时存在于两个数组中的元素

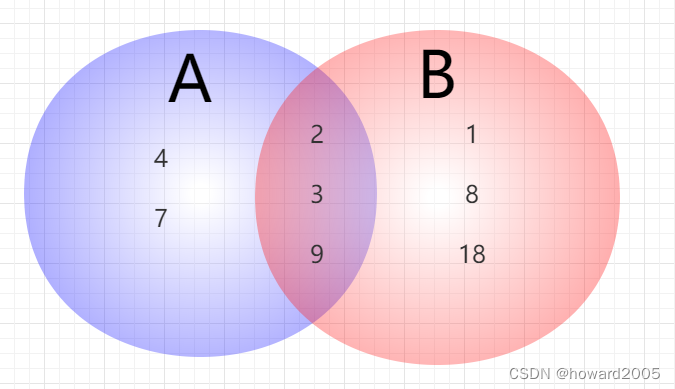
演示交、并、差、对称差运算
利用维恩图表示集合运算

九、线性代数模块

（一）线性代数模块

NumPy的numpy.linalg模块提供了丰富的线性代数运算，如矩阵乘法（dot函数）、计算行列式（det函数）、求逆矩阵（inv函数）、解线性方程组（solve函数）和进行矩阵分解等。利用这些函数，用户可以方便地解决复杂的数学问题。例如，在求解线性方程组时，既可以应用克莱姆法则通过计算行列式来求解变量，也可直接使用linalg.solve()方法实现高效精确计算。此外，该模块还支持对角线操作、迹计算以及特征值和奇异值分解等功能，满足不同场景下的矩阵分析需求。
例如，矩阵相乘，如果我们通过“*”对两个数组相乘的话，得到的是一个元素级的积，而不是一个矩阵点积。
NumPy中提供了一个用于矩阵乘法的dot()方法。
矩阵点积的条件是矩阵A的列数等于矩阵B的行数，假设A为 m*p的矩阵，B为 p*n 的矩阵，那么矩阵A与B的乘积就是一个 m*n 的矩阵C，其中矩阵C的第i行第j列的元素可以表示为：
$\cdot B=\displaystyle \sum_{k=1}^p a_{ik}b_{kj}=a_{i1}b_{1j}+a_{i2}b_{2j}+……+a_{ip}b_{pj}$
除此之外，linalg模块中还提供了其他很多有用的函数。

函数	描述
dot	矩阵乘法
diag	以一维数组的形式返回方阵的对角线，或将一维数组转为方阵
trace	计算对角线元素和
det	计算方阵的行列式
eig	计算方阵的特征值和特征向量
inv	计算方阵的逆
qr	计算qr分解
svd	计算奇异值
solve	解线性方程组AX=b，其中A是一个方阵
lstsq	计算AX=b的最小二乘解

（二）案例 - 求解线性方程组

$\begin{cases} x + 2y + 3z = 14 &(1)\\ 2x -4y +z = -3 &(2)\\ 3x + 5y - 2z = 7 &(3) \end{cases}$

1、利用行列式计算

$D=\left| \begin{matrix} 1 & 2 & 3\\ 2 & -4 & 1 \\ 3 & 5 & -2 \\ \end{matrix} \right|=83$

$D_1=\left| \begin{matrix} 14 & 2 & 3\\ -3 & -4 & 1 \\ 7 & 5 & -2 \\ \end{matrix} \right|=83$

$D_2=\left| \begin{matrix} 1 & 14 & 3\\ 2 & -3 & 1 \\ 3 & 7 & -2 \\ \end{matrix} \right|=166$

$D_3=\left| \begin{matrix} 1 & 2 & 14\\ 2 & -4 & -3 \\ 3 & 5 & 7 \\ \end{matrix} \right|=249$

据克莱姆法则得：
$x=\displaystyle \frac{D_1}{D}=\frac{83}{83}=1$
$y=\displaystyle \frac{D_2}{D}=\frac{166}{83}=2$
$z=\displaystyle \frac{D_3}{D}=\frac{249}{83}=3$
即 $\begin{cases} x=1\\ y=2\\ z=3 \end{cases}$

利用NumPy来计算

import numpy as np

D = np.linalg.det(np.matrix('1,2,3; 2,-4,1; 3,5,-2'))
D1 = np.linalg.det(np.matrix('14,2,3; -3,,-4,1; 7,5,-2'))
D2 = np.linalg.det(np.matrix('1,14,3; 2,-3,1; 3,7,-2'))
D3 = np.linalg.det(np.matrix('1,2,14; 2,-4,-3; 3,5,7'))

x = D1 / D
y = D2 / D
z = D3 / D

print('x = %.2f\ny = %.2f\nz = %.2f' %(x, y, z))

在这里插入图片描述

2、利用矩阵计算

$\left[ \begin{matrix} 1 & 2 & 3 \\ 2 & -4 & 1\\ 3 & 5 & -2 \\ \end{matrix} \right] \left[ \begin{matrix} x \\ y\\ z \\ \end{matrix} \right] =\left[ \begin{matrix} 14 \\ -3\\ 7 \\ \end{matrix} \right]$

$A=\left[ \begin{matrix} 1 & 2 & 3 \\ 2 & -4 & 1\\ 3 & 5 & -2 \\ \end{matrix} \right] ,X=\left[ \begin{matrix} x \\ y\\ z \\ \end{matrix} \right] ,B=\left[ \begin{matrix} 14 \\ -3\\ 7 \\ \end{matrix} \right]$

$AX=B\Longrightarrow X=A^{-1}B =\left[ \begin{matrix} 0.03614458 & 0.22891566 & 0.1686747 \\ 0.08433735 & -0.13253012 & 0.06024096\\ 0.26506024 & 0.01204819 & -0.09638554 \\ \end{matrix} \right] \left[ \begin{matrix} 14 \\ -3\\ 7 \\ \end{matrix} \right] =\left[ \begin{matrix} 1\\ 2\\ 3 \\ \end{matrix} \right]$

利用NumPy计算

import numpy as np

A = np.matrix('1,2,3; 2,-4,1; 3,5,-2')
B = np.matrix('14; -3; 7')
X = np.linalg.solve(A, B)

print('x = %.2f\ny = %.2f\nz = %.2f' %(X[0], X[1], X[2]))

在这里插入图片描述

十、随机数模块

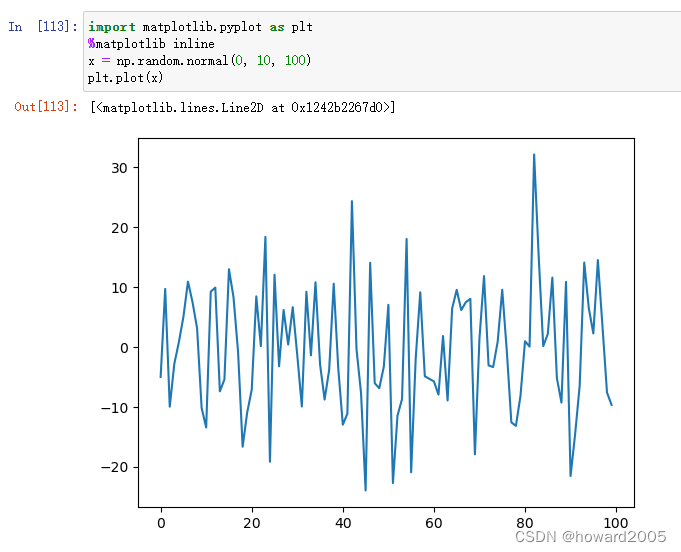
NumPy的numpy.random模块相较于Python内置的random模块，扩展了更多生成随机数的功能，尤其适用于高效创建满足多种概率分布样本的数组。rand()函数能够生成指定维度的均匀分布浮点数数组。此外，该模块包含一系列用于产生特定分布随机数的函数，如设定随机数生成起始点的seed()、生成均匀整数的randint()、模拟正态分布数据的normal()、遵循Beta分布的beta()以及在[0,1]区间内均匀分布的uniform()等。通过设置seed()可以确保随机数序列的可复现性，而不同参数或无参数调用时则会生成不同的随机数序列。例如，np.random.normal()可用于生成符合正态分布特性的数值样本，其参数分别控制均值、标准差和生成样本的数量。

（一）rand()函数

rand()函数隶属于numpy.random模块，它的作用是随机生成N维浮点数组。
随机生成一个二维数组

（二）其它函数

random模块中还包括了可以生成服从多种概率分布随机数的其它函数。

函数	描述
seed	生成随机数的种子
rand	产生均分分布的样本值
randint	从给定的上下限范围内随机选取整数
normal	产生正态分布的样本值
beta	产生Beta分布的样本值
uniform	产生在[0, 1]中的均匀分布的样本值

seed()函数可以保证生成的随机数具有可预测性，也就是说产生的随机数相同。

numpy.random.seed(seed=None)

上述函数中只有一个seed参数，用于指定随机数生成时所用算法开始的整数值。
当调用seed()函数时，如果传递给seed参数的值相同，则每次生成的随机数都是一样的。
当传递的参数值不同或者不传递参数时，则seed()函数的作用跟rand()函数相同，即多次生成随机数且每次生成的随机数都不同。
使用np.random.normal(mean, scale, size)可以生成很多数值呈正态分布数字。mean就是中间竖线的位置，scale就是横向挤压或拉伸程度，size是生成数字个数。