Focaler-IoU：更聚焦的IoU损失

摘要

边界框回归在目标检测领域中起着至关重要的作用，而目标检测的定位精度在很大程度上取决于边界框回归的损失函数。现有的研究通过利用边界框之间的几何关系来提高回归性能，而忽略了难易样本分布对边界框回归的影响。本文分析了难易样本分布对回归结果的影响，并提出了Focaler-IoU方法，该方法通过关注不同的回归样本，可以在不同的检测任务中提高检测器的性能。最后，通过使用现有的先进检测器和回归方法进行比较实验，进一步提高了使用本文提出的方法的检测性能。代码可在https://github.com/malagoutou/ Focaler-IoU上获取。

关键词：目标检测、损失函数、边界框回归

一、介绍

目标检测是计算机视觉的基本任务之一，其目的是在图像中定位和识别目标。根据是否生成锚点，可以将它们分为基于锚点和无锚点的方法。基于锚点的算法包括Faster R-CNN [1]、YOLO（You Only Look Once）系列 [2]、SSD（Single Shot MultiBox Detector） [3]和RetinaNet [4]。无锚点检测算法包括CornerNet [5]、CenterNet [6]和FCOS（Fully Convolutional One Stage Object Detection） [7]。在这些检测器中，边界框回归损失函数作为定位分支的重要组成部分，发挥着不可替代的作用。

A. 边界框回归损失

随着计算机视觉的发展，目标检测任务得到了研究人员的更多关注。为了评估各种算法在检测任务上的性能，需要引入适当的度量标准。在IoU（Intersection over Union） [8]被提出之前， l_{n} 范数损失 [13]被用作早期边界框回归问题的评估度量，然而，由于 l_{n} 范数损失对异常值非常敏感，这导致异常值对损失的影响更大，使得模型中存在异常值时性能不稳定。为了更好地解决上述问题，提出了一个更合适的度量标准：IoU（Intersection over Union） [8]。在基于IoU的评价准则下，大多数目标检测任务的检测精度得到了进一步提高，但IoU损失本身也存在一些缺点，例如，当GT框与锚点之间没有重叠时，它们的梯度会消失，这无法准确描述两个边界框之间的位置关系。为了弥补这一缺陷，GIoU [9]提出使用包含GT框和锚点的最小封闭框来计算损失可以提高检测性能。在CIoU和DIoU [10]中，为了弥补GIoU收敛速度慢的缺点，CIoU通过进一步考虑GT框与锚之间的宽高比来加速收敛，而DIoU通过归一化两个边界框质心之间的距离来加速收敛。EIoU [12]在CIoU的基础上进一步考虑了形状损失，通过最小化GT框与锚的宽度和高度之间的差异来加速收敛。SIoU [13]进一步考虑了连接两个边界框中心线的角度，并根据角度重新定义了距离损失和形状损失，并将其添加到损失函数中作为一个新的损失项，这使得基于IoU的当前损失函数达到了最佳的检测效果。

B. Focal Loss

在边缘回归过程中，训练样本不平衡的问题仍然存在。训练样本可以根据是否包含目标类别分为正样本和负样本。针对训练样本不平衡的一些传统解决方案是在训练过程中对困难样本进行采样和重新加权，然而，这种方法的效果并不显著。在Focal Loss [14]中，它提出容易识别的负样本在总损失中占主导地位，并主导梯度。Focal Loss [14]通过调整正负样本的权重，提高了模型识别稀有目标类别的能力，使模型更加关注难以分类的正样本，并减少相对容易分类的负样本的权重。在Libra R-CNN [15]中，提出了一种简单有效的平衡学习框架，其中在目标层使用平衡L1损失将训练样本分为离群点和内点。离群点被视为困难样本，与内点相比可以产生更大的梯度，这对训练过程是有害的。因此，Libra R-CNN使用梯度回归来促进内点并裁剪由离群点产生的较大梯度，以获得更好的分类结果。在EIoU [12]中，训练样本被分为高质量样本（锚点）和低质量样本（离群点），并在L1损失的基础上提出了FocalL1损失，以增加高质量样本对训练过程的梯度贡献。同时，将EIoU损失作为变量添加到FocalL1损失中，使模型能够更加关注高质量样本，以进一步提高检测效果。

本文的主要贡献如下：

我们分析了困难样本和易样本分布对边界框回归的影响。基于现有的边界框回归方法，我们提出了Focaler-IoU，通过线性区间映射来关注不同的回归样本。
我们使用先进的一阶段检测器进行了实验，验证了我们的方法可以有效提高检测性能，并弥补现有方法的不足之处。

II. 相关研究
近年来，随着检测器的发展，边缘回归损失得到了迅速发展。起初，IoU [8]被提出用于评估边界回归状态，然后基于IoU等，陆续提出了新的约束条件，如GIoU [9]，DIoU [10]，CIoU [10]，EIoU [12]和SIoU [11]等。

A. IoU度量

IoU（交集与并集之比）是最受欢迎的目标检测评估标准，其定义如下：
$U=\frac{\left|B \cap B^{g t}\right|}{\left|B \cup B^{g t}\right|}$
其中 B 和 B^{g t} 分别表示预测框和GT框。

B. GIoU度量

为了解决IoU损失在边界框回归中由于GT框和Anchor框之间无重叠而导致的梯度消失问题，提出了GIoU（通用交集与并集之比） [9]。其定义如下：
$U-\frac{\left|C-B \cap B^{g t}\right|}{|C|}$
其中 C 表示 GT 框和 Anchor 框之间的最小外接框。

C. DIoU度量

与GIoU相比，DIoU [10]考虑了边界框之间的距离约束，并在IoU的基础上添加了质心归一化距离损失项，从而使其回归结果更加准确。其定义如下：
$U-\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}}$

其中 b 和 b^{g t} 分别是锚框和GT框的中心点，\rho(\cdot) 表示欧几里得距离，其中 c 是 b 和 b^{g t} 之间的最小外接框的对角线距离。

CIoU [10]进一步通过在DIoU中添加新的形状损失项来考虑GT框和锚框之间的形状相似性，以减少锚框和GT框之间的纵横比差异。其定义如下：
$\begin{array}{c} C I o U=I o U-\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}}-\alpha v \\ \alpha=\frac{v}{(1-I o U)+v} \\ v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2} \end{array}$
其中 w^{g t} 和 h^{g t} 分别表示GT框的宽度和高度，w 和 h 分别表示锚框的宽度和高度。

D. EIoU度量

EIoU [12]重新定义了基于CIoU的形状损失，并通过直接减少GT框和锚框之间的纵横比差异，进一步提高了检测精度。其定义如下：

E I o U=I o U-\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{{2}}-\frac{\rho}{2}\left(w, w^{g t}\right)}{\left(w^{c}\right){2}}-\frac{\rho^{2}\left(h, h^{g t}\right)}{\left(h^{c}\right){2}}

其中 w^{c} 和 h^{c} 分别表示覆盖GT框和锚框的最小外接框的宽度和高度。

E. SIoU度量

在先前研究的基础上，SIoU [11]进一步考虑了边界框之间的角度对边界框回归的影响，旨在通过减小锚框和GT框之间的角度（水平或垂直方向）来加速收敛过程。其定义如下：
$\begin{array}{l} S I o U=I o U-\frac{(\Delta+\Omega)}{2} \\ \Lambda=\sin \left(2 \sin ^{-1} \frac{\min \left(\left|x_{c}^{g t}-x_{c}\right|,\left|y_{c}^{g t}-y_{c}\right|\right)}{\sqrt{\left(x_{c}^{g t}-x_{c}\right)^{2}+\left(y_{c}^{g t}-y_{c}\right)^{2}}+\epsilon}\right) \\ \Delta=\sum_{t=w, h}\left(1-e^{-\gamma \rho_{t}}\right), \gamma=2-\Lambda \\ \left\{\begin{array}{l} \rho_{x}=\left(\frac{x_{c}-x_{c}^{g t}}{w^{c}}\right)^{2} \\ \rho_{y}=\left(\frac{y_{c}-y_{c}^{g t}}{h^{c}}\right)^{2} \end{array}\right. \\ \Omega=\sum_{t=w, h}\left(1-e^{-\omega_{t}}\right)^{\theta}, \theta=4 \\ \left\{\begin{array}{l} \omega_{w}=\frac{\left|w-w_{g t}\right|}{\max \left(w, w_{g t}\right)} \\ \omega_{h}=\frac{\left|h-h_{g t}\right|}{\max \left(h, h_{g t}\right)} \end{array}\right. \\ \end{array}$

在这里插入图片描述

III. 方法
A. 分析

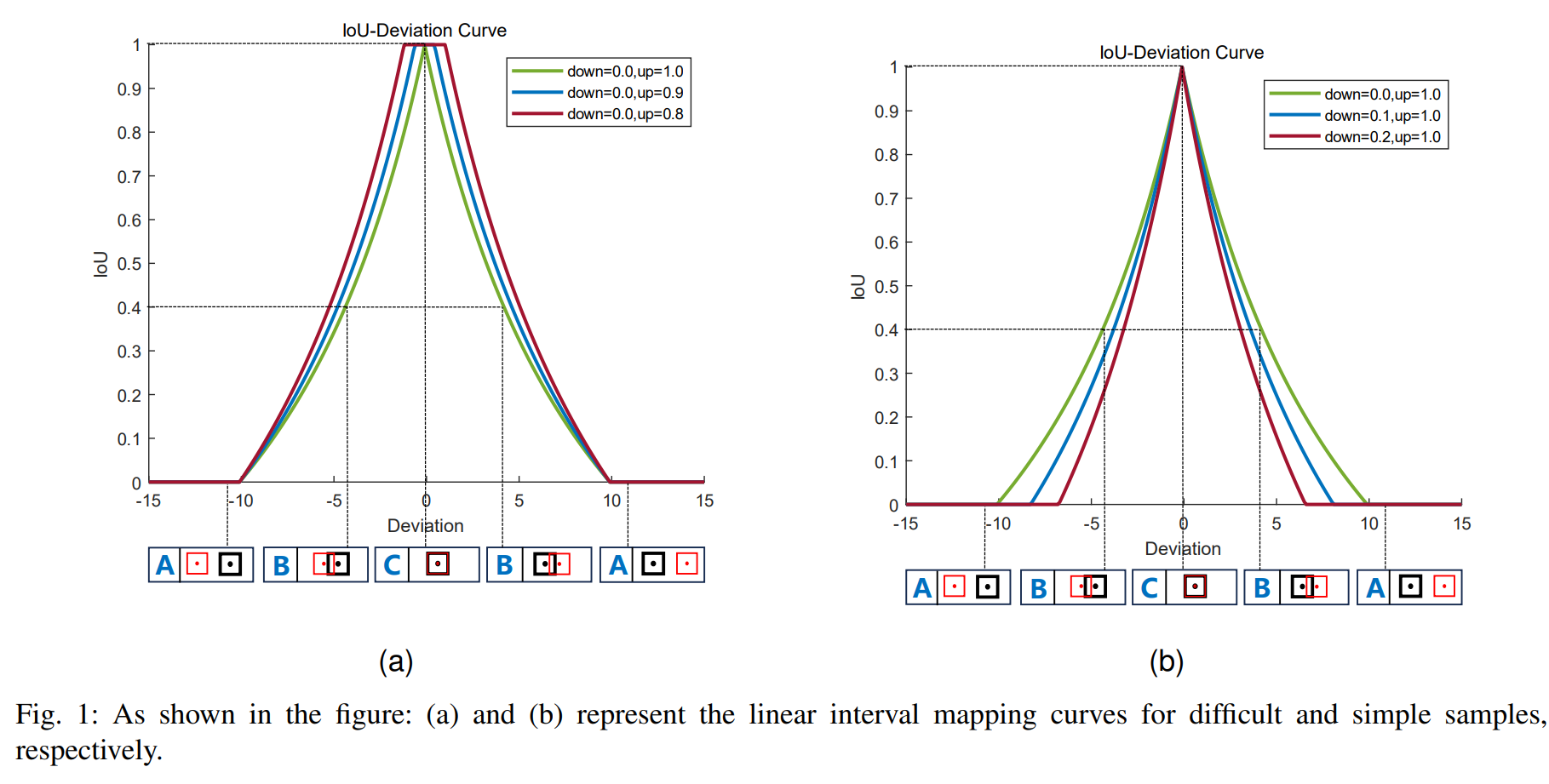
在各种目标检测任务中都存在样本不平衡的问题，根据目标检测的难度，可以将其分为困难样本和简单样本。从目标规模分析的角度来看，一般检测目标可以视为简单样本，而极小目标由于难以精确定位，可以视为困难样本。对于以简单样本为主的检测任务，在边界框回归过程中关注简单样本有助于提高检测性能。相反，对于困难样本比例较高的检测任务，需要关注困难样本的边界框回归。

B. Focaler-IoU

为了在不同的回归样本中关注不同的检测任务，我们使用线性间隔映射方法重构IoU损失，这有助于提高边缘回归。其公式如下：
$U^{\text {focaler }}=\left\{\begin{array}{ll} 0, & I o U<d \\ \frac{I o U-d}{u-d}, & d \ll I o U \ll u \\ 1, & I o U>u \end{array}\right.$

其中 I o U^{\text {focaler }} 是重构的Focaler-IoU，IoU是原始的IoU值，而 [d, u] \in[0,1] 。通过调整 d 和 u 的值，我们可以使 I o U^{\text {focaler }} 关注不同的回归样本。其损失定义如下：
$L_{\text {Focaler-IoU }}=1-I o U^{\text {focaler }}$
将Focaler-IoU损失应用于现有的基于IoU的边界框回归损失函数，L_{\text {Focaler-GIoU }}，L_{\text {Focaler-DIoU }}，L_{\text {Focaler-CIoU }}，L_{\text {Focaler-EIoU }}和L_{\text {Focaler-SIoU }}如下所示：

$\begin{array}{l} L_{\text {Focaler-GIoU }}=L_{G I o U}+I o U-I o U^{\text {Focaler }} \\ L_{\text {Focaler-DIoU }}=L_{D I o U}+I o U-I o U^{\text {Focaler }} \\ L_{\text {Focaler-CIoU }}=L_{C I o U}+I o U-I o U^{\text {Focaler }} \\ L_{\text {Focaler-EIoU }}=L_{E I o U}+I o U-I o U^{\text {Focaler }} \\ L_{\text {Focaler-SIoU }}=L_{S I o U}+I o U-I o U^{\text {Focaler }} \end{array}$

IV. 实验
A. YOLO v8 在PASCAL VOC上的实验

PASCAL VOC数据集是目标检测领域最受欢迎的数据集之一，本文使用VOC2007和VOC2012的训练和验证集作为训练集，包括16551张图像，并将VOC2007的测试集作为测试集，包含4952张图像。在本实验中，我们选择最先进的一阶检测器YOLOv8s和YOLOv7-tiny在VOC数据集上进行比较实验，选择SIoU作为实验的比较方法。实验结果如表I所示：
在这里插入图片描述

B. YOLOv5在AI-TOD上的实验

AI-TOD是一个遥感图像数据集，与一般数据集不同的是，它包含大量的小目标，目标的平均大小只有12.8像素。在本实验中，选择YOLOv5s作为检测器，比较方法为SIoU。实验结果如表II所示：
TABLE II: The performance of SIoU and Focaler-SIoU on Yolov5.