TOFU: A Two-Step Floorplan Refinement Framework
for Whitespace Reduction

摘要

平面规划作为实体设计的早期步骤，将极大地影响后期阶段的PPA。为了在保持相对相同的芯片尺寸的同时实现更好的性能，所生成的布图规划的利用率需要高，并且应当遵守与设计规则、可布线性、功率相关的约束。在本文中，我们提出了一个两步的框架，称为TOFU，平面图的空白减少固定轮廓和软/预置/硬模块建模。首先通过迭代地细化模块的位置来减少空白。然后，靠近空白的模块将被改变成直线形状，以进一步提高利用率。为了保证中间布图规划在精化过程中的合法性和质量，提出了一种基于约束图的合法化器和一种新的约束图构造方法。实验结果表明，Corblivar [1]生成的初始布图规划的空白平均可以减少约70%，在某些情况下可以减少高达90%。此外，由于更高的利用率，所得到的线长也缩短了3%。

一、简介

平面规划是现代建筑设计流程中最重要的环节之一。具有相同的芯片尺寸，具有更高利用率和更短线长的体面布图规划通常会导致具有更好功率、性能和面积（PPA）的更紧凑的设计。为了适应现实世界的物理实现需求，更多的约束已经被添加到经典的布局规划问题。如[2]中所述，具有预定轮廓的布图规划更实用，因为它能够为日益复杂的电路实现分层设计。此外，现代布图规划算法应该考虑预置模块（PPM）。经验表明，固定轮廓和预置模块约束会使算法更难产生具有高利用率和短互连的法律的布图规划[3]。因此，在这项工作中，我们将主要讨论实现具有固定轮廓和PPM的高利用率法律的布图规划。
近年来，[4]，[5]等分析方法已经显示出处理PPM的固定轮廓布图规划问题的良好潜力。经常使用两阶段流程，包括全局分配和合法化步骤。在全球分布阶段，模块将被分布在固定的轮廓，同时最大限度地减少总的线长。因此，通常存在模块重叠和越界模块，这些模块在合法化步骤中处理。Zhan等人[4]解决了一个无约束优化问题，以消除现有的模块重叠，并惩罚那些违反固定轮廓约束的模块。然而，随着大型硬模块的出现，他们的方法可能无法获得法律的布图规划。在文献[5]中，引入了一个推-拉模型，用于全局分布，其结果后来通过基于约束图的方法合法化。它们还明确地解决了PPM的存在，并利用直线形状来修复相关的重叠。然而，在他们提出的合法化步骤中，用于约束图提取的方法不够鲁棒，这可能（i）误解两个模块的相对位置或（ii）具有不受约束的节点对。这些因素可能导致模块之间的重叠和更长的线长。模块相对位置的误解将在第III-B节中具体讨论。最重要的是，上述作品都没有明确地将空白作为优化目标。
为了进一步提高利用率的初步布图，我们提出TOFU，一个有效的布图细化框架，是知道的固定轮廓和预置模块的限制。我们的贡献可归纳如下。

• 我们提出了一个两步框架的平面图空白删除与固定轮廓和预放置模块的限制意识。它可以用作任何布局规划方法的后处理步骤，以进一步提高其解决方案的利用率。
• 引入了一种鲁棒有效的约束图提取方法，以改进[5]中提到的方法。与原方法相比，我们可以更好地模拟两个模块的相对位置下的PPM，硬模块，超大型模块的存在。
• 针对不同的场景提出了两种方法来减少模块之间的空白。首先使用基于模块重定位的方法来解决初始解不佳和构建约束图时对相对位置的误解所导致的空白。然后，使用基于区域重新分配的方法来处理矩形形状无法去除的空白。

本文的其余部分组织如下。第二节介绍了一些与布图规划相关的方法，并定义了布图规划细化问题。第三节描述了我们提出的布局优化框架。第四节介绍了我们的实验设置和结果。第五节总结了我们的工作。

二、准备工作

2.1 布局规划

布图规划作为逻辑综合与物理设计之间的“桥梁”，一直是学术界研究的热点。给定网表和约束，布局规划问题用于确定模块的形状和位置，使得空白空间和线长最小化。请注意，可布线性可以通过具有接近零空白空间布局方案的馈通[6]来实现。在实践中，工程师还使用通道布线[7]，在允许的模块面积减少范围内在模块之间挖掘通道。布局规划中的约束可以分为以下类型。

• 模块属性约束：有三种类型的模块：（1）软模块，（2）硬模块，（3）预置模块（PPM）。对于软模块，形状和位置都可以改变，而对于硬模块，只能改变位置。至于PPM，它们的形状和位置应该保持不变。
• 固定轮廓约束：固定轮廓是一个直线区域，其中模块只能放置在内部。这种约束通常用于分层设计中，其中模块应该留在其父层次结构中的模块的边界内。

布局优化，类似于布局问题中的详细布局，对现代布局规划流程至关重要。不同的布图规划细化方法也可以很容易地用作任何布图规划方法的插件，以进一步提高质量或消除约束违反。

2.2 基于约束图的合法化

给定矩形形状（模块、单元、设备等）的初始放置，合法化问题是确定每个矩形的高度、宽度和位置，使得不存在约束违反并且目标度量被优化。给定的合法化输入为通常被认为是接近法律的解决方案。因此，矩形之间的相对位置应该被尊重，并且通常使用基于约束图的合法化来实现这一点。一个约束图包括两个有向无环图，记为$G_v$和$G_h$。图中的每个节点$n_i$表示第$i$个矩形$m_i$和一条从节点$n_i$到节点$n_j$的边$e_{ij}\in G_h(e_{ij}\in G_v)$表示$m_j$应该在$m_i$的右边（底部）。合法化可用公式表示：

其中，$x_i$,$y_i$,$w_i$,$h_i$和$a_i$分别表示第i个矩形的左下角坐标、宽度、高度和面积。

3 提出的算法

A 概况

如图1所示，我们的算法由三个部分组成：（1）平面图合法化，（2）基于模块位置的空白删除，以及（3）基于区域重新分配的空白删除。在第一步中，提出了一种基于约束图的布图合法化方法，以确保满足所有约束，提高利用率。在整个算法过程中，它将被多次调用。在第二步中，调整空白附近的模块的位置，以处理由模块的初始位置引起的空白。在第三步中，从底部区域开始，模块将从矩形变为直线形状以填充空白。我们的合法化方法和空白删除框架的细节将分别在第III-B节和第III-C节中讨论。

B 平面图合法化

在平面图合法化过程中，我们需要确定每个模块的形状和位置，以便满足所有约束。使用第II-B节中提到的基于约束图的方法，公式如下。

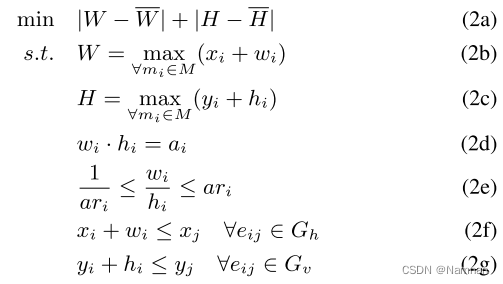
其中，$x_i$,$y_i$,$w_i$,$h_i$和$a_i$，$a{r}_i$分别表示第i个矩形的左下角坐标、宽度、高度和面积和最大纵横比。轮廓的宽度和高度由（W，H）表示。目标是最小化实际轮廓（W，H）和固定轮廓（W，H）之间的差异。实际轮廓由每个模块的右上角确定，如等式（2b）和（2c）所示。模块面积和纵横比的约束在等式（2d）和（2 e）中建模。最后，等式（2f）和（2g）确保只要适当地构建约束图，就不存在模块重叠。我们的约束图构造方法的细节将在下面的部分中介绍。注意，与[5]不同，我们在求解方程（2）时固定PPM的位置/形状和硬模块的形状。方程（2）可以通过二阶锥规划（SOCP）[5]或拉格朗日松弛[8]求解。在我们的实现中，为了便于集成，我们使用Guidance [9]将方程作为SOCP问题求解。

1）约束图构造：

我们的约束图（CG）构造方法是基于[5]中提到的方法。首先，使用Delaunay三角剖分（DT）方法来找到模块之间的相邻信息。$DT$图中连接的任何两个节点表示彼此相邻的两个模块。将在$G_v$或$G_h$中构造一条边来表示它们的相对位置。然而，[5]中从$DT$图构造$CG$的方法有两个主要缺点，如第I节所讨论的。

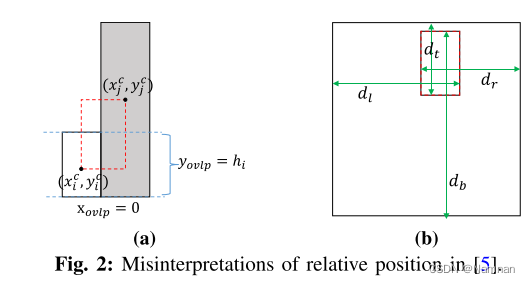
图2显示了两个模块的相对位置如何被误解的两个示例。在图2a中，$m_i$和$m_j$是分开的，因为$（x_j^c-x_i^c）$小于$（y_j^c-y_i^c）$，所以给$G_v$添加了一条边。图2b示出了两个重叠的模块$m_i$和$m_j$的示例，由于重叠区域的高度大于宽度，因此边缘被添加到$G_v$。为了克服这些缺点，我们的方法如下确定两个模块$m_i$和$m_j$的几何关系:

• 一个完全被另一个覆盖：不失一般性，我们假设$m_i$完全被$m_j$覆盖。我们选择一个方向，我们可以将$m_i$从$m_j$中移出，使得距离最小化。去除重叠后两者的相对位置决定了它们在CG中的连接方式。
• 否则：设$p_i^x，p_i^y（p_j^x，p_j^y）$为$m_i（m_j）$在X轴（Y轴）上的投影。如果它们的投影在两个轴上没有重叠，我们将遵循[5]中的规则。否则，如果Y轴（X轴）上的重叠长度较长，则将边缘添加到$G_h（G_v）$。

在使用我们的方法从DT图构建CG之后，约束图可能不足以移除所有重叠。首先，使用[10]中的方法构建表示CG中所有模块对的相对位置的两个矩阵。然后，对于CG中没有关系的任何两个模块，我们将使用前面提到的方法向相应的CG添加边。

C 两步空白删除框架

给定一个合法的布局，我们的两步空白消除框架将尝试通过重新定位和重塑空白附近的模块来提高利用率。在本节中，我们将介绍如何在我们的方法中识别目标空白，以及如何通过我们的方法减少它们。

为了识别给定布局中的空白，首先将布局分解为宽度和高度分别为$m$和$n$的$2D$网格$G$。然后对于任何网格单元$g_{ij}\in G$，我们将通过遍历每个模块及其覆盖的网格单元来标记与它重叠的模块。经过这种预处理后，我们可以通过从左下角逐行扫描网格来轻松找到矩形空白。具体地说，对于一个空的网格单元$g_{ij}$，我们将找到最大的矩形空白$w_k$，其左下角是$g_{ij}$，使得所有$g_{pq}\in w_k$都是空的。请注意，由于长而窄的通道通常会导致可路由性问题，因此我们将跳过具有大纵横比（在我们的实现中为9）的空白。

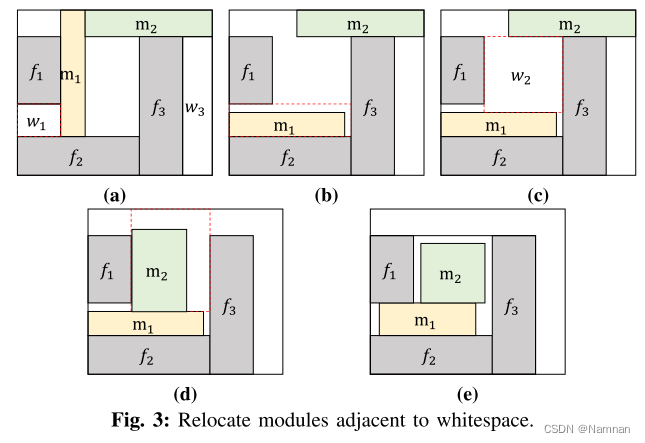
我们的空白删除框架的总体思想是将整个平面图压缩到左下角。我们的框架的第一步是消除由初始位置不佳引起的空白，而第二步则针对那些无法通过矩形模块解决的空白。这两个步骤的细节将在接下来的部分中讨论。注意，在本节的示例中，PPM被表示为$f_i$并以灰色标记，而其他PPM被假设为软模块。

1.基于位置的模块

如图1所示，在整个空白细化过程中，将使用基于约束图的合法化来确定每个模块的形状和位置。合法化的结果主要取决于模块的初始位置，这是表示为一个约束图的合法化。一些大的空白可能是由约束图误解或不良的初始位置引起的，这在生成实际的布图规划之前很难观察到。例如，如图3a所示，$f_1、m_1、m_2$之间的水平约束连同$m_2、f_3$之间的垂直约束将引起大的空白。这种空白可以很容易地通过重新定位附近的模块来解决。因此，在我们的空白消除框架的第一步，我们将通过重新定位空白附近的模块来提高利用率。

我们的基于模块重定位的方法是一个迭代过程，如算法1所示。当我们试图将模块推到轮廓的左下角时，$w_{ij}$下面的模块将被跳过，并且所选模块$M_{ij}$将按照它们与$w_{ij}$的相对位置进行处理，也就是说，我们将首先考虑$w_{ij}$顶部的模块，然后是右侧，最后是左侧。请注意，在第7行，当我们尝试将一个模块$m_{ij}$放入$w{\prime }_{ij}$时，我们会将$m_{ij}$重新整形为与$w{\prime }_{ij}$相同的长宽比，并对齐它们的左下角。如果$m_{ij}$和其他地区的重叠面积小于其面积的10%，则认为搬迁成功。图3示出了算法1的示例。首先识别空白$w_3$，但由于其纵横比太大而跳过。然后处理$w_1$，并选择模块$m_1$作为要重定位的模块。从布局中删除$m_1$后，$w_1$将扩展为一个更大的矩形，如图3b所示，其中可以成功放置$m_1$。如图3c和3d所示，$m_2$将类似地重新定位到$w_2$。最后，这些模块将通过第III-B节中提到的合法化方法进行完善。

2. 基于区域重新分配：

在重新定位空白周围的模块之后，由于矩形形状的限制，仍然有一些空白无法删除。因此，在这个阶段，一些矩形模块将被转换为直线形状，以进一步减少空白。

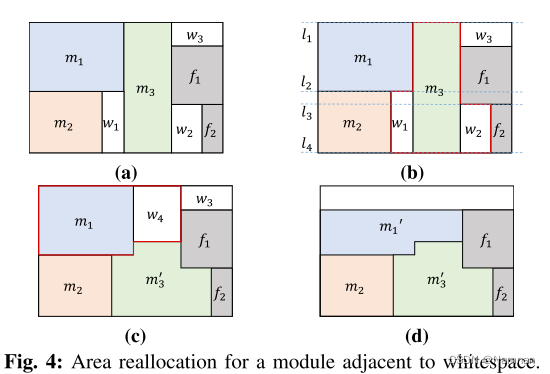
我们的基于区域重新分配的方法的细节在算法2中示出。与基于模块重定位的方法类似，重新整形和布局合法化被迭代地调用以提高利用率。当选择最佳模块来填充空白$w_i$时，我们将以与基于模块重定位的方法中提到的相同的方式考虑其相邻模块。对于白空间$w_i$的任何候选模块$m_i$，它们的公共边越长，$m_i$越优选。为了避免在模块的边界上产生“毛刺”，如果$m_i$和$w_i$之间的公共边的长度小于$m_i$的接触边的20%，则$m_i$将不会被视为填充$w_i$的候选。例如，在图4a中，当处理$w_1$时，$m_1$由于其与$w_1$的短公共边缘而被跳过。当使用$m_i$填充$W_f$和$m_i$的区域时，首先将直线区域水平地切割成矩形，如图4b所示。然后，这些矩形从底部填充$m_i$的面积，如图4c所示。

由于我们用许多规则限制非矩形模块的形状，使模块成为相对规则的形状，并且馈通[6]，引脚分配和通道布线[7]遵循布图规划以实现可布线性，因此非矩形模块对全局布线和细节布线的影响很小。

实验结果

我们的布局优化框架是用C++实现的，所有的实验都是在一个Linux服务器上进行的，该服务器具有3.00 GHz的Intel Xeon CPU（60个线程可用）。为了证明所提出的框架的有效性和可扩展性，我们使用GSRC [11]，MCNC [12]和IBM-HB+ [13]基准套件进行了一系列实验。Corblivar [1]，[14]，我们可以得到一种最先进的基于SA的布图规划器，用于生成一组法律的解决方案1，在本文的其余部分中将其称为基本布图规划。请注意，所提出的框架不假设特定的布图规划解决方案作为输入，允许其被广泛的布图规划方法采用作为后处理步骤。根据学术界通常的假设[3]，[5]，我们假设所有引脚都位于每个模块边界框的中心，IO焊盘的坐标会随着实际轮廓缩小，并将所有软模块的最大纵横比设置为3。HPWL基于每个模块的中心计算。

A 删除空白的有效性

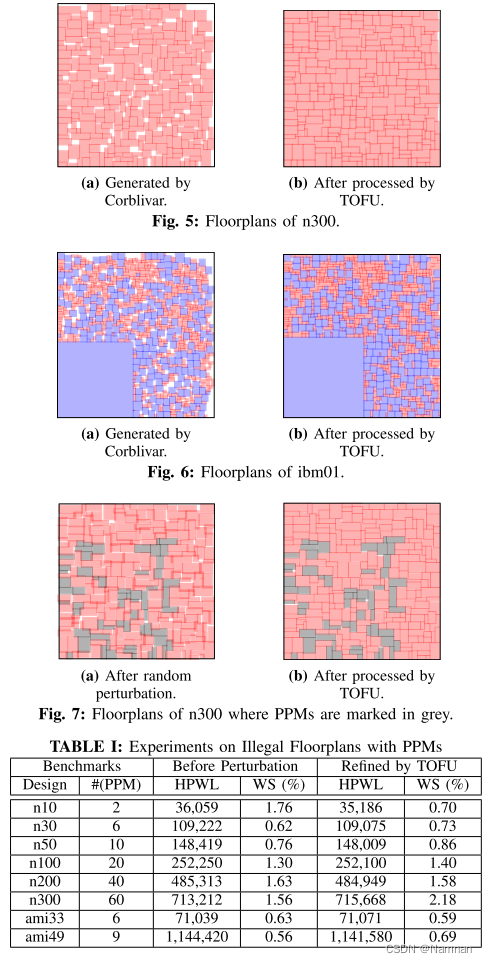
我们首先使用我们提出的框架上的基础平面图生成的Corblivar。定量结果见表II。我们可以看到我们的框架产生具有小得多的空白空间的布图规划，同时能够减少总的线长，特别是对于仅具有软模块的情况。对于像ibm01、ibm03和ibm07这样的大型情况，这是第一次实现如此低的空白级别。据我们所知，最低报告的空白比例分别为13%，14%和12%[15]。图5（图6）显示了案例n300（ibm01）优化前后的布图，其中红色和蓝色分别用于标记软模块和硬模块。可以观察到，所得到的布图规划更紧凑，导致前述的线长减少。此外，我们提出的框架在175秒内完成了最耗时的情况（ibm04），这只是Corblivar运行时间的15%。因此，我们提出的框架的可扩展性证明。

B 预放置模块的精化

然后，我们展示了TOFU的能力，处理预先放置的模块（PPM）在非法的平面图。对于这个实验，我们使用GSRC和MCNC基准。由于原始基准不包括任何PPM，我们需要自己生成它们，这将在下面讨论。为了显示我们的方法的鲁棒性，我们随机选择一些模块，使得预先放置的模块占所有模块的20%。关于PPM的一个假设是，它们通常放置在良好的位置。否则，布局利用率永远无法提高，因为轮廓是由那些放置不佳的模块决定的。在我们的实验中，我们注意到，合法化后的结果是足够好的设置PPM的位置。因此，这部分实验如下进行。
1)把Corblivar的结果合法化。
2)选择要修复的模块。
3)根据认证结果确定PPM的位置。
4)扰动可移动模块的位置。

运行我们的方法来验证其鲁棒性和有效性。表I中示出了实验结果，其表明即使使用PPM，我们也可以检索法律的布图规划。同时，仍然可以生成紧凑的布图规划，如图7b所示。

结论

在本文中，我们提出了一个两步的空白消除框架，它可以用作任何布局规划工具的后处理步骤。已经提出了几种方法来减少固定轮廓和预放置模块约束下的空白。实验结果表明，我们的方法是实用和可扩展的。未来的工作可能包括建模更多的PPA相关的约束，如路由拥塞，定时等，此外，一个算法，以产生一个接近法律的解决方案与直线形状模块建模将有助于进一步提高当前的布图规划工具链的性能。最后但并非最不重要的是，分析方法仍然需要调查，以更好地建模布图规划的具体特征，例如直线形状，可变矩形形状，最终布图规划的间隙等。