---

前言

---

一、山脉数组的峰顶索引

1.1 题目描述

描述：

符合下列属性的数组 arr 称为 山脉数组 ：

• arr.length >= 3
• 存在 i（0 < i < arr.length - 1）使得：
  • arr[0] < arr[1] < ... arr[i-1] < arr[i]
  • arr[i] > arr[i+1] > ... > arr[arr.length - 1]

给你由整数组成的山脉数组 arr ，返回满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。

你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。

---

提示：

• 3 <= arr.length <= 10^5
• 0 <= arr[i] <= 10^6
• 题目数据保证 arr 是一个山脉数组'

---

示例1：

---

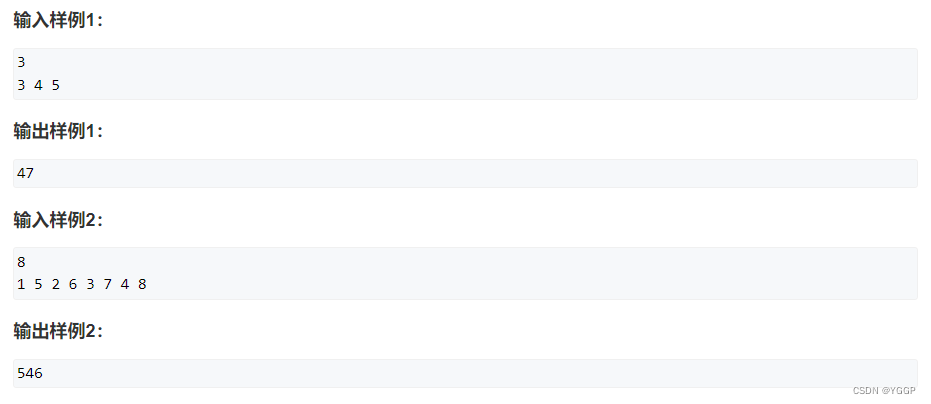
示例2：

---

示例3：

---

1.2 题目解析

1.2.1 算法原理

---

1.2.2 代码编写

---

1.2.3 题目总结

---

二、寻找峰值

2.1 题目描述

描述：

峰值元素是指其值严格大于左右相邻值的元素。

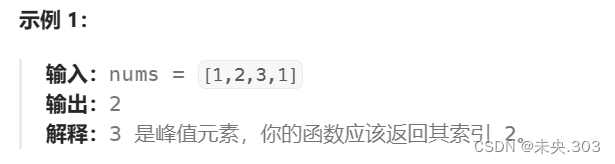
给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = - ∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

---

提示：

• 1 <= nums.length <= 1000
• -2^31 <= nums[i] <= 2^31 - 1
• 对于所有有效的 i 都有 nums[i] != nums[i + 1]

---

示例1：

---

示例2：

---

2.2 题目解析

2.2.1 算法原理

---

2.2.2 代码编写

---

2.2.3 题目总结

总结