1.希尔伯特变换的应用场景

希尔伯特变换，在数学上的含义是清晰的。它是一个数字移相器，可以把通过它的任何一个信号相移-90度。这个数学工具在信号解调时，会有非常有用的特性出现。可以看示例：

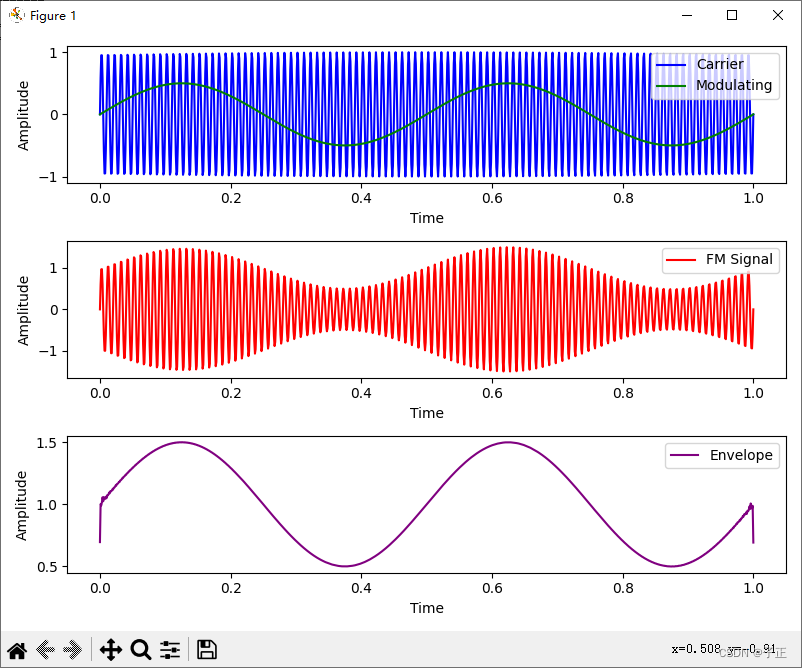
解释一下：

1.最上面的波形是载波和待叠加的低频信号。

2.中间的波形是经过信道传输的经过载波叠加的调幅波

3.是包络信号，实际上就是去除载波后的低频信号。注意，最后的载波信号被整体提升了一个幅度为载波信号幅度的直流分量。

2.相关例程

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import hilbert

# Generate a sample signal
t = np.linspace(0, 1, 1000)
frequency = 100  # Frequency of the carrier signal
amplitude = 0.5  # Amplitude of the modulating signal
carrier_signal = np.sin(2 * np.pi * frequency * t)
modulating_signal = amplitude * np.sin(2 * np.pi * 2 * t)  # Modulating signal

# Combine modulating signal and carrier signal
fm_signal = carrier_signal * (1 + modulating_signal)

# Perform Hilbert transform
analytic_signal = hilbert(fm_signal)

# Extract envelope
amplitude_envelope = np.abs(analytic_signal)

# Plotting
plt.figure(figsize=(8, 6))
plt.subplot(311)
plt.plot(t, carrier_signal, color='blue', label='Carrier')
plt.plot(t, modulating_signal, color='green', label='Modulating')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()

plt.subplot(312)
plt.plot(t, fm_signal, color='red', label='FM Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()

plt.subplot(313)
plt.plot(t, amplitude_envelope, color='purple', label='Envelope')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()

plt.tight_layout()
plt.show()

3.分析

我理解希尔伯特变换的物理含义，可以徒手编写代码完成计算。我也大致能理解它的上述应用场景。但是我很难把这两者关联起来。网络有一则看起来很能自圆其说的分享帖，关于地球物理中地震波的各个频段的震波因介质传播速度而必须进行的相位校准，那个场景无需希尔伯特变换出马。FFT本身就能搞定。FFT本身就有相位信息，用那个方法做相位修正似乎不必要。

但是，注意希尔伯特变换提供的是一个非常精准的90度移相，这意味着，控制好输入参数，它可以精准的进行特定频点的抹除。

3.1 一个物理解释 - 锁相 - 相移 - 变换 - 得到包络

希尔波特变换生成的虚部是不是实信号相移-90度的信号？

是的，希尔伯特变换生成的虚部信号通常可以看作是原始信号的相移后的信号，相移角度为-90度（或π/2 弧度）。

希尔伯特变换是一种特殊的傅里叶变换，其结果包括原始信号的实部和虚部。虚部信号经常用于表达原始信号的相位信息。而在大多数情况下，希尔伯特变换生成的虚部信号可以视为原始信号相位后退90度。

在调幅调制中，通过载波信号的幅度变化来传输调制信号的信息。希尔伯特变换可以帮助我们提取出调制信号的相位信息，从而能够进行解调。

需要注意的是，在某些特定情况下，虚部信号的相位角度可能不完全是-90度，这取决于信号的频谱特性和具体的应用场景。

它的作用是不是消除一切固定信号，只保留瞬时信号？

希尔伯特变换的一个重要应用是消除固定信号，只保留瞬时信号。瞬时信号指的是信号的瞬时特征，例如信号的瞬时幅度和瞬时相位。

希尔伯特变换通过引入90度相移来进行这种固定信号的消除。在频域中，它可以通过乘以一个复指数来实现。这个复指数在频率上具有一个极点，而在相位上具有一个-90度的延迟。

因此，希尔伯特变换可以将固定信号转换为实部为0的复数信号，而将瞬时信号保留在虚部中。通过舍弃实部为0的部分，可以消除固定信号，只留下瞬时信号。

这种特性使得希尔伯特变换在信号分析和处理中有广泛的应用，特别是在瞬时频率分析和振动信号处理等领域。

需要注意的是，希尔伯特变换并不总是能完美地消除固定信号，因为它依赖于信号的频谱特性和变换的精确度。在实际应用中，要根据具体情况来确定使用的方法和技术。

感谢您的问题，如果还有其他疑问，请随时提问。

它是怎么把固定信号滤掉的？

希尔伯特变换是一种通过引入90度相移来消除固定信号的变换方法。更具体地说，希尔伯特变换需要在频域中乘以一个复指数，这个复数在频率上具有一个极点，相位上具有一个-90度的延迟。

当信号通过希尔伯特变换时，它会被分解为实部和虚部两个部分。固定信号通常会体现在实部中，而瞬时信号则主要体现在虚部中。

由于复指数的相位延迟，固定信号在希尔伯特变换后会出现在实部，并且实部为0。同时，瞬时信号在虚部中得到保留。

因此，通过丢弃实部为0的部分，希尔伯特变换能够实现固定信号的滤除，保留瞬时信号。

需要注意的是，希尔伯特变换并不总是能够完全消除固定信号，因为它受到信号的频谱特性和变换的精确度的限制。因此，在实际应用中，要根据具体情况来确定使用的方法和技术。

他需要把载波信号对齐到0相位才行，对吧？

是的，对于希尔伯特变换的应用，如果要将所处理的信号与一个参考信号进行相位对齐，通常需要将载波信号对齐到0相位。

在某些应用中，例如调幅调制或解调中，希尔伯特变换通常用于提取信号的相位信息。而为了准确提取相位信息，需要将信号的载波信号与参考信号进行相位对齐。

相位对齐可以通过多种方式实现，具体取决于应用场景和系统要求。一种常见的方法是使用相位锁定环路（PLL）来追踪和控制相位偏移，使得载波信号与参考信号保持相位一致。另一种方法是使用触发器或延迟线等设备来调整信号的相位。

需要注意的是，在某些应用中，希尔伯特变换的结果可能对相位的初始对齐要求比较敏感。因此，在使用希尔伯特变换之前，确保载波信号与参考信号的相位对齐非常重要。

复平面的离散矢量乘法是复数域的两组矢量的逐点扭转。通过对矢量乘法之后的信号叠加上固定信号的同频信号，就可以在希尔伯特变换后，让这两个信号因为-90度的相位关系（希尔伯特变换会保证在运算过程中把这两个同频等幅信号，精确各自扭转到方向相反的位置——矢量乘法已经扭了一次，从而实现反向消除）