꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页:xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
系列专栏:xiaoxie的JAVA系列专栏——CSDN博客●'ᴗ'σσணღ*
我的目标:"团团等我💪( ◡̀_◡́ ҂)"( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝+关注(互三必回)!

一.排序的概念
二.插入排序
1.直接插入排序

1.过程
假设我们有一个数组array{15,87,63,5,98,23,1,82,10} ;我们如果使用直接插入排序的过程如下:
原始: 15 87 63 5 98 23 1 82 10
第一趟: 15 87 63 5 98 23 1 82 10
第二趟: 15 87 63 5 98 23 1 82 10
第三趟:15 63 87 5 98 23 1 82 10
......
第n(9)趟: 1 5 10 15 23 63 82 87 98
2.代码
我们可以把他写为Java代码如下:
public class Sort {
public static void insertSort(int[] array) {
insert(array,0, array.length-1);
}
private static void insert(int[] array,int start,int end) {
for (int i = start+1; i <= end; i++) {
int tmp = array[i];
int j = i-1;
for (;j >= start; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
}else {
break;
}
}
array[j+1] = tmp;
}
}
}C++版本如下
#include <iostream>
using namespace std;
class Sort {
public:
static void insertSort(int array[], int size) {
insert(array, 0, size-1);
}
private:
static void insert(int array[], int start, int end) {
for (int i = start+1; i <= end; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= start; j--) {
if (array[j] > tmp) {
array[j+1] = array[j];
} else {
break;
}
}
array[j+1] = tmp;
}
}
};3.时间复杂度
最好情况下:
直接插入排序在最好情况下也就是在数据都有序的情况下为O(n)。
最坏情况下:
直接插入排序的最坏情况也就是在数据为逆序的情况下为O(n^2)。
4.空间复杂度
因为直接插入排序是在本数组中实现的没有借用辅助空间所以为O(1)。
5.稳定性
该算法为稳定的
值得注意的是元素集合越接近有序,直接插入排序算法的时间效率越高。
2. 希尔排序( 缩小增量排序 )
1.过程
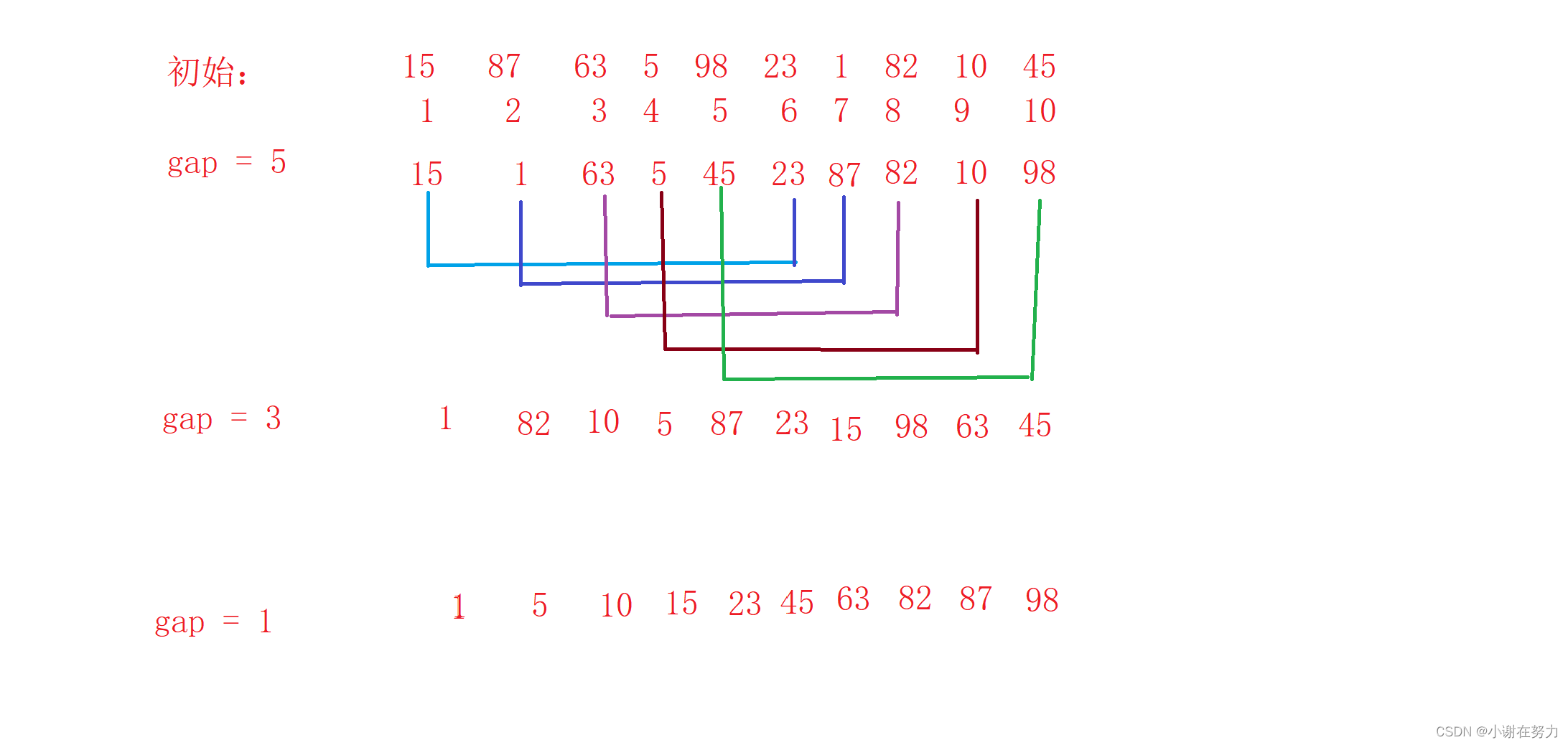
2.代码
java
public class Sort {
public static void shellSort(int[] array) {
int gap = array.length;
while (gap > 1) {
gap /= 2;
Shell(array,gap);
}
}
private static void Shell(int[] array,int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i-gap;
for (; j >= 0; j-=gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = tmp;
}
}
}
C++
#include <iostream>
using namespace std;
void shellSort(int array[], int size) {
int gap = size;
while (gap > 1) {
gap /= 2;
Shell(array, size, gap);
}
}
void Shell(int array[], int size, int gap) {
for (int i = gap; i < size; i++) {
int tmp = array[i];
int j = i - gap;
for (; j >= 0; j -= gap) {
if (array[j] > tmp) {
array[j + gap] = array[j];
} else {
break;
}
}
array[j + gap] = tmp;
}
}3.时间复杂度

《数据结构-用面向对象方法与C++描述》--- 殷人昆

4.空间复杂度
因为希尔排序是直接插入排序的优化所以是在本数组中实现的没有借用辅助空间所以为O(1)。
5.稳定性
不稳定
6.希尔排序的特性
三.选择排序
3.直接选择排序
1.过程
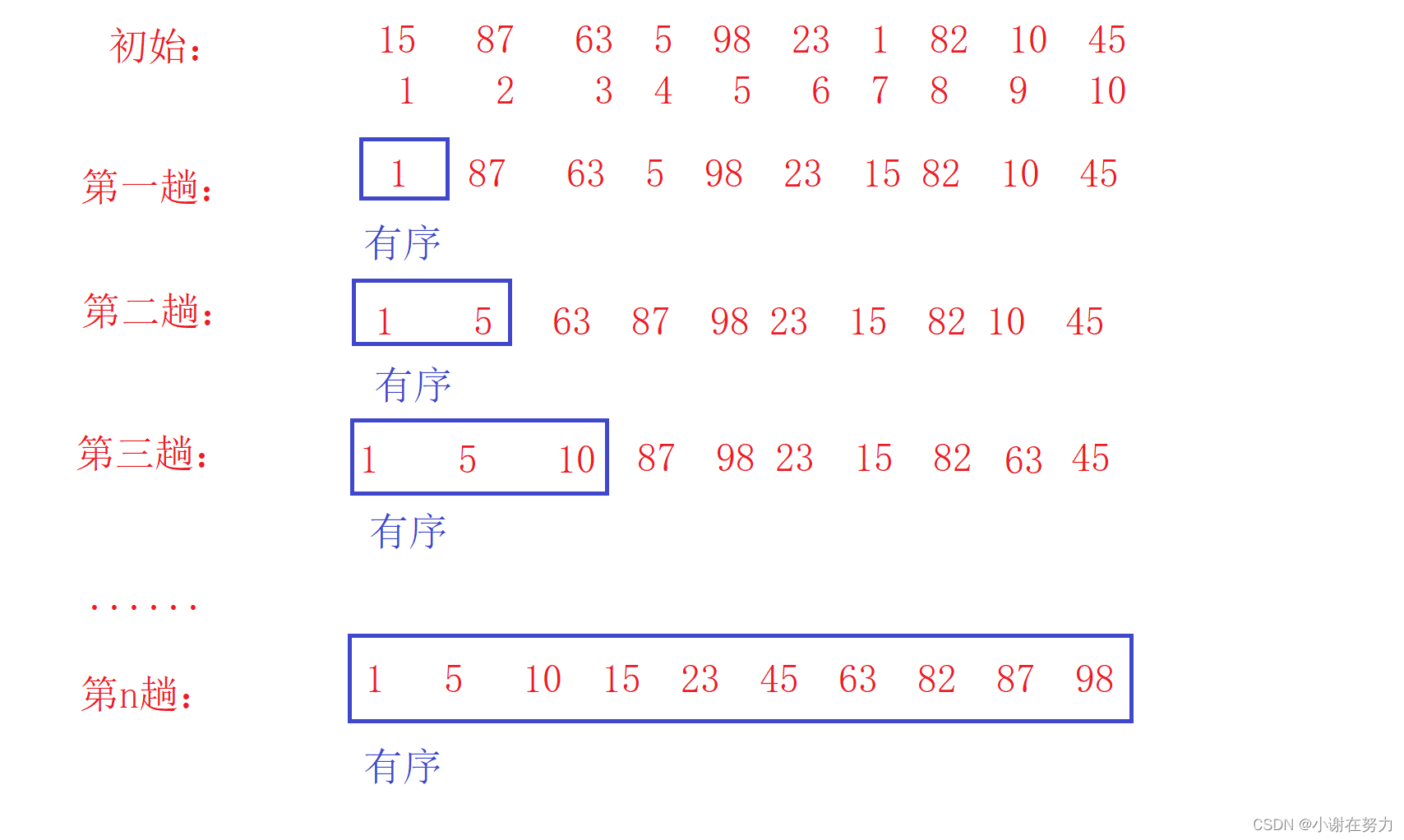
2.代码
Java
public class Sort {
public static void selectSort(int[] array) {
select(array,0, array.length-1);
}
private static void select(int[] array,int start,int end) {
for (int i = 0; i <= end ; i++) {
int minIndex = i;
for (int j = i+1; j <= end ; j++) {
if(array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array,i,minIndex);
}
}
private static void swap(int[]array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}#include <iostream>
using namespace std;
void selectSort(int array[], int size) {
select(array, 0, size - 1);
}
void select(int array[], int start, int end) {
for (int i = 0; i <= end; i++) {
int minIndex = i;
for (int j = i + 1; j <= end; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array, i, minIndex);
}
}
void swap(int array[], int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
3.时间复杂度
最好情况和最坏情况都为:O(n^2) 所以不是很推荐使用
4.空间复杂度
因为直接选择排序是在本数组中实现的没有借用辅助空间所以为O(1)。
5.稳定性
不稳定
4.堆排序(需要重点掌握)
1.过程
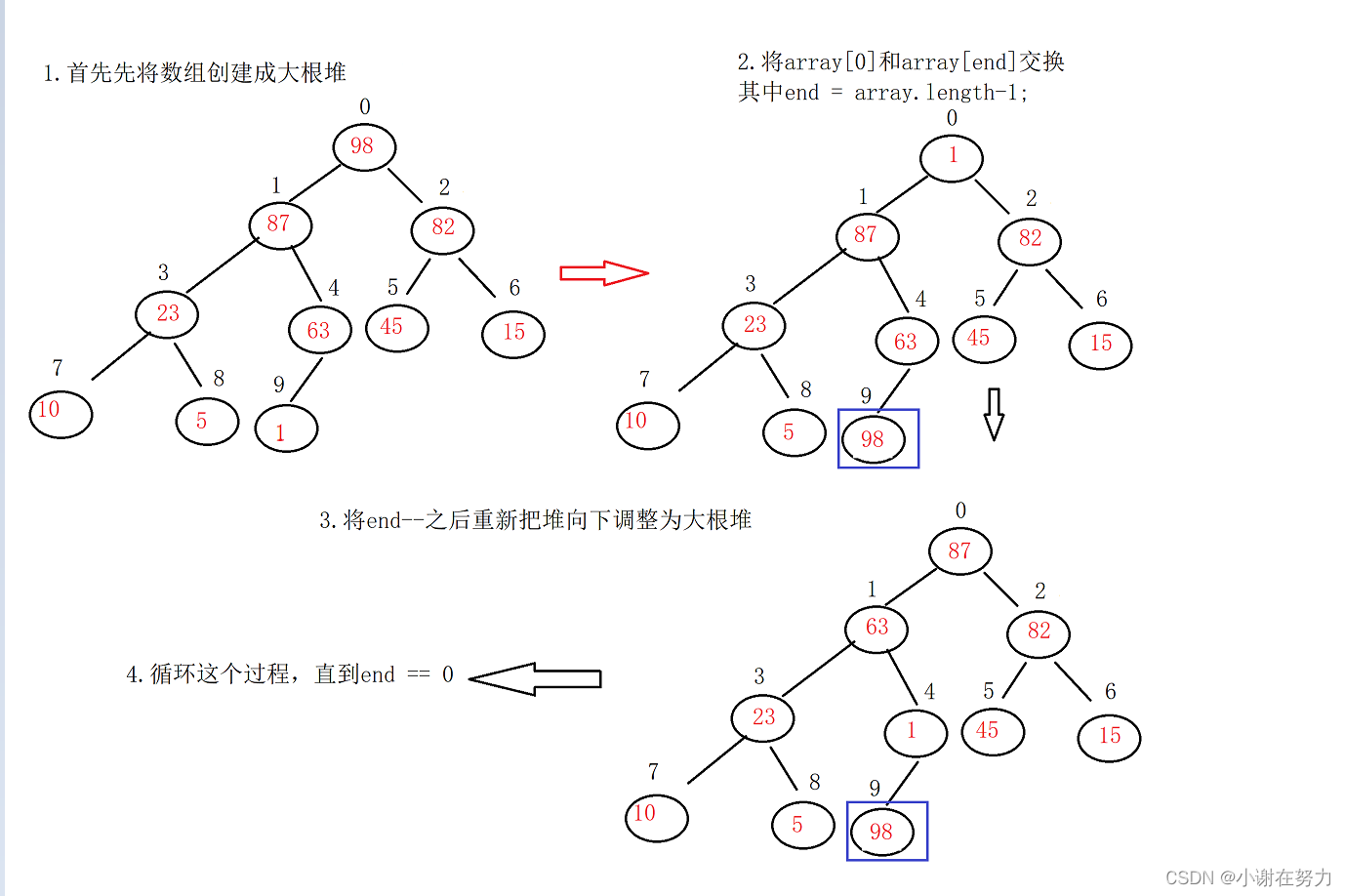
2.代码
Java
private static void swap(int[]array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void heapSort(int[] array) {
crateHeap(array);//首先创建大根堆
int end = array.length-1;
while (end >= 0) {
swap(array,0,end);
siftDown(array,0,end);
end--;
}
}
// 创建大根堆
private static void crateHeap(int[] array) {
for (int parent = (array.length-1-1)/2; parent >= 0; parent--) {
siftDown(array,parent,array.length);
}
}
// 向下调整
private static void siftDown(int[] array,int parent,int len) {
int child = 2*parent+1;
while (child < len) {
if(child+1 < len && array[child] < array[child+1]) {
child++;
}
if(array[child] > array[parent]) {
swap(array,child,parent);
parent = child;
child = 2*parent+1;
}else {
break;
}
}
}C++
#include <iostream>
using namespace std;
void swap(int array[], int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
void heapSort(int array[], int length) {
createHeap(array, length); // 首先创建大根堆
int end = length - 1;
while (end >= 0) {
swap(array, 0, end);
siftDown(array, 0, end);
end--;
}
}
// 创建大根堆
void createHeap(int array[], int length) {
for (int parent = (length - 2) / 2; parent >= 0; parent--) {
siftDown(array, parent, length);
}
}
// 向下调整
void siftDown(int array[], int parent, int len) {
int child = 2 * parent + 1;
while (child < len) {
if (child + 1 < len && array[child] < array[child + 1]) {
child++;
}
if (array[child] > array[parent]) {
swap(array, child, parent);
parent = child;
child = 2 * parent + 1;
} else {
break;
}
}
}
3.时间复杂度
因为堆是一颗完全二叉树所以他的时间复杂度为:O(n*logN)。
4.空间复杂度
没有借助辅助空间所以空间复杂度为:O(1)。
5.稳定性
不稳定
四.交换排序
5.冒泡排序
1.过程
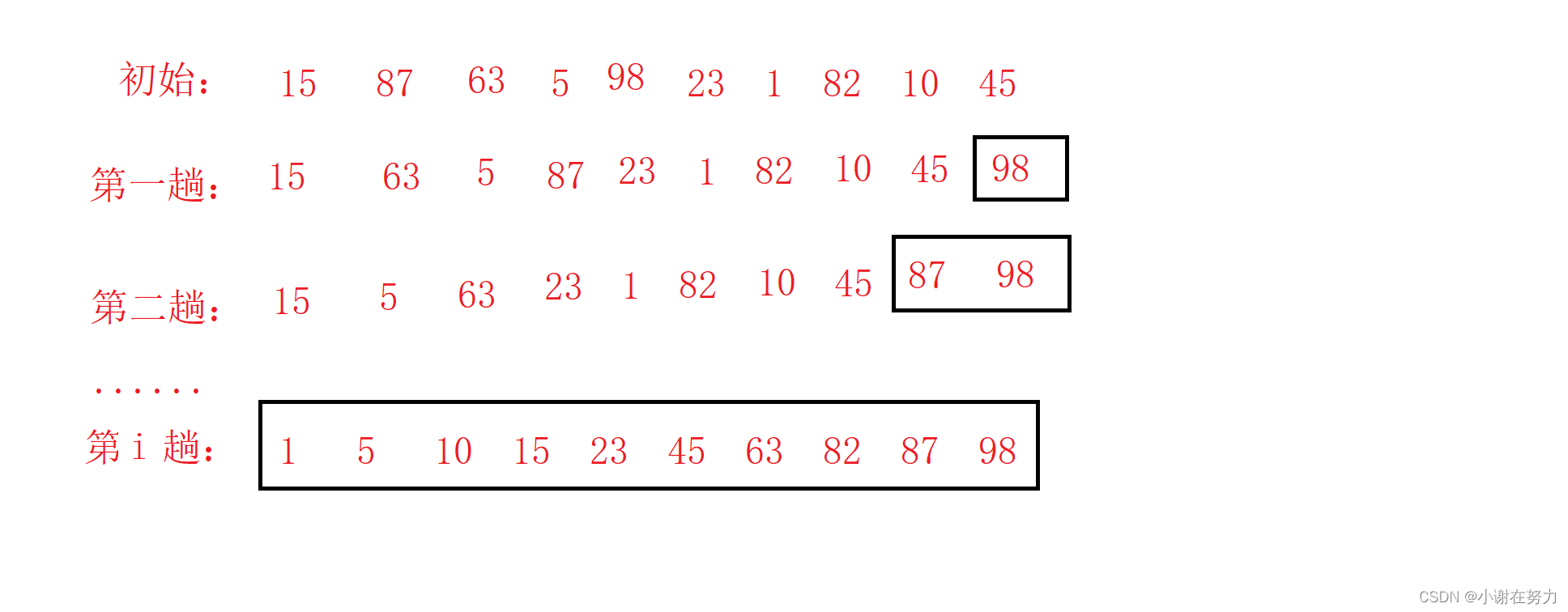
2.代码
Java
private static void swap(int[]array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void bubbleSort(int[] array) {
//10个元素遍历9趟
for (int i = 0; i < array.length-1; i++) {
boolean flag = false;
for (int j = 0; j < array.length-1-i; j++) {
if(array[j] > array[j+1]) {
swap(array,j,j+1);
flag = true;
}
}
//没有交换就证明有序
if(flag == false) {
return;
}
}
}C++
#include <iostream>
using namespace std;
void swap(int array[], int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
void bubbleSort(int array[], int length) {
// 对于10个元素,遍历9趟
for (int i = 0; i < length - 1; i++) {
bool flag = false;
for (int j = 0; j < length - 1 - i; j++) {
if (array[j] > array[j + 1]) {
swap(array, j, j + 1);
flag = true;
}
}
// 若没有交换发生,则证明数组已有序
if (!flag) {
return;
}
}
}3.时间复杂度
最好情况下:
冒泡排序在最好情况下也就是在数据都有序的情况下为O(n)。
最坏情况下:
冒泡排序的最坏情况也就是在数据为逆序的情况下为O(n^2)。
4.空间复杂度
没有借助辅助空间所以空间复杂度为:O(1)。
5.稳定性
稳定
6.快速排序(重点掌握)
1.1Hoare法过程
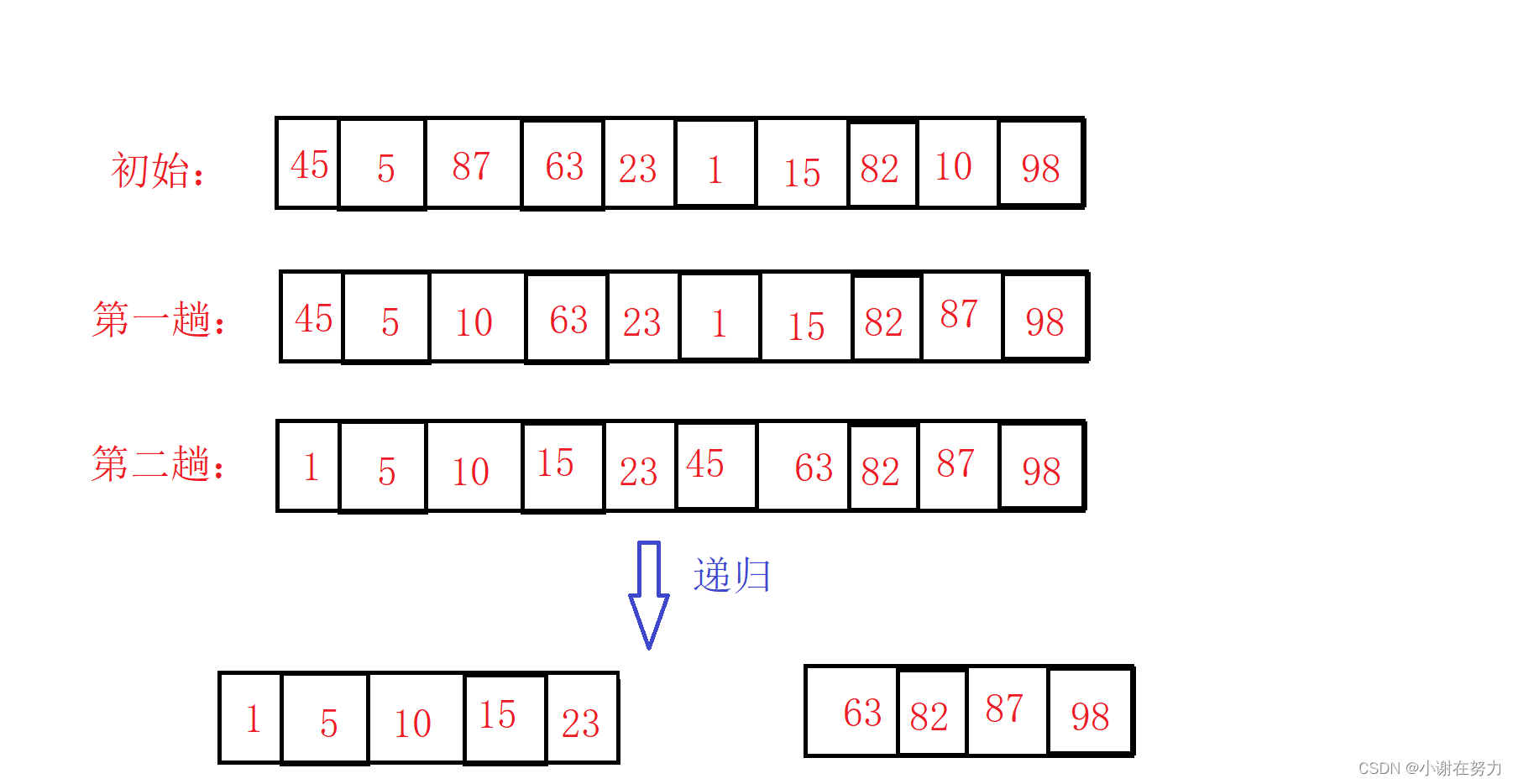
1.2Hoare法代码
private static void swap(int[]array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void quickSort(int[] array) {
quick(array,0, array.length-1);
}
private static void quick(int[] array,int left,int right) {
if(right-left <= 1) {
return;
}
//三数取中法
int index = middleNum(array,left,right);
swap(array,left,index);
int pivot = partitionHoare(array,left,right);
quick(array,left,pivot-1);//递归左边
quick(array,pivot+1,right);//递归右边
}
//三数取中
private static int middleNum(int[] array,int start,int end) {
int mid = start+((end-start)>>1);
if(array[start] < array[end]) {
if(array[mid] > array[end]) {
return end;
} else if (array[mid] < array[start]) {
return start;
}else {
return mid;
}
}else {
if(array[mid] < array[end]) {
return end;
} else if (array[mid] > array[start]) {
return start;
}else {
return mid;
}
}
}
//获取基准值的位置使用Hoare法
private static int partitionHoare(int[] array,int left ,int right) {
int tmp = array[left];//基准值
int i = left;//记录下来基准值开始的下标
while (left < right) {
while (left < right && array[right] >= tmp) {
right--;
}
while (left < right && array[left] <= tmp) {
left++;
}
swap(array,left,right);
}
swap(array,left,i);
return left;
}C++版本
#include <iostream>
using namespace std;
void swap(int array[], int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
void quickSort(int array[], int length) {
quick(array, 0, length - 1);
}
void quick(int array[], int left, int right) {
if (right - left <= 1) {
return;
}
// 三数取中法
int index = middleNum(array, left, right);
swap(array, left, index);
int pivot = partitionHoare(array, left, right);
quick(array, left, pivot - 1); // 递归左边
quick(array, pivot + 1, right); // 递归右边
}
// 三数取中
int middleNum(int array[], int start, int end) {
int mid = start + ((end - start) >> 1);
if (array[start] < array[end]) {
if (array[mid] > array[end]) {
return end;
} else if (array[mid] < array[start]) {
return start;
} else {
return mid;
}
} else {
if (array[mid] < array[end]) {
return end;
} else if (array[mid] > array[start]) {
return start;
} else {
return mid;
}
}
}
// 获取基准值的位置使用Hoare法
int partitionHoare(int array[], int left, int right) {
int tmp = array[left]; // 基准值
int i = left; // 记录下来基准值开始的下标
while (left < right) {
while (left < right && array[right] >= tmp) {
right--;
}
while (left < right && array[left] <= tmp) {
left++;
}
swap(array, left, right);
}
swap(array, left, i);
return left;
}2.1挖坑法过程(重点掌握)考试选择题过程一般使用挖坑法

2.2 挖坑法代码(重点掌握)
Java
private static void swap(int[]array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void quickSort(int[] array) {
quick(array,0, array.length-1);
}
private static void quick(int[] array,int left,int right) {
if(right-left <= 1) {
return;
}
//三数取中法
int index = middleNum(array,left,right);
swap(array,left,index);
int pivot = partition(array,left,right);
quick(array,left,pivot-1);//递归左边
quick(array,pivot+1,right);//递归右边
}
//三数取中
private static int middleNum(int[] array,int start,int end) {
int mid = start+((end-start)>>1);
if(array[start] < array[end]) {
if(array[mid] > array[end]) {
return end;
} else if (array[mid] < array[start]) {
return start;
}else {
return mid;
}
}else {
if(array[mid] < array[end]) {
return end;
} else if (array[mid] > array[start]) {
return start;
}else {
return mid;
}
}
}
//获取基准值的位置使用挖坑法
private static int partition(int[] array,int left ,int right) {
int tmp = array[left];//记录基准值
while (left < right) {
while (left < right && array[right] >= tmp) {
right--;
}
array[left] = array[right];
while (left < right && array[left] <= tmp) {
left++;
}
array[right] = array[left];
}
array[left] = tmp;// 将基准值放入正确位置
return left;
}C++
#include <iostream>
using namespace std;
void swap(int array[], int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
void quickSort(int array[], int length) {
quick(array, 0, length - 1);
}
void quick(int array[], int left, int right) {
if (right - left <= 1) {
return;
}
// 三数取中法
int index = middleNum(array, left, right);
swap(array, left, index);
int pivot = partition(array, left, right);
quick(array, left, pivot - 1); // 递归左边
quick(array, pivot + 1, right); // 递归右边
}
// 三数取中
int middleNum(int array[], int start, int end) {
int mid = start + ((end - start) >> 1);
if (array[start] < array[end]) {
if (array[mid] > array[end]) {
return end;
} else if (array[mid] < array[start]) {
return start;
} else {
return mid;
}
} else {
if (array[mid] < array[end]) {
return end;
} else if (array[mid] > array[start]) {
return start;
} else {
return mid;
}
}
}
// 获取基准值的位置使用挖坑法
int partition(int array[], int left, int right) {
int pivot = array[left]; // 基准值
while (left < right) {
while (left < right && array[right] >= pivot) {
right--;
}
array[left] = array[right];
while (left < right && array[left] <= pivot) {
left++;
}
array[right] = array[left];
}
array[left] = pivot; // 将基准值放入正确位置
return left;
}
3.时间复杂度
最好情况下数据为无序的时候为O(n*logN)。
最坏情况下数据为有序或者是逆序的时候为O(n^2)。
4.空间复杂度
在递归调用过程中,需要使用O(log n)的栈空间来存储递归调用的上下文信息所以空间复杂度为:O(logN)。
5.稳定性
不稳定
7.归并排序(重点掌握)
1.过程
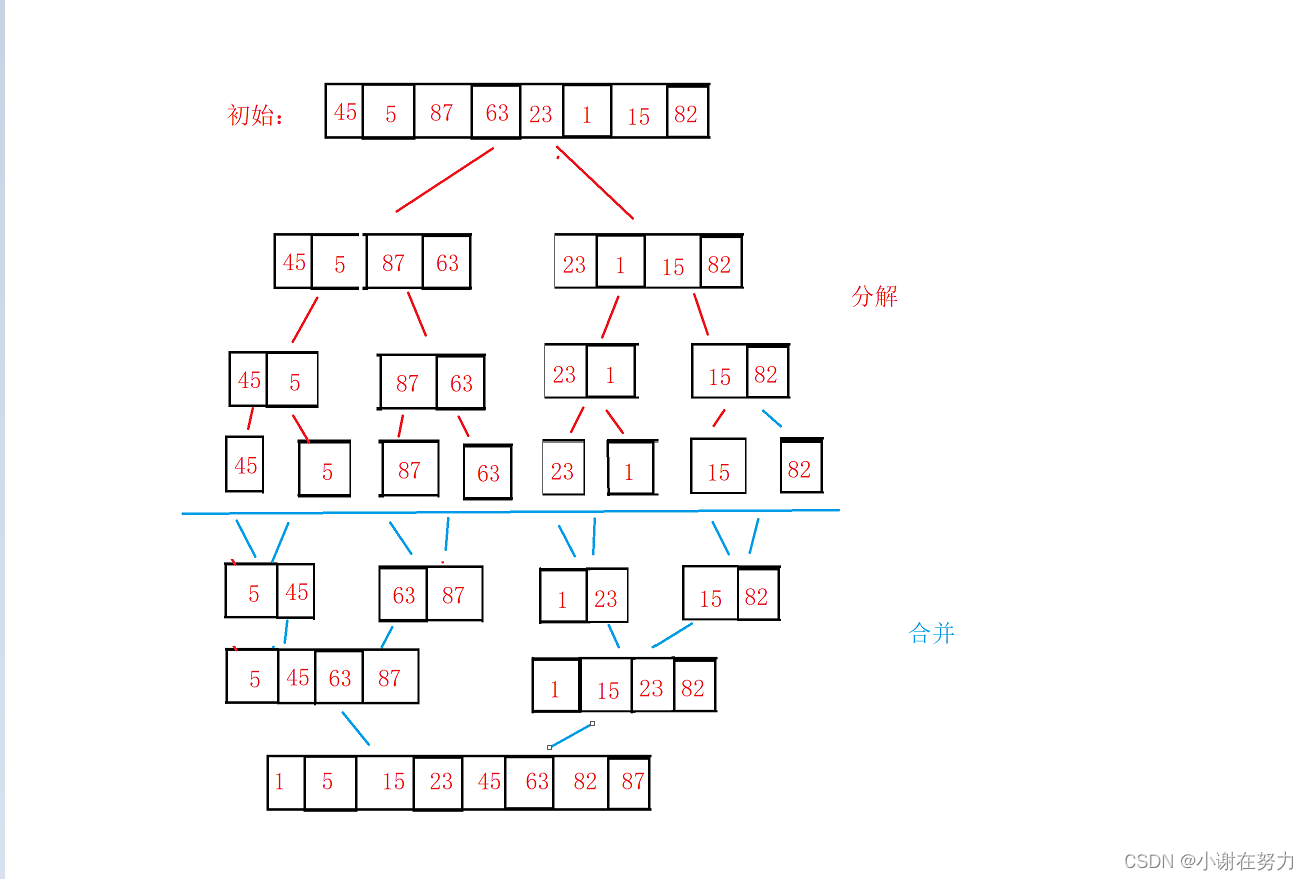
2.代码
Java
public static void mergeSort(int[] array) {
mergeFunc(array,0,array.length-1);
}
private static void mergeFunc(int[] array,int left,int right) {
if(left >= right) {
return;
}
int mid = left + ((right-left) >> 1);
//开始分解
mergeFunc(array,left,mid);
mergeFunc(array, mid+1, right);
//开始合并
merge(array,left,right,mid);
}
private static void merge(int[] array,int left,int right,int mid) {
int s1 = left;
int e1 = mid;
int s2 = mid+1;
int e2 = right;
int[] tmp = new int[right-left+1];//创建一个临时数组来储存数据
int k = 0;//临时数组下标
while (s1 <= e1 && s2 <= e2) {
if(array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
}else {
tmp[k++] = array[s2++];
}
}
//看那个数组还有数据就拷贝过去
while (s1 <= e1) {
tmp[k++] = array[s1++];
}
while (s2 <= e2) {
tmp[k++] = array[s2++];
}
//3.拷贝到源数组
for (int i = 0; i < k; i++) {
array[i+left] = tmp[i];
}
}C++
#include <iostream>
using namespace std;
void mergeSort(int array[], int length) {
mergeFunc(array, 0, length - 1);
}
void mergeFunc(int array[], int left, int right) {
if (left >= right) {
return;
}
int mid = left + ((right - left) >> 1);
// 开始分解
mergeFunc(array, left, mid);
mergeFunc(array, mid + 1, right);
// 开始合并
merge(array, left, right, mid);
}
void merge(int array[], int left, int right, int mid) {
int s1 = left;
int e1 = mid;
int s2 = mid + 1;
int e2 = right;
int tmp[right - left + 1]; // 创建一个临时数组来储存数据
int k = 0; // 临时数组下标
while (s1 <= e1 && s2 <= e2) {
if (array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
} else {
tmp[k++] = array[s2++];
}
}
// 看那个数组还有数据就拷贝过去
while (s1 <= e1) {
tmp[k++] = array[s1++];
}
while (s2 <= e2) {
tmp[k++] = array[s2++];
}
// 3.拷贝到源数组
for (int i = 0; i < k; i++) {
array[i + left] = tmp[i];
}
}3.时间复杂度
时间复杂度为O(n*logN)。
4.空间复杂度
因为需要借助临时数组所以空间复杂度为O(n)。
5.稳定性
稳定
五.各个排序算法的时间复杂度和空间复杂度以及稳定性总结

以上就是关于基于比较排序的所以的内容了,如果有帮助到你,创作不易希望可以给博主一个关注,感谢你的阅读,希望能够对你有所帮助












![uniapp对接微信APP支付返回requestPayment:fail [payment微信:-1]General errors错误-全网总结详解](https://img-blog.csdnimg.cn/742bc7da3e274776bc2280299e3701aa.png)