---

题目链接

链接: P1433 吃奶酪

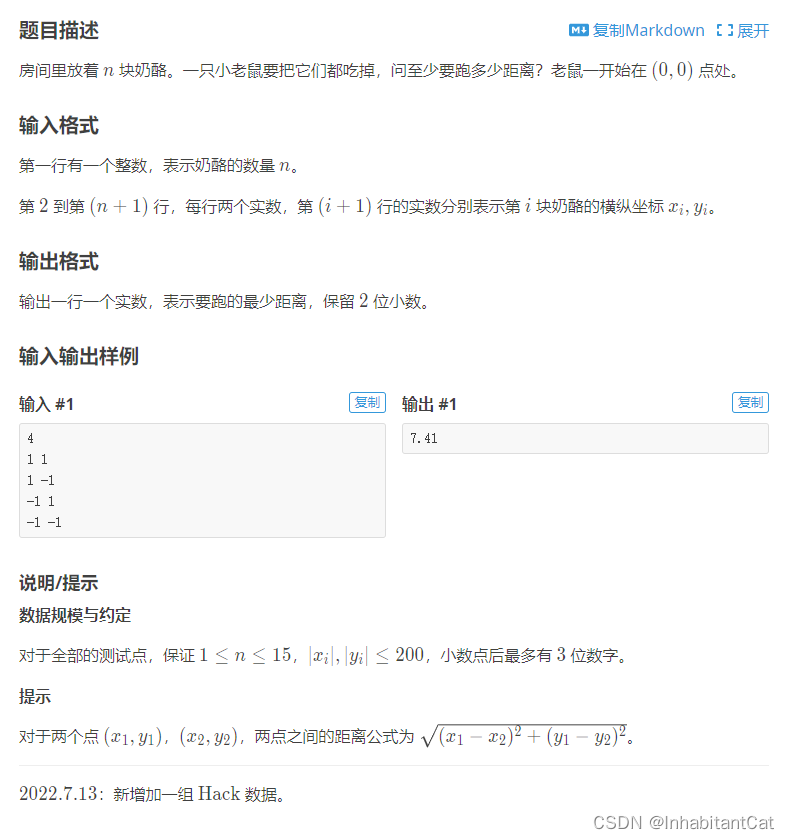
题目描述

解题思路

首先，这个程序是用来解决洛谷上题目编号为 P1433 的问题——吃奶酪，使用了状压DP算法。

整体算法的思路是利用动态规划，通过状态压缩来解决问题。题目要求找出一条路径，使得从原点出发，经过所有的奶酪点且最后返回原点，使得总路径最短。程序中的主要数据结构是数组和存储奶酪坐标的变量。

具体来说，主要分为以下步骤：

1. 预处理阶段：

   • 预先计算出每两个奶酪点之间的距离，存储在数组 a 中，用于后续的状态转移计算。

2. 初始化阶段：

   • 初始化状态压缩DP数组 F，将其所有值置为无穷大。

3. 状态转移阶段：

   • 通过状态压缩和动态规划的思想，枚举所有可能的路径状态（使用二进制表示），并根据状态转移方程更新数组 F 中每一种状态的最短距离。

4. 输出结果：

   • 最后输出结果，找到包含所有奶酪点的最短路径的长度。

代码实现

#include <cstdio>
#include <cstring> 
#include <cmath> 
#define min(a,b) (((a)<(b))?(a):(b)) 
//洛谷 P1433 吃奶酪 状压DP
double a[20][20];//预处理，从第i块到第j块的距离，使用两点之间距离公式 
double x[20],y[20];//每块奶酪的横、纵坐标
double F[18][34000];//状压DP数组 在第i个点上，走过的二进制状态的十进制表达为j时，最短的距离 
int N; 
double distance(int v,int w)//计算第v个和第w个奶酪之间的距离 
{
	return sqrt((x[v]-x[w])*(x[v]-x[w])+(y[v]-y[w])*(y[v]-y[w]));//两点间距离公式 
}
int main()
{
	int i,j,k;
	double ans;
	memset(F,127,sizeof(F));//这样可以给浮点数赋值无穷大 
	ans=F[0][0];
	scanf("%d",&N);
	for(i=1;i<=N;i++)
	{
		scanf("%lf%lf",&x[i],&y[i]);//数据读入 
	}
	x[0]=0;y[0]=0;
	for(i=0;i<=N;i++)
	{
		for(j=i+1;j<=N;j++)
		{
			a[i][j]=distance(i,j);//初始化距离数组 
			a[j][i]=a[i][j];
		}
	} 
	for(i=1;i<=N;i++)//初始化 
	{
		F[i][(1<<(i-1))]=a[0][i];//在i点上且只有经过i点时距离是原点到i点的距离 
	}
	for(k=1;k<(1<<N);k++)//枚举所有二进制的状态 
	{
		for(i=1;i<=N;i++)
		{
			if((k&(1<<(i-1)))==0)
				continue;//i的位置没被走过，所以不需要再继续计算了 
			for(j=1;j<=N;j++)
			{
				if(i==j)
					continue;//同一个点不需要再计算 
				if((k&(1<<(j-1)))==0)
					continue;//j的位置没走过  
				F[i][k]=min(F[i][k],F[j][k-(1<<(i-1))]+a[i][j]);
			} 
		} 
	} 
	for(i=1;i<=N;i++)
	{
		ans=min(ans,F[i][(1<<N)-1]);
	}
	printf("%.2f\n",ans);
}

总结

状态压缩DP算法