一、实验目的
了解鲁滨逊归结算法原理,利用Python编写程序,实现鲁滨逊归结算法。
二、实验原理
鲁滨逊归结原理又称为消解原理,是鲁滨逊提出的一种证明子句集不可满足性,从而实现定理证明的一种理论及方法。它是机器定理证明的基础。
由谓词公式转化为子句集的过程可以看出,在子句集中子句之间是合取关系,其中只要有一个子句不可满足,则子句集就不可满足。由于空子句是不可满足的,所以,若一个子句集中包含空子句,则这个子句集一定是不可满足的。鲁宾逊归结原理就是基于这个思想提出来的。其基本方法是:检查子句集S中是否包含空子句,若包含,则S不可满足;若不包含,就在子句集中选择合适的子句进行归结,一旦通过归结得到空子句,就说明子句集S是不可满足的。
三、实验过程记录
以下为归结原理中归结过程的树形表示:

以下列题目为例,对归结原理进行应用。

下面我们用Python实现命题逻辑归结原理的演绎推理:
S = [] # 以列表形式存储子句集S
def readClauseSet(filePath):
global S
for line in open(filePath, mode = 'r', encoding = 'utf-8'):
line = line.replace(' ', '').strip()
line = line.split('∨')
S.append(line)
#取反
def opposite(clause):
if '~' in clause:
return clause.replace('~', '')
else:
return '~' + clause
#归结
def resolution():
global S
end = False
while True:
if end: break
father = S.pop()
for i in father[:]:
if end: break
for mother in S[:]:
if end: break
j = list(filter(lambda x: x == opposite(i), mother))
if j == []:
continue
else:
print('\n亲本子句:' + ' ∨ '.join(father) + ' 和 ' + ' ∨ '.join(mother))
father.remove(i)
mother.remove(j[0])
if(father == [] and mother == []):
print('归结式:NIL')
end = True
elif father == []:
print('归结式:' + ' ∨ '.join(mother))
elif mother == []:
print('归结式:' + ' ∨ '.join(mother))
else:
print('归结式:' + ' ∨ '.join(father) + ' ∨ ' + ' ∨ '.join(mother))
def main():
filePath = r'./S.txt'
readClauseSet(filePath)
print('--------命题逻辑归结推理--------')
resolution()
if __name__ == '__main__':
main()四、实验结果
选取以下题目进行测试:已知命题公式集S,求证R
![]()
首先需要手动将谓词公式化为子句集,并存储到S.txt文件中。过程如下:
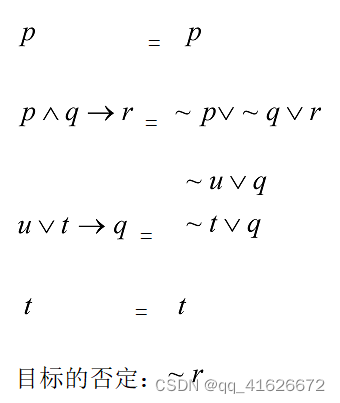
在S.txt中存储的内容作为后续归结的子句集。

运行程序,得到如下归结过程。

五、实验过程中存在的问题及解决方案
该实验的理论部分以及手动进行归结过程并不复杂,只需要认真仔细即可完成。但利用Python进行归结的时候出现了不小的困难。通过上网查询资料和参考别人的代码,最后实现了对命题子句集进行归结的代码,后续还需要继续努力。
六、实验总结
本次实验利用手动归结和Python编程分别对鲁宾逊归结原理进行了学习。归结原理在命题逻辑和谓词逻辑中的定义如下:
(1)命题逻辑中的归结原理
设C1与C2是子句集中的任意两个子句,如果C1中的文字L1与C2中的文字L2互补,那么从C1和C2中分别消去L1和L2,并将两个子句中余下的部分析取,构成一个新语句C12,这一过程称为归结。C12称为C1和C2的归结式,C1和C2称为C12的亲本子句。
(2)谓词逻辑中的归结原理
子句C1与C2的归结式是下列二元归结式之一:
a)C1与C2的二元归结式
b)C1的因子C1σ1与C2的二元归结式
c)C1与C2的因子C2σ2的二元归结式

![[docker] Docker镜像的创建以及Dockerfile的使用](https://img-blog.csdnimg.cn/direct/dd7fcea794b5400fb642a2abb69101b6.png)