前提
这篇博客是对最近一个有关无人机拍摄图像项目中所学到的新知识的一个总结,比较杂乱,没有固定的写作顺序。
无人机坐标系旋转问题
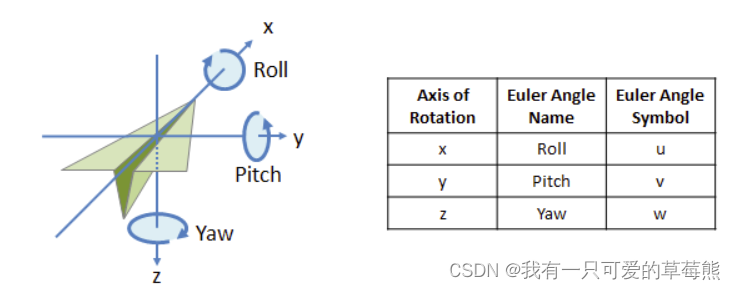
上图是无人机坐标系,绕x轴是翻滚(Roll),绕y轴是俯仰(Pitch),绕z轴是偏航(Yaw)。在初始位置,无人机坐标系和世界坐标系是对齐的,在坐标系中存在一个原始点
(
x
0
,
y
0
,
z
0
)
(x_0,y_0,z_0)
(x0,y0,z0),那么当无人机翻滚、俯仰、偏航后,此时的原始点被转动到了哪个位置处?
首先是绕x轴的翻滚,翻滚角为u,旋转矩阵为:
R
x
(
u
)
=
[
1
0
0
0
c
o
s
(
u
)
−
s
i
n
(
u
)
0
s
i
n
(
u
)
c
o
s
(
u
)
]
R_x(u)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(u) & -sin(u) \\ 0 & sin(u) & cos(u) \end{bmatrix}
Rx(u)=
1000cos(u)sin(u)0−sin(u)cos(u)
可以看到,这个旋转矩阵和三维空间中某一点绕x轴旋转的旋转矩阵一样。
旋转后的坐标则为:
[
x
1
y
1
z
1
]
=
R
x
(
u
)
[
x
0
y
0
z
0
]
\begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix}= R_x(u)\begin{bmatrix} x_0 \\ y_0 \\ z_0 \end{bmatrix}
x1y1z1
=Rx(u)
x0y0z0
接下来是绕y轴的俯仰,俯仰角为v,旋转矩阵为:
R
y
(
v
)
=
[
c
o
s
(
v
)
0
s
i
n
(
v
)
0
1
0
−
s
i
n
(
v
)
0
c
o
s
(
v
)
]
R_y(v)=\begin{bmatrix} cos(v) & 0 & sin(v) \\ 0 & 1 & 0 \\ -sin(v) & 0 & cos(v) \end{bmatrix}
Ry(v)=
cos(v)0−sin(v)010sin(v)0cos(v)
可以看到,这个旋转矩阵和三维空间中某一点绕y轴旋转的旋转矩阵一样。
旋转后的坐标则为:
[
x
2
y
2
z
2
]
=
R
y
(
u
)
[
x
1
y
1
z
1
]
\begin{bmatrix} x_2 \\ y_2 \\ z_2 \end{bmatrix}= R_y(u)\begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix}
x2y2z2
=Ry(u)
x1y1z1
接下来是绕z轴的偏航,偏航角为w,旋转矩阵为:
R
z
(
v
)
=
[
c
o
s
(
w
)
−
s
i
n
(
w
)
0
s
i
n
(
w
)
c
o
s
(
w
)
0
0
0
1
]
R_z(v)=\begin{bmatrix} cos(w) & -sin(w) & 0 \\ sin(w) & cos(w) & 0 \\ 0 & 0 & 1 \end{bmatrix}
Rz(v)=
cos(w)sin(w)0−sin(w)cos(w)0001
可以看到,这个旋转矩阵和三维空间中某一点绕z轴旋转的旋转矩阵一样。
旋转后的坐标则为:
[
x
3
y
3
z
3
]
=
R
z
(
u
)
[
x
2
y
2
z
2
]
\begin{bmatrix} x_3 \\ y_3 \\ z_3 \end{bmatrix}= R_z(u)\begin{bmatrix} x_2 \\ y_2 \\ z_2 \end{bmatrix}
x3y3z3
=Rz(u)
x2y2z2
将三个旋转矩阵结合起来就就是:
[
x
3
y
3
z
3
]
=
R
z
(
w
)
×
R
y
(
v
)
×
R
x
(
u
)
[
x
0
y
0
z
0
]
\begin{bmatrix} x_3 \\ y_3 \\ z_3 \end{bmatrix}= R_z(w)\times R_y(v)\times R_x(u)\begin{bmatrix} x_0 \\ y_0 \\ z_0 \end{bmatrix}
x3y3z3
=Rz(w)×Ry(v)×Rx(u)
x0y0z0
可以看到这里面有很重要的一点就是:
R
z
(
w
)
、
R
y
(
v
)
、
R
x
(
u
)
R_z(w)、R_y(v)、R_x(u)
Rz(w)、Ry(v)、Rx(u)相乘时的顺序不能发生改变,一旦发生改变(矩阵相乘没有交换律),则结果也会发生变化。
对上面进行总结,整体上如下图所示:

已知在无人机坐标系下的一点
(
x
0
,
y
0
,
z
0
)
(x_0,y_0,z_0)
(x0,y0,z0),求无人机在翻滚u度,俯仰v度,偏航w度后的点坐标
(
x
3
,
y
3
,
z
3
)
(x_3,y_3,z_3)
(x3,y3,z3)。计算公式如上所示。
图像相关问题
视场角
一般来说,相机的视场角(FOV)有三个,H FOV(水平视场角)、V FOV(垂直视场角),D FOV(对角视场角),如下图所示,一目了然。

图像的单应性变换
单应性的一个不严谨定义是:用无镜头畸变的相机从不同位置拍摄同一平面物体的图像之间存在单应性,可以用透视变换表示。

也就是说,给Right view的图像上的点经过透视变换可以变到left view图像上对应位置,透视变换也就是一个矩阵,我们称之为单应性矩阵。
这里不对单应性矩阵进行详细介绍,只是说求解单应性矩阵有8个参数,因此需要四组对应点。
一种常见的方法是寻找两张图像中的相似特征点,然后用来求解单应性矩阵,参考此链接中有相关代码,以及对单应性矩阵的具体介绍。
findHomography函数和getPerspectiveTransform函数
两个函数都可以用来求单应性矩阵,结果一样。但getPerspectiveTransform只会拿四组点去计算,findHomography会拿多组点(大于等于4组)点去计算。
参考链接
- https://danceswithcode.net/engineeringnotes/rotations_in_3d/rotations_in_3d_part1.html
- https://www.sohu.com/a/657116799_121116014
- https://zhuanlan.zhihu.com/p/74597564
- https://blog.csdn.net/Sunshine_in_Moon/article/details/45478351

![[答疑]张学友和Neal Ford的区别](https://img-blog.csdnimg.cn/img_convert/645c8520ee274d1379a38b9dccbc82f8.png)